А.Т.ФОМЕНКО
МАТЕМАТИКА И МИФ СКВОЗЬ ПРИЗМУ ГЕОМЕТРИИ

5. ОБРАЗЫ В ВАРИАЦИОННОМ ИСЧИСЛЕНИИ

МАТЕМАТИКА:
ЭТАП ДОКАЗАТЕЛЬСТВА ТЕОРЕМЫ СУЩЕСТВОВАНИЯ ГЛОБАЛЬНО МИНИМАЛЬНЫХ ПОВЕРХНОСТЕЙ

Минимальные поверхности - это поверхности наименьшей площади (или объема в многомерном случае).  Их физической моделью служат границы раздела двух физических сред, находящихся в равновесии. Например, мыльные пленки, затягивающие замкнутые проволочные контуры (когда их вынимают из мыльного раствора), являются минимальными поверхностями.  Известная гипотеза Плато в вариационном исчислении утверждает, что на любой "контур" всегда можно натянуть поверхность наименьшей площади. Или наименьшего объема, если речь идет о многомерных поверхностях. Для двумерных поверхностей эта проблема Плато была решена в первой половине ХХ века. Для общих многомерных поверхностей полное решение пока отсутствует. Однако доказаны глубокие теоремы, успешно решающие проблему Плато для специальных классов поверхностей.
Рисунок показывает один из центральных этапов в доказательстве многомерной проблемы Плато в классе так называемых "гомологических поверхностей". При минимизации площади (объема) поверхности может случиться, что из нее вырастают "тонкие усы". Они практически не влият на площадь (или объем) поверхности, однако существенно искажают ее метрические свойства и характер расположения поверхности в объемлющем пространстве.  Хорошо видно, что эти "усы" могут быть прихотливыми, и их появление может "испортить" минимизирующий процесс.  Чтобы этого не случилось, приходится "срезать", "сбривать усы". Аккуратное математическое оформление этой идеи и составляет один из самых нетривиальных моментов доказательства.

МИФОЛОГИЯ.
Атлант - титан, брат Прометея, отличавшийся огромной силой. После поражения титанов в последней битве с Зевсом, Атлант в наказание был вынужден поддерживать на своих плечах небесный свод на крайнем западе, вблизи сада Гесперид. Геракл добыл золотые яблоки из этого сада с помощью Атланта, который сходил за ними, переложив на Геракла свою ношу. Вернувшись, Атлант отказался снова взвалить на себя свод. Но был обманут Гераклом, попросившим Атланта хотя бы на время подержать свод, пока Геракл не сделает себе подушку, дабы смягчить тяжесть неба. По одной из версий Персей превратил Атланта в скалу, показав ему голову Горгоны.

МАТЕМАТИКА:
ДИСКРЕТНЫЕ ГРУППЫ, ПОРОЖДЕННЫЕ ОТРАЖЕНИЯМИ

Показана система "зеркал" в трехмерном пространстве, отражения относительно которых образуют дискретную группу. Этот класс групп (существующих и в многомерных пространствах) играет важную роль в геометрии, математической физике. Например, описание специального класса таких групп дает классификацию всех простых групп Ли. Так как каждое зеркало (т.е. гиперплоскость, проходящая через начало координат) однозначно задается своим вектором единичной нормали, то все свойства группы, порожденной отражениями, можно сформулировать в терминах векторов-нормалей к зеркалам. Интересны группы, порожденные отражениями в зеркалах, расположенных в многомерном пространстве Лобачевского. В некоторых случаях фактор-пространство пространства Лобачевского по действию такой группы является компактным гиперболическим многообразием конечного объема. Исследование таких многообразий - актуальная проблема современной гиперболической геометрии.

МИФОЛОГИЯ.
Якобы, среди "древне"-египетских храмов был "зеркальный храм", внутри которого все стены, потолки и т.п. были сделаны из зеркал. Он использовался для испытания жрецов. Под действием специального заклинания душа испытуемого покидала тело и начинала странствовать по храму, бесконечно отражаясь в тысячах зеркал. Обратный путь душа могла найти лишь в том случае, если боги решали, что она - чиста.
Другая ассоциация - райский сад, гигантский цветок в саду Эдема. В этом саду - фантастические растения, храмы, Золотой и Серебряный города.  Материалы, из которых выстроен Рай, светоносны. Они уподобляются то чистому золоту, то прозрачному стеклу, то кристаллам, то самоцветам.  Храм построен в виде цветка мандрагоры.  Считалось, что этот цветок хранит возбуждающую силу, вызывает любовное влечение. В то же время его называли "свечой дьявола" (якобы, светится по ночам в определенные дни), "цветком ведьмы". В средние века процветала индустрия изготовления поддельных мандрагоровых корней - важнейшей части растения.

МАТЕМАТИКА:
ТЕОРЕМА ПУАССОНА-ЛАПЛАСА И ПРИНЦИПЫ ПЛАТО

Двумерная поверхность, разделяющая две физические среды (например, газ-газ, газ-жидкость или жидкость-жидкость), называется поверхностью (границей) раздела сред. Если физическая система находится в равновесии, то известная теорема Пуассона-Лапласа утверждает, что поверхность раздела является поверхностью постоянной средней кривизны. При этом кривизна пропорциональна разности давлений в соприкасающихся средах.  Важный пример - это мыльные пузыри, и мыльные пленки. Или, более общо, мыльная пена, образующаяся при взбивании мыльного раствора. Соседние мыльные пузыри могут образовывать сингулярные ребра, стремясь вдавиться друг в друга. Ребра состоят из сингулярных точек мыльной поверхности. Они могут образовывать сложную пространственную структуру.  Согласно одному из принципов Плато, на одном сингулярном ребре могут (устойчиво) встречаться лишь три листа мыльной пленки. Причем листы встречаются под равными углами в 120 градусов. В сингулярной вершине могут сходиться лишь 4 сингулярных ребра. И тоже - под равными углами.

МИФОЛОГИЯ.
Извержение вулкана в океане. Взрыв раскаленного газа, разрастающиеся шары огня. Создание ада, геенны огненной. Данте зафиксировал одну из средневековых точек зрения, согласно которой в аду протекают реки античного аида, сливающиеся в единый поток. Он превращается в центре земли в громадное ледяное озеро Коцит. Харон - перевозчик душ умерших через реку Стикс. В самом центре ледяного озера (совпадающем с центром вселенной) в толщу льда вмерз Люцифер, верховный дьявол, терзающий "главных грешников". Вдали - пульсирующая огненная пасть, время от времени изрыгающая адское пламя. Эта живописная картина производила глубокое впечатление на людей.  Детали этой картины разрабатывались в поздне-средневековой литературе, живописи и богословии с исключительным вниманием.

МАТЕМАТИКА:
ПЛОЩАДЬ ПОВЕРХНОСТИ МОЖЕТ СТРЕМИТЬСЯ К НУЛЮ, А "ПРЕДЕЛ" ПОВЕРХНОСТИ МОЖЕТ СОВПАСТЬ СО ВСЕМ ПРОСТРАНСТВОМ

Поверхность, гомеоморфная двумерной сфере и расположенная в трехмерном пространстве, может деформироваться таким образом, что ее площадь стремится к нулю, однако "пределом" сферы будет все объемлющее пространство. При этом из сферы будут вытягиваться утончающиеся отростки-щупальца, площадь которых стремится к нулю, но их "длина", напротив, стремится к бесконечности.

МИФОЛОГИЯ.
Хуракан (Ураган) - "одноногий" - один из главных богов в мифологии киче. Творец и повелитель мира, владыка гроз, ветров и бурь. Простой смертный не может остаться в живых, если увидит "глаз Хуракана" ("глаз урагана").  Сторукие - это чудовища, порожденные богами Геей и Ураном.  Сторуких - трое. Это Котт, Бриарей и Гиес. У каждого из них по пятьдесят голов и сто рук. Сам Уран, ужаснувшись видом своих страшных потомков, погрузил их в недра земли. Отсюда они были вызваны лишь Зевсом, дабы помочь ему одержать победу над восставшими титанами. Поднявшиеся из-под земли сторукие сокрушили титанов. Затем снова погрузились в тартар, чтобы там охранять низверженных титанов. Сторукие внушают страх даже богам.  Например, когда Гера, Посейдон и Афина задумали заговор против Зевса, тому достаточно было лишь обратиться к сторуким. Один их вид шокировал противников Зевса и они поспешно ретировались.

МАТЕМАТИКА:
ПОЛИЭДРЫ И МАТРИЦЫ ИНЦИДЕНЦИЙ

В рисунке использованы разнообразные топологические объекты: полиэдры, особые точки поверхностей и т.п.

МИФОЛОГИЯ.
Из цикла "Трибунал". Судья зачитывает решение суда. Суд Христа или последний суд. Каждый человек призывается на суд и его судьба зависит от того - какая чаша весов перевесит: с добрыми или с плохими делами. Эти гигантские весы расположены сзади судей.

МАТЕМАТИКА:
ОРБИТА ДЕЙСТВИЯ БЕСКОНЕЧНОЙ ГРУППЫ

Говорят, что на пространстве задано действие группы, если ее элементы представлены как гомеоморфизмы пространства. Другими словами, задан мономорфизм группы в группу всех гомеоморфизмов пространства. Изображен важный объект, естественно связанный с такими действиями. А именно, - орбита данной группы.  Рассмотрим какую-либо область в пространстве, например, - ромбовидный полиэдр на рисунке.  Применим к ней все элементы бесконечной группы. В результате может получиться последовательность полиэдров, "повторяющих" друг друга. Это и есть орбита данного полиэдра при действии группы. Если полиэдр таков, что его образы "хорошим образом" покрывают все пространство (пересекаясь друг с другом лишь по границе), то его называют фундаментальной областью данной группы.

МИФОЛОГИЯ.
Скала Атлант, поддерживающая небесный свод на западе. Персей, показав голову Горгоны титану Атланту, превратил его в скалу. Превращение людей в камни - распространенный вид метаморфоз в мифах Южной Азии, Австралии, Океании, Южной Америки.  Люди превращаются в камни или в каменные изваяния либо в момент смерти, либо по приказу богов. Знаменитый греческий миф о Горгонах - чудовищных порождениях морских божеств Форкия и Кето. Две старшие сестры Горгоны - бессмертные, а младшая - Медуза - смертная. Обитают на крайнем западе рядом с Гесперидами, имеют ужасный вид: крылатые, с чешуей, со змеями вместо волос. Их взор обращает все живое в камень.  Персей победил Медузу лишь потому, что смотрел на ее отражение в своем зеркальном щите.  Считалось, что отраженный взгляд менее опасен, чем взгляд в упор.

МАТЕМАТИКА:
ГРАДИЕНТНЫЙ СПУСК

Изображена важная в вариационном исчислении операция "опускания цикла" вдоль интегральных траекторий градиентного векторного поля. При скольжении вниз цикл (который можно условно представлять в виде замкнутой поверхности) рано или поздно "зацепится" за критические точки функции (функционала) и повиснет на них. Нарисован цикл, повисший на двух критических точках. Они условно представлены в виде двух штырей, вбитых в блок.  Конечномерная теория Морса и ее разнообразные обобщения на бесконечномерный случай фактически изучают поведение циклов при таком "градиентном спуске".

МИФОЛОГИЯ.
"Усталость" - второе название этой работы.  Мифы Алтая сообщают, что первоначально было не одно солнце, а несколько.  Было настолько жарко, что некий охотник-лучник решил сбить стрелами все солнца, оставив только луну. Он успешно сбивает выстрелами из лука все солнца кроме последнего. Охотник промахивается. Последняя стрела ударяется в скалу, раскалывая ее сверху донизу. Охотник превращается в степного сурка - табаргана. По другой версии стрелок был по горло зарыт в землю, или даже под землю. Поскольку дерзнул состязаться в стрельбе с самим богом. В результате проиграл. Тем не менее охотник и поныне продолжает свое опасное занятие. Причем, его подземные стрелы страшнее небесных, так как стрелы охотника - это чума.

МАТЕМАТИКА:
ОРИЕНТИРУЕМОСТЬ И НЕОРИЕНТИРУЕМОСТЬ МНОГООБРАЗИЙ

Изображена цепочка фигур, каждая из которых держит в руках раскаленный шар. Цепочка образует замкнутую петлю. Если на многообразии нарисовать замкнутый непрерывный путь, то можно "протащить" вдоль него репер, то есть набор касательных векторов, образующих базис в касательной плоскости. Если репер вернется в исходную точку с противоположной ориентацией, значит многообразие неориентируемо. Задание репера эквивалентно заданию ориентации шара малого радиуса, лежащего в многообразии.  Другими словами, вместо непрерывной деформации репера вдоль пути можно "прокатить" шар. А затем сравнить его исходную ориентацию с той, какая появится на нем после однократного обхода петли.

МИФОЛОГИЯ.
Древний обряд магического управления солнцем для прекращения засухи. Весь народ выстраивался в длинную шеренгу, причем каждый держал зеркало или полированный (зеркальный) шар. Считалось, что отраженные зеркалами лучи возвратятся к солнцу и оно ослепнет на время и прекратит сжигать страну. Жрец руководил ритуалом.

МАТЕМАТИКА:
2-АДИЧЕСКИЙ СОЛЕНОИД

Этот объект известен в топологии не только как обладающий интересными свойствами, но и позволяющий проверять разнообразные гипотезы в геометрии. Соленоид - хороший "тест". Его конструкция проста. Нужно взять полноторие, т.е. прямое произведение диска на окружность, или "заполненный тор", бублик.  Затем следует взять второе полноторие и вложить его в первое как показано на рисунке. То есть, "намотав" два раза вдоль оси первого полнотория. В результате второе полноторие расположится внутри первого, как змея, свернувшаяся в два кольца.  На следующем шаге нужно взять третье полноторие и вложить его во второе, намотав два раза вдоль оси второго полнотория. В результате третье полноторие намотается 4 раза вдоль оси первого.  Продолжая, получаем бесконечную последовательность вложенных полноторий.  Можно рассмотреть "их предел". Получающееся "предельное пространство" и называется 2-адическим соленоидом.  На рисунке изображена последовательность граничных торов этих полноторий вплоть до тора с номером IX.  Часть поверхности каждого тора удалена (т.е. торы разрезаны), чтобы можно было видеть их внутренность.  Интерес к этому объекту возрос в последнее время, когда обнаружилось, что такая "2-адическая намотка" торов естественно появляется в гамильтоновой и симплектической топологии.  Здесь в качестве торов выступают так называемые торы Лиувилля.  Оказалось, что такие "двукратные намотки торов" описывают важные свойства интегрируемых дифференциальных уравнений.

МИФОЛОГИЯ.
Зме'й или змея - один из основных мифологических образов многих древних культов. Распространен образ змеи, проглатывающей саму себя, т.е. заглатывающей свой хвост. В германской мифологии змей-червь - главное воплощение космического зла. Играет основную роль в предстоящей гибели мира.  Аналогично, в "древне"-египетской мифологии прабожество Атум в конце мира должно вернуться в виде злой змеи Урей в первичный хаос, из которого оно некогда возникло. Часто змея изображается свернутой в несколько колец, которые сложным образом перепутываются. Один из способов древнего гадания - по форме колец и узлов отдыхающей змеи.

МАТЕМАТИКА:
ЭЛЕМЕНТЫ ТОПОЛОГИИ МНОГООБРАЗИЙ. I

Юмористические сценки из жизни двумерных и трехмерных многообразий. В частности, показаны операции Дена - "скручивания". Шар с "ушками". Рояль с цветком.

МАТЕМАТИКА:
ЭЛЕМЕНТЫ ТОПОЛОГИИ МНОГООБРАЗИЙ. II

Юмористические сценки из жизни двумерных и трехмерных многообразий. Перестройки торов Лиувилля в интегрируемых системах. "Атомы" типа В.

МАТЕМАТИКА:
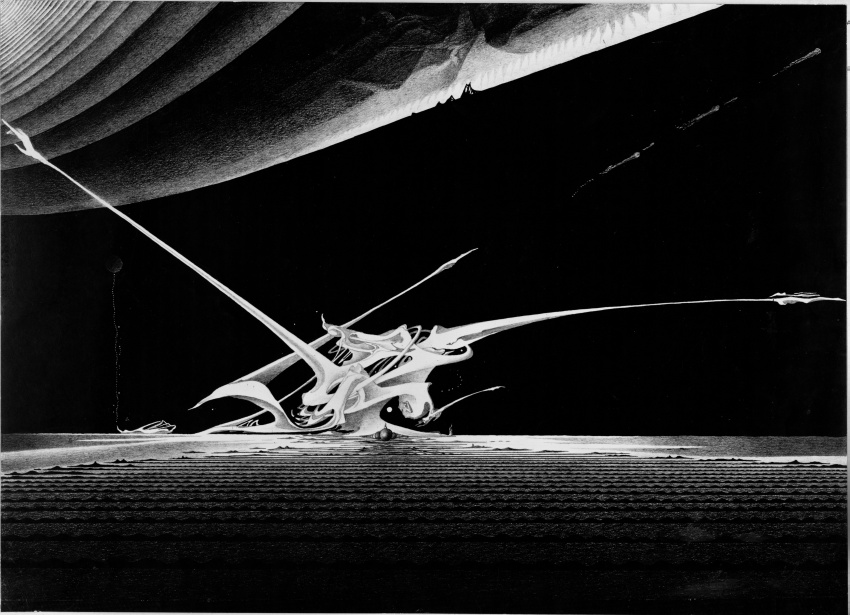
ПРОСТРАНСТВЕННАЯ ЗАДАЧА МНОГИХ ТЕЛ В НЕБЕСНОЙ МЕХАНИКЕ

В первом приближении считается, что планеты солнечной системы, астероиды и т.п. движутся в одной плоскости, называемой плоскостью эклиптики. Центр масс всей системы можно считать совмещенным с Солнцем. Движение системы управляется ньютоновским потенциалом, согласно законам классической механики.  Эволюция системы определяется начальными данными.  Надо задать положения гравитирующих масс и их скорости в начальный момент времени. Общие решения такой системы уравнений сложны. Еще более сложна задача описания движения многих тел, движущихся в трехмерном пространстве, но не обязательно расположенных в одной плоскости (под влиянием потенциала общего вида).  На рисунке каждое твердое тело условно изображено в виде птицы, парящей не по собственному желанию, а в соответствии со взаимным притяжением со стороны других "птиц".  Вся система вращается вокруг общего центра масс.  Некоторые тела могут удаляться от него, а некоторые - приближаться, или даже "падать" на центр масс.  Задача многих тел является одной из самых интересных задач. Здесь встречаются такие области знания, как геометрия, небесная механика, дифференциальные уравнения.

МИФОЛОГИЯ.
Гарпии, во'роны, гаруды. Гарпии - архаические доолимпийские божества - крылатые дикие женщины-полуптицы безобразного вида. В мифологии Греции - похитительницы детей и человеческих душ, внезапно налетающие и так же стремительно исчезающие. Связаны с ветрами и бурями. Гаруды в буддийской мифологии - огромные птицы, крылья которых порождают ураган.  Иногда гаруды принимают человеческий облик. Во'роны связаны с царством мертвых, с жестоким битвами. Часто выступают как мудрые птицы, но всегда как вестники зла. В средневековой христианской традиции во'рон - олицетворение сил ада и дьявола.  Умение во'рона подражать человеческой речи породило представление о нем как о вестнике богов.