Глава 1.
НЕКОТОРЫЕ НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ АСТРОНОМИИ И ИСТОРИИ АСТРОНОМИИ
1. ЭКЛИПТИКА, ЭКВАТОР, ПРЕЦЕССИЯ.
Рассмотрим движение Земли по орбите вокруг Солнца. Обычно считается, что вокруг Солнца движется не сама Земля, а центр масс (центр тяжести) системы Земля-Луна, так называемый барицентр. Барицентр находится недалеко от центра Земли, по сравнению с расстоянием до Солнца. Для целей настоящей книги можно считать, что орбитальное движение барицентра вокруг Солнца отождествляется с движением Земли вокруг Солнца.
Гравитационные возмущения от планет вызывают непрерывный поворот плоскости орбиты барицентра. Это вращение имеет некоторую основную синусоидальную составляющую с очень большим периодом. На главную составляющую накладываются некоторые малые переменные колебания, которыми мы будем пренебрегать. Эта вращающаяся плоскость орбиты Земли и называется плоскостью эклиптики.
Иногда эклиптикой называется окружность пересечения плоскости эклиптики с воображаемой сферой неподвижных звезд. За центр этой сферы условно примем центр Земли, лежащий в плоскости эклиптики. На рис.1.1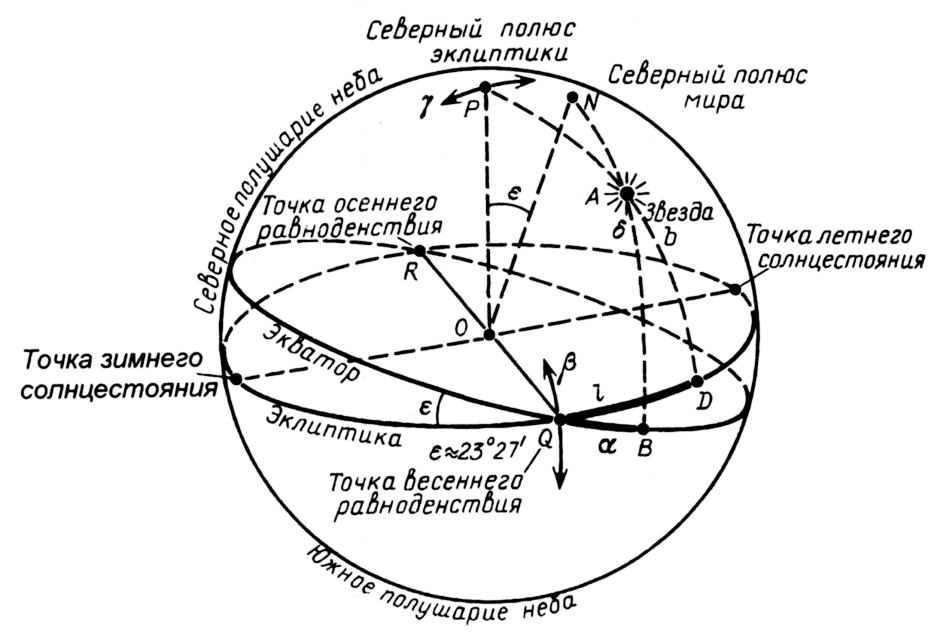 это точка O. По отношению к далеким звездам движением Земли можно пренебречь и считать ее неподвижным центром звездной сферы. В дальнейшем, говоря о каком-либо небесном объекте -- Солнце, звезде и т.п., будем отождествлять с ним точку его проекции на сферу неподвижных звезд.
это точка O. По отношению к далеким звездам движением Земли можно пренебречь и считать ее неподвижным центром звездной сферы. В дальнейшем, говоря о каком-либо небесном объекте -- Солнце, звезде и т.п., будем отождествлять с ним точку его проекции на сферу неподвижных звезд.
Эклиптика вращается со временем, поэтому ее называют подвижной эклиптикой. Чтобы охарактеризовать положение подвижной эклиптики в каждый момент времени, вводится понятие мгновенной эклиптики, для данного года или для данной эпохи. Понятие и свойства мгновенного вектора угловой скорости и мгновенной эклиптики изучаются в рамках небесной механики. Фиксированные последовательные мгновенные эклиптики для разных эпох иногда называются неподвижными эклиптиками этих эпох. Например, удобно говорить о неподвижной эклиптике 1 января 1900 года. Положение подвижной эклиптики на любой момент времени можно задавать относительно одной из неподвижных эклиптик, произвольно выбранной.
В небесной механике Земля считается абсолютно твердым телом. Хорошо известно, что твердое тело обладает так называемым эллипсоидом инерции, который однозначно задается своими тремя полуосями. Вращение твердого тела характеризуется величиной и положением в пространстве вектора угловой скорости вращения ω. Вектор ω иногда называется мгновенной осью вращения. Полуоси эллипсоида инерции ортогональны, поэтому их можно взять в качестве ортогональной системы координат. Тогда вектор ω можно задать проекциями x, y, z на оси инерции. Моменты инерции тела относительно этих осей обозначим A, B, C соответственно. Вращение твердого тела описывается динамическими уравнениями Эйлера-Пуассона
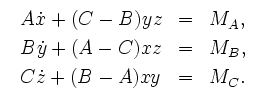
В правой части уравнений стоят проекции на те же оси инерции вектора M, называемого моментом внешних сил относительно центра масс твердого тела. Момент M возникает, в основном, благодаря действию притяжения Луны и Солнца на эллипсоидальную фигуру Земли. Обычно Землю считают не трехосным, а двухосным эллипсоидом, то есть эллипсоидом вращения.
Положение вектора M относительно осей инерции меняется быстро и сложно, однако, используя современные теории движения Земли и Луны, его эволюцию можно вычислить с достаточной точностью для любого момента времени. Следовательно, можно решить уравнение Эйлера-Пуассона, то есть вычислить эволюцию вектора ω.
Для учета всех нерегулярностей в движении Земли пользуются "Таблицами движения Земли вокруг Солнца" известного астронома С.Ньюкомба [1295].
Исследование тех случаев (конфигураций твердого тела), когда уравнения Эйлера-Пуассона решаются точно, составляет важный раздел современной теоретической механики, физики, геометрии.
Рассмотрим вектор ω мгновенного вращения Земли. Он задает ось вращения, то есть мгновенную ось вращения. Точки ее пересечения с земной поверхностью называются мгновенными полюсами Земли, а точки пересечения с небесной сферой, то есть со сферой неподвижных звезд, называются полюсами мира -- северным и южным. Рассмотрим плоскость, ортогональную оси мгновенного вращения Земли и проходящую через центр масс Земли. Ее пересечение с земной поверхностью называется мгновенным экватором вращения Земли, а пересечение с небесной сферой -- истинным небесным экватором, или просто небесным экватором, или еще проще -- экватором.
На рис.1.1 изображена небесная сфера с центром O, северным полюсом эклиптики P и полюсом мира N. Эклиптика и экватор пересекаются в двух точках, которые называются точками весеннего и осеннего равноденствий и обозначены на рис.1.1
изображена небесная сфера с центром O, северным полюсом эклиптики P и полюсом мира N. Эклиптика и экватор пересекаются в двух точках, которые называются точками весеннего и осеннего равноденствий и обозначены на рис.1.1 буквами Q и R. На рисунке иллюстрируется также измерение координат звезды относительно двух систем координат на небесной сфере -- экваториальной и эклиптикальной.
буквами Q и R. На рисунке иллюстрируется также измерение координат звезды относительно двух систем координат на небесной сфере -- экваториальной и эклиптикальной.
Рассмотрим теперь систему координат, не вращающуюся вместе с Землей, а связанную, например, с эклиптикой. При этом новая система координат не обязана быть ортогональной. В качестве осей такой системы координат берут обычно следующие:
1) нормаль к плоскости эклиптики;
2) ось пересечения плоскости эклиптики и плоскости экватора, то есть ось равноденствия;
3) ось инерции C.
Проекции вектора ω мгновенной угловой скорости на эти три оси обозначаются через 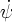

 . Таким образом, мы разложили скорость вращения Земли на три составляющие. Каков их геометрический смысл? Величина
. Таким образом, мы разложили скорость вращения Земли на три составляющие. Каков их геометрический смысл? Величина 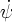 называется скоростью прецессии Земли. Под влиянием этой составляющей, ось прецессии C, -- то есть третья ось инерции, - перемещается вокруг нормали OP по круговому конусу, рис.1.2
называется скоростью прецессии Земли. Под влиянием этой составляющей, ось прецессии C, -- то есть третья ось инерции, - перемещается вокруг нормали OP по круговому конусу, рис.1.2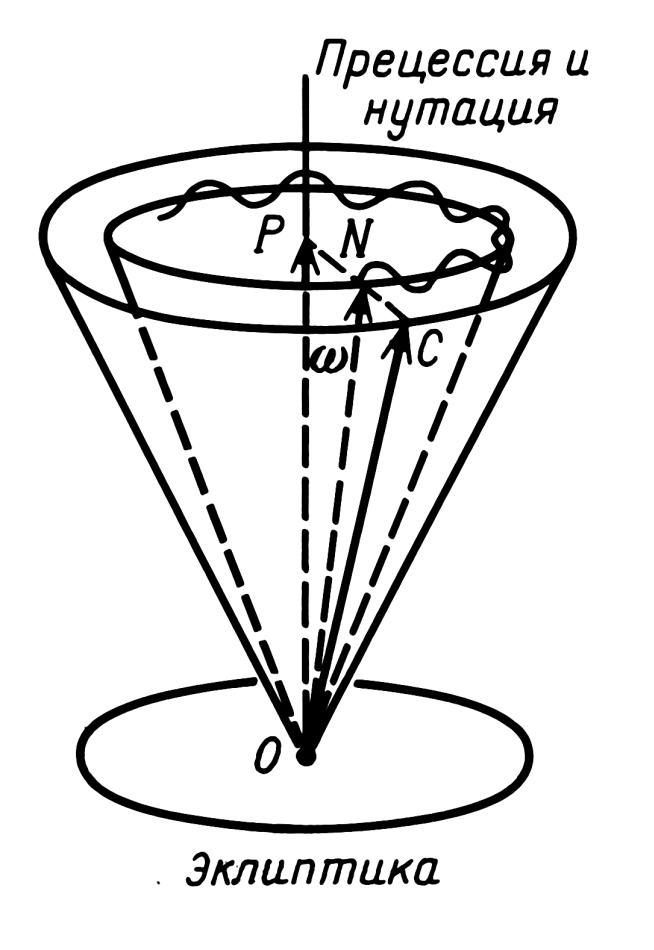 . Вслед за ней перемещается по конусу и вектор ω = ON. Отметим, что векторы ω и OC весьма близки. При расчетах, не требующих чрезвычайной точности, можно считать, что вектор ω совпадает с осью OC.
. Вслед за ней перемещается по конусу и вектор ω = ON. Отметим, что векторы ω и OC весьма близки. При расчетах, не требующих чрезвычайной точности, можно считать, что вектор ω совпадает с осью OC.
Вследствие прецессии, ось равноденствия, -- то есть прямая пересечения эклиптики и экватора, -- вращается в плоскости эклиптики. Результатом вращения  является некоторое изменение угла наклона оси OC к эклиптике. Наконец, величина
является некоторое изменение угла наклона оси OC к эклиптике. Наконец, величина  определяет скорость вращения Земли вокруг оси OC. В теоретической механике величина
определяет скорость вращения Земли вокруг оси OC. В теоретической механике величина  называется скоростью собственного вращения. Она существенно больше угловых скоростей
называется скоростью собственного вращения. Она существенно больше угловых скоростей 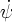 и
и  . С точки зрения теоретической механики это обстоятельство является отражением того, что устойчивое вращение твердого тела происходит вокруг оси, близкой к оси наибольшего момента инерции, то есть вокруг наименьшей оси эллипсоида инерции. Напомним, что Земля слегка сплюснута с полюсов.
. С точки зрения теоретической механики это обстоятельство является отражением того, что устойчивое вращение твердого тела происходит вокруг оси, близкой к оси наибольшего момента инерции, то есть вокруг наименьшей оси эллипсоида инерции. Напомним, что Земля слегка сплюснута с полюсов.
Итак, ω= 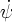 +
+  +
+  , где знаком "+" обозначена сумма векторов. Каждая из скоростей
, где знаком "+" обозначена сумма векторов. Каждая из скоростей 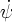 ,
,  ,
,  содержит одну постоянную (или почти постоянную) составляющую и сумму большого числа небольших периодических членов, называемых нутациями. Пренебрегая ими, получаем следующую картину вращения Земли.
содержит одну постоянную (или почти постоянную) составляющую и сумму большого числа небольших периодических членов, называемых нутациями. Пренебрегая ими, получаем следующую картину вращения Земли.
1. Постоянная составляющая скорости 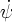 называется прецессией в долготе. Она равномерно перемещает ось OC по круговому конусу со скоростью примерно 50'' в год, рис.1.2
называется прецессией в долготе. Она равномерно перемещает ось OC по круговому конусу со скоростью примерно 50'' в год, рис.1.2 . При этом ось равноденствия вращается по эклиптике по часовой стрелке, если смотреть со стороны северного полюса эклиптики. Вектор прецессии направлен к южному полюсу эклиптики.
. При этом ось равноденствия вращается по эклиптике по часовой стрелке, если смотреть со стороны северного полюса эклиптики. Вектор прецессии направлен к южному полюсу эклиптики.
2. Постоянная составляющая скорости  сегодня приблизительно равна 0,5" в год.
сегодня приблизительно равна 0,5" в год.
3. Постоянная составляющая скорости  -- это среднее собственное вращение Земли с периодом в одни сутки вокруг оси OC против часовой стрелки, если смотреть с северного полюса Земли.
-- это среднее собственное вращение Земли с периодом в одни сутки вокруг оси OC против часовой стрелки, если смотреть с северного полюса Земли.
Отметим, что ось OP -- нормаль к плоскости эклиптики, вектор ω -- мгновенная угловая скорость Земли, и ось OC -- третья ось инерции, лежат в одной плоскости. Прецессия поворачивает эту плоскость вокруг оси OP.
Нутационные члены в скоростях 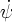 ,
,  ,
,  искажают описанную выше картину вращения. Поэтому вектор ω движется в пространстве не по идеальному конусу, а по "волнистой" поверхности, все время находящейся около конуса. На рис.1.2
искажают описанную выше картину вращения. Поэтому вектор ω движется в пространстве не по идеальному конусу, а по "волнистой" поверхности, все время находящейся около конуса. На рис.1.2 траектория, прочерчиваемая концом вектора ω, изображена волнистой линией.
траектория, прочерчиваемая концом вектора ω, изображена волнистой линией.
Две окружности, лежащие на небесной сфере, -- эклиптика и экватор - пересекаются под углом 
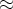 23o27' в двух точках Q и R, рис.1.1
23o27' в двух точках Q и R, рис.1.1 . Солнце в своем годичном движении вдоль эклиптики два раза пересекает экватор в этих точках. Точка Q, в которой Солнце в своем движении переходит в северное полушарие, называется точкой весеннего равноденствия. В этот момент длительности дня и ночи совпадают в каждой точке земной поверхности. Точка R -- это точка осеннего равноденствия, рис.1.1
. Солнце в своем годичном движении вдоль эклиптики два раза пересекает экватор в этих точках. Точка Q, в которой Солнце в своем движении переходит в северное полушарие, называется точкой весеннего равноденствия. В этот момент длительности дня и ночи совпадают в каждой точке земной поверхности. Точка R -- это точка осеннего равноденствия, рис.1.1 .
.
Подвижная эклиптика постепенно поворачивается. Поэтому точка весеннего равноденствия постепенно перемещается вдоль экватора, одновременно смещаясь и вдоль эклиптики. Скорость смещения точки равноденствия вдоль эклиптики и есть прецессия в долготе. Смещение точек равноденствия вызывает "предварение равноденствий", рис.1.1 .
.
2. ЭКВАТОРИАЛЬНЫЕ И ЭКЛИПТИКАЛЬНЫЕ КООРДИНАТЫ.
Для записи наблюдений небесных светил нужны какие-либо удобные координаты, позволяющие фиксировать положения небесных объектов относительно друг друга. Существует несколько таких систем координат. Прежде всего, это экваториальные координаты, задаваемые следующим образом.
На рис.1.1 отмечены северный полюс N и небесный экватор, содержащий дугу QB. Можно считать, что с достаточной для нас точностью плоскость небесного экватора совпадает с плоскостью земного экватора. При этом мы считаем, что центр Земли помещен в точку O - центр небесной сферы. Точка Q -- это точка весеннего равноденствия. Пусть точка A изображает произвольную неподвижную звезду. Рассмотрим меридиан NB, проходящий через северный полюс и звезду A. Точка B -- точка пересечения меридиана с плоскостью экватора. Дуга QB = α изображает экваториальную долготу звезды A. Эта долгота называется также прямым восхождением. Дуга отсчитывается в сторону, противоположную направлению движения точки весеннего равноденствия Q. Следовательно, с течением времени в силу прецессии прямые восхождения звезд медленно увеличиваются.
отмечены северный полюс N и небесный экватор, содержащий дугу QB. Можно считать, что с достаточной для нас точностью плоскость небесного экватора совпадает с плоскостью земного экватора. При этом мы считаем, что центр Земли помещен в точку O - центр небесной сферы. Точка Q -- это точка весеннего равноденствия. Пусть точка A изображает произвольную неподвижную звезду. Рассмотрим меридиан NB, проходящий через северный полюс и звезду A. Точка B -- точка пересечения меридиана с плоскостью экватора. Дуга QB = α изображает экваториальную долготу звезды A. Эта долгота называется также прямым восхождением. Дуга отсчитывается в сторону, противоположную направлению движения точки весеннего равноденствия Q. Следовательно, с течением времени в силу прецессии прямые восхождения звезд медленно увеличиваются.
Дуга меридиана AB= δ изображает на рис.1.1 экваториальную широту звезды A, называемую также склонением звезды A. Если пренебречь колебаниями эклиптики, то склонения звезд, расположенных в северном полушарии, с течением времени медленно уменьшаются, из-за смещения точки весеннего равноденствия Q. При этом склонения звезд, расположенных в южном полушарии, медленно увеличиваются.
экваториальную широту звезды A, называемую также склонением звезды A. Если пренебречь колебаниями эклиптики, то склонения звезд, расположенных в северном полушарии, с течением времени медленно уменьшаются, из-за смещения точки весеннего равноденствия Q. При этом склонения звезд, расположенных в южном полушарии, медленно увеличиваются.
При суточном движении Земли склонения звезд не меняются, а прямые восхождения равномерно изменяются, со скоростью вращения Земли.
Другой часто используемой системой, особенно в древних звездных каталогах, является эклиптикальная, или эклиптическая система координат.
Рассмотрим небесный меридиан, проходящий через полюс эклиптики P и через звезду A, рис.1.1 . Он пересекает плоскость эклиптики в точке D. Дуга QD изображает на рис.1.1
. Он пересекает плоскость эклиптики в точке D. Дуга QD изображает на рис.1.1 эклиптикальную или эклиптическую долготу l, а дуга AD -- эклиптикальную широту b. С течением времени в силу прецессии дуга QD увеличивается, примерно на 1 градус за 70 лет. Следовательно, эклиптикальные долготы со временем равномерно возрастают.
эклиптикальную или эклиптическую долготу l, а дуга AD -- эклиптикальную широту b. С течением времени в силу прецессии дуга QD увеличивается, примерно на 1 градус за 70 лет. Следовательно, эклиптикальные долготы со временем равномерно возрастают.
Если пренебречь колебаниями эклиптики, то в первом приближении можно считать, что эклиптикальные широты b не меняются со временем. Именно это обстоятельство сделало эклиптикальные координаты популярными среди средневековых астрономов. Преимущество эклиптикальных координат по сравнению с экваториальными заключается в том, что вследствие прецессии величина l равномерно увеличивается, а величина b постоянна. Изменения же экваториальных координат вследствие прецессии происходят по существенно более сложным формулам, учитывающим ортогональный поворот эклиптики, совмещающий ее с экватором.
Именно поэтому средневековые астрономы стремились составлять свои каталоги в эклиптикальных координатах. Хотя из наблюдений легче найти экваториальные координаты, поскольку их нахождение не требует определения плоскости эклиптики. Положение эклиптики связано с движением Земли вокруг Солнца и требует для своего определения нетривиальных методов, влекущих за собой дополнительные систематические ошибки в координатах всех звезд. Открытие того факта, что эклиптика колеблется со временем, привело к тому, что в звездных каталогах стали приводить не эклиптикальные, а экваториальные координаты звезд. Так это делается и сегодня. "Преимущество" эклиптикальных координат исчезло.
3. СПОСОБЫ ИЗМЕРЕНИЯ ЭКВАТОРИАЛЬНЫХ И ЭКЛИПТИКАЛЬНЫХ КООРДИНАТ.
Вкратце остановимся на конкретных способах измерения экваториальных и эклиптикальных координат. Мы опишем простую геометрическую идею, лежащую в основе таких измерительных приборов, как квадрант, секстант, меридианный круг и др.
Пусть наблюдатель H находится на поверхности Земли на широте φ. См. рис.1.3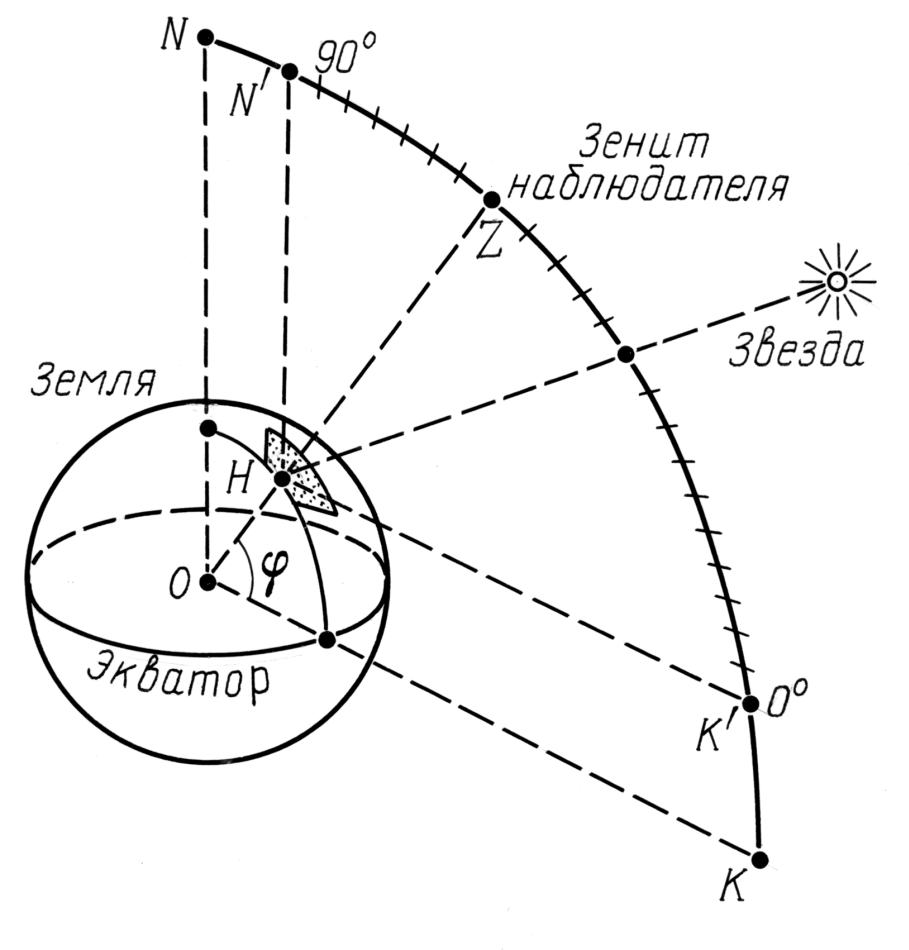 и рис.1.4
и рис.1.4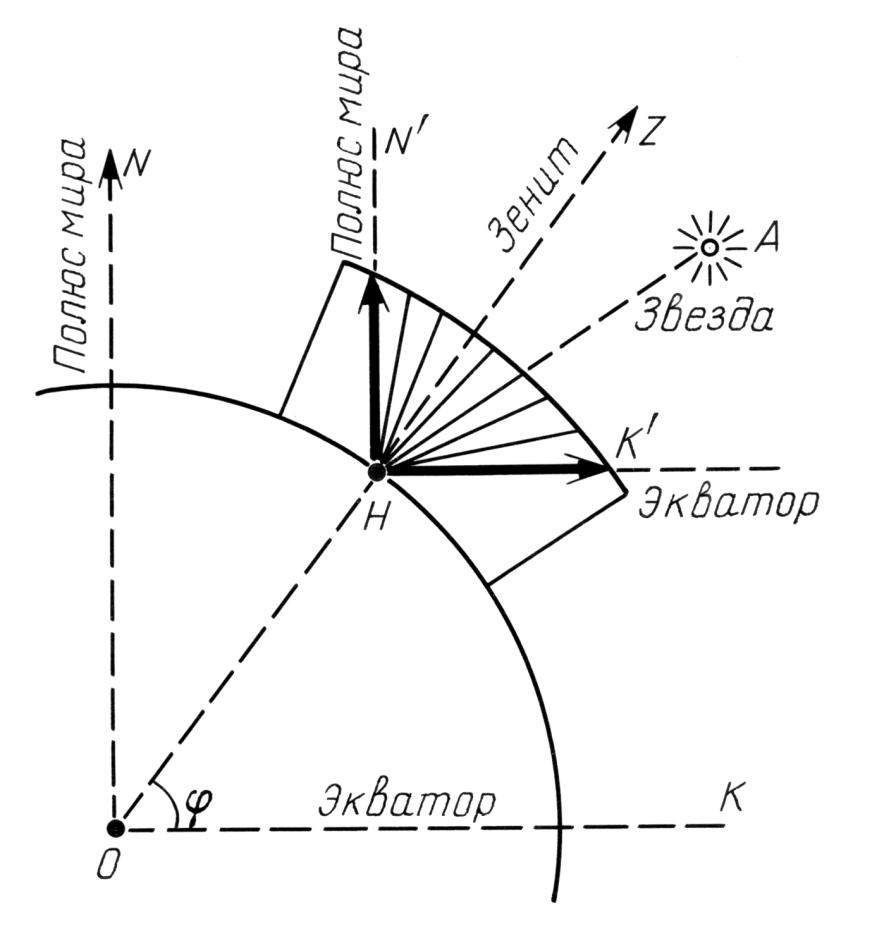 . Достаточно легко определить прямую HN', направленную на северный полюс мира и параллельную ON. Далее, надо определить меридиан, проходящий через точку H, и установить на поверхности Земли вертикальную стенку, направленную вдоль этого меридиана, рис.1.3
. Достаточно легко определить прямую HN', направленную на северный полюс мира и параллельную ON. Далее, надо определить меридиан, проходящий через точку H, и установить на поверхности Земли вертикальную стенку, направленную вдоль этого меридиана, рис.1.3 и рис.1.4
и рис.1.4 . Отмечая на ней направление HN' на полюс мира, мы можем отметить также линию экватора HK', параллельную OK, отложив угол
. Отмечая на ней направление HN' на полюс мира, мы можем отметить также линию экватора HK', параллельную OK, отложив угол ![]() от направления HN'. Прямой угол N'HK' делится на градусы. В результате получается угломерный астрономический прибор: четверть разделенного круга, расположенная в вертикальной плоскости (по отвесу). Основа этого прибора заложена в меридианных инструментах. С его помощью можно измерять склонения звезд, то есть их экваториальные широты, а также отмечать моменты прохождения звезд через меридиан, через так называемый вертикал.
от направления HN'. Прямой угол N'HK' делится на градусы. В результате получается угломерный астрономический прибор: четверть разделенного круга, расположенная в вертикальной плоскости (по отвесу). Основа этого прибора заложена в меридианных инструментах. С его помощью можно измерять склонения звезд, то есть их экваториальные широты, а также отмечать моменты прохождения звезд через меридиан, через так называемый вертикал.
Из серии независимых наблюдений можно с высокой точностью определить плоскость экватора на данной широте. Поэтому склонения можно измерять достаточно точно. В то же время, как видно из описанной элементарной небесной механики, измерение долгот требует фиксации моментов прохождения звезд через меридиан. Для этого нужны либо достаточно точные часы, либо дополнительный прибор, позволяющий быстро измерить расстояние по долготе между интересующей нас звездой и фиксированным меридианом. В любом случае измерение долгот является существенно более тонкой операцией. Поэтому следует ожидать, что средневековые астрономы должны были определять прямые восхождения более грубо, чем склонения.
Для определения эклиптикальных координат звезд наблюдатель H должен сначала определить положение на небе эклиптики. Это весьма непросто и требует хорошего понимания геометрических элементов в движении Земли и Солнца. Древние способы определения угла наклона эклиптики к экватору и положения оси равноденствия при помощи армиллярной сферы или астролябии описаны, в частности, в [614]. Важно отметить, что непосредственно измерять эклиптикальные координаты серии звезд можно лишь при помощи того или иного часового механизма, который позволял бы компенсировать суточное вращение Земли и удерживать постоянным направление на точку равноденствия. Очевидная трудность решения этой задачи приводила к тому, что при реальном вычислении эклиптикальных координат астрономы пользовались либо формулами поворота небесной сферы, либо небесными глобусами, на которые наносилась сетка как экваториальных, так и эклиптикальных координат. После этого, зная экваториальные координаты, можно было вычислить эклиптикальные. Естественно, возникали неизбежные ошибки, связанные с неточностью определения положения эклиптики по отношению к экватору и положения оси равноденствия.
Из этого краткого обсуждения способов измерения эклиптикальных координат следует, что, вероятнее всего, средневековыми астрономами использовался следующий алгоритм.
1) Определялись экваториальные координаты, причем, широты -- с большей точностью, чем долготы.
2) Вычислялось положение эклиптики и оси равноденствия по отношению к экватору.
3) Затем при помощи инструмента или тригонометрических формул, или же на небесном глобусе с двойной сеткой координат, экваториальные координаты пересчитывались в эклиптикальные.
Более того, поскольку все старинные наблюдательные инструменты были связаны с земной поверхностью, -- попросту говоря, установлены тем или иным способом на земле, -- то описанный алгоритм является единственным реальным способом определения эклиптикальных координат звезд. Тот факт, что наблюдательный инструмент закреплен на земной поверхности и, тем самым, участвует в суточном вращении Земли, означает, что этот инструмент изначально связан с экваториальной системой координат.
Ниже, в результате статистической обработки каталога Альмагеста, мы получим подтверждение описанного выше алгоритма, то есть, приведем аргументы в пользу того, что составитель Альмагеста пользовался именно этим приемом, или эквивалентным ему.