Глава 5.
АНАЛИЗ СИСТЕМАТИЧЕСКИХ ОШИБОК ЗВЕЗДНОГО КАТАЛОГА.
0. ОСНОВНАЯ ИДЕЯ.
0.1. НАГЛЯДНАЯ АНАЛОГИЯ.
Необходимость анализа ошибок звездного каталога нами разъяснена ранее. Мы, разумеется, прежде всего имеем в виду Альмагест, но излагаемый метод будет применяться и к другим реальным и искусственно генерируемым каталогам. В этой главе будет показано, как обнаруживать и компенсировать систематическую ошибку. Идея метода проста и естественна. Более того, он в той или иной форме давно уже используется в математической статистике. Чтобы пояснить его идею, рассмотрим следующий пример. Пусть мы рассматриваем результаты стрельбы в тире, которые показаны на рисунке.
Точками изображены следы от пуль. Спрашивается, какова точность попадания? Ответ очевиден: плохая. Однако, мы видим, что так называемая кучность достаточно хорошая. Это заставляет предположить, что сам стрелок хороший, а то обстоятельство, что все пули попали в сторону от "яблочка" может быть объяснено, например, тем, что прицел установлен неправильно. Разумеется, выяснить, вследствие чего произошло такое смещение, не видя винтовки, нельзя, но определить величину смещения можно. Разумный способ сделать это -- определить геометрический центр всех результатов и провести вектор из центра яблочка в найденный центр. На рис.5a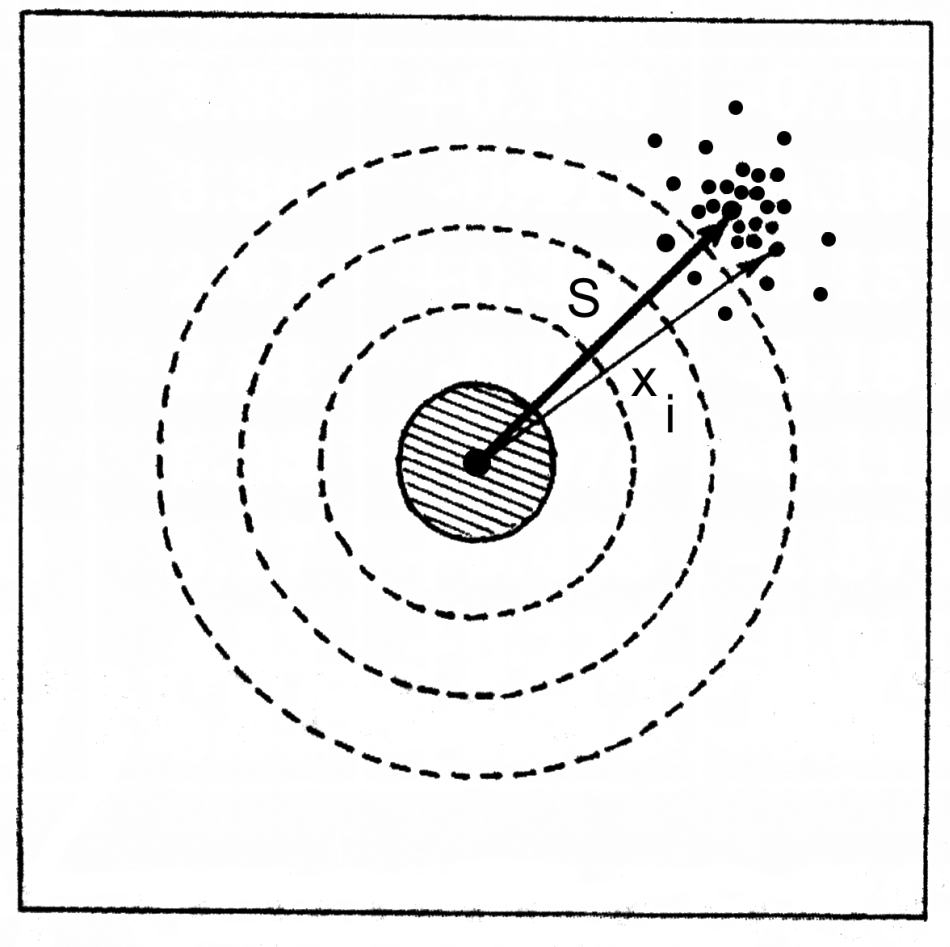 
- это вектор S. Как формально получить вектор S? Очень просто. Нужно взять векторы xi, соответствующие i-му результату стрельбы, и усреднить их по общему количеству N выстрелов:
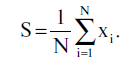
Отметим также, что вектор S альтернативно можно вычислить из задачи минимизации среднеквадратичного отклонения: найти вектор S, при котором достигается минимум функции
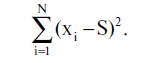
Здесь мы приняли, что (xi - S)2 = (xi1 - S1)2 + (xi2 - S2)2, где xi1, xi2 и (S1, S2) -- координаты векторов xi и S соответственно.
Тогда точность самого' стрелка можно охарактеризовать разбросом результатов вокруг найденного центра, что существенно выше точности попадания в яблочко. В нахождении вектора S и заключается в данном примере компенсация систематической ошибки. Собственно, S ее и представляет.
Формально, если мы изменим систему координат, сместив ее начало из центра яблочка на вектор S, то результаты стрельбы в новой системе координат будут содержать лишь случайные составляющие (вызванные дрожанием рук и т.п.) и не будут содержать регулярной составляющей.
Теперь вернемся к звездному каталогу. Мы хотим проверить, существует ли систематическая ошибка в какой-то его части и, если существует, определить ее. Пусть сначала не стоит проблема датировки, то есть мы наверняка знаем дату составления каталога tA (здесь "A", конечно же, означает Альмагест, но все рассуждения верны и для любых других каталогов). Тогда нужно сравнить истинные координаты звезд на момент tA (известные из современных точных каталогов) со значениями координат из изучаемого каталога, относящиеся к исследуемой его части. При этом сравнении, как и в примере с мишенью, нужно найти среднее отклонение сравниваемых координат. Пусть общее число звезд в избранной области равно N. Обозначим через li и Li соответственно эклиптикальную долготу i-й звезды в изучаемом каталоге и точное значение ее долготы. Аналогично, обозначим bi и Bi эклиптикальные широты i-й звезды (в каталоге и точное значение). Тогда средняя (систематическая) ошибка по долготе равняется
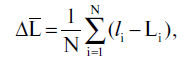
а систематическая ошибка по широте
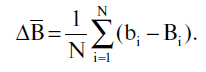
Эти ошибки, как уже сказано, могли произойти из-за неправильного определения плоскости эклиптики и ряда других, вообще говоря, неизвестных нам причин. Причины мы так и не выявим (впрочем, сделаем некоторые предположения на их счет), а вот ошибку, вызванную ими, скомпенсируем. Для этого нужно, попросту, изменить систему координат каталога (аналогично тому, как мы это сделали в примере с мишенью) так, чтобы результирующие средние долготные и широтные ошибки равнялись нулю.
0.2. РЕАЛИЗАЦИЯ МЕТОДА.
В данном пункте мы покажем, как конкретно реализуется общая идея, описанная выше.
Прежде всего, отметим, что мы будем компенсировать только широтную ошибку. Причины тому названы ранее и мы лишь упомянем здесь, что это позволяет уменьшить ошибку расчетов, что существенно ввиду низкой точности древних каталогов.
Итак, у нас есть каталог, из которого мы выбрали большую группу звезд в количестве N с координатами (li, bi)i=1N . В результате отождествления мы знаем их "двойников" из современного каталога. Обозначим координаты этих двойников, рассчитанные на момент t, через (Li(t), Bi(t))i=1N. Теперь предположим, что мы хотим проверить, какова была бы систематическая широтная ошибка в предположении, что дата составления каталога есть tA. Обозначим
LiA = Li(tA), BiA = Bi(tA) и введем широтную невязку Δ BiA = BiA - bi.
Наша цель -- минимизировать величину
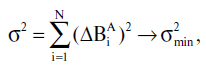
меняя систему координат, то есть, попросту, проводя новую координатную сетку, отличную от принятой в каталоге.
Изменение координатной сетки можно параметризовать двумя величинами, если мы рассматриваем задачу минимизации указанного выше выражения: γ и φ. Объясним их значение. Они показаны на приведенном ниже рис.5.1
. Здесь γ -- угол между реальной эклиптикой и эклиптикой каталога, а φ -- угол между прямой равноденствия и прямой пересечения реальной эклиптики с эклиптикой каталога.
Итак, минимизируя указанное выше выражение, можно найти значения γstat и φstat, параметризующие изменение системы координат и дающие исходный минимум. Их явный вид приведен ниже, в формулах (5.5.2) и (5.5.3).
Величина σmin является остаточной (после компенсации систематической ошибки) среднеквадратичной широтной ошибкой. Явный вид формулы для остаточной дисперсии σmin см. ниже после формулы (5.5.10). Он получается подстановкой γstat и φstat в качестве параметров в выражение для среднеквадратичного отклонения. Вывод этих формул приведен ниже.
Однако, мы не можем считать, что нашли систематическую ошибку (вернее, параметры γstat и φstat ее характеризующие) абсолютно точно. Дело в том, что индивидуальные ошибки измерения, носящие случайный характер, также влияют на значения γstat и φstat. Следовательно, мы можем лишь утверждать, что истинные значения систематической ошибки лежат где-то неподалеку от γstat и φstat.
Чтобы сделать утверждение более точным, введем понятие доверительного интервала. Зададимся некоторым уровнем доверия 1 − ε. Если, например, ε=0,1, то уровень доверия равен 0,9. Уровень доверия представляет собой вероятность, с которой мы гарантируем точность своих результатов. Доверительный же интервал представляет собой отрезок, накрывающий неизвестное нам истинное значение параметра с вероятностью не меньшей 1 − ε. Обозначим
Iγ(ε) = [γstat - xε, γstat + xε]
-- доверительный интервал для истинного значения параметра γ, и
Iφ(ε) = [φstat - yε, φstat + yε]
-- доверительный интервал для истинного значения параметра φ. Можно показать (см. ниже), что значения xε и yε можно вычислить по формулам
xε = qε, yε = qε, где qε представляет собой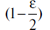 
-квантиль стандартного нормального распределения, который находится из таблиц.
Итак, если мы задаемся некоторым уровнем доверия 1 − ε, то с вероятностью не меньшей 1 − ε можно гарантировать принадлежность истинного значения γ интервалу Iγ(ε) и значения φ -- интервалу Iφ(ε).
0.3. ПО ЗНАЧЕНИЮ СИСТЕМАТИЧЕСКОЙ ОШИБКИ НЕЛЬЗЯ ДАТИРОВАТЬ КАТАЛОГ.
Дадим теперь несколько иную интерпретацию найденных значений γstat и φstat. Пользуясь значениями координат звезд (на самом деле, достаточно рассмотреть лишь широты), легко определяются полюса эклиптики PA (для изучаемого каталога) и P(t) (для расчетного каталога на момент t), рис.5b.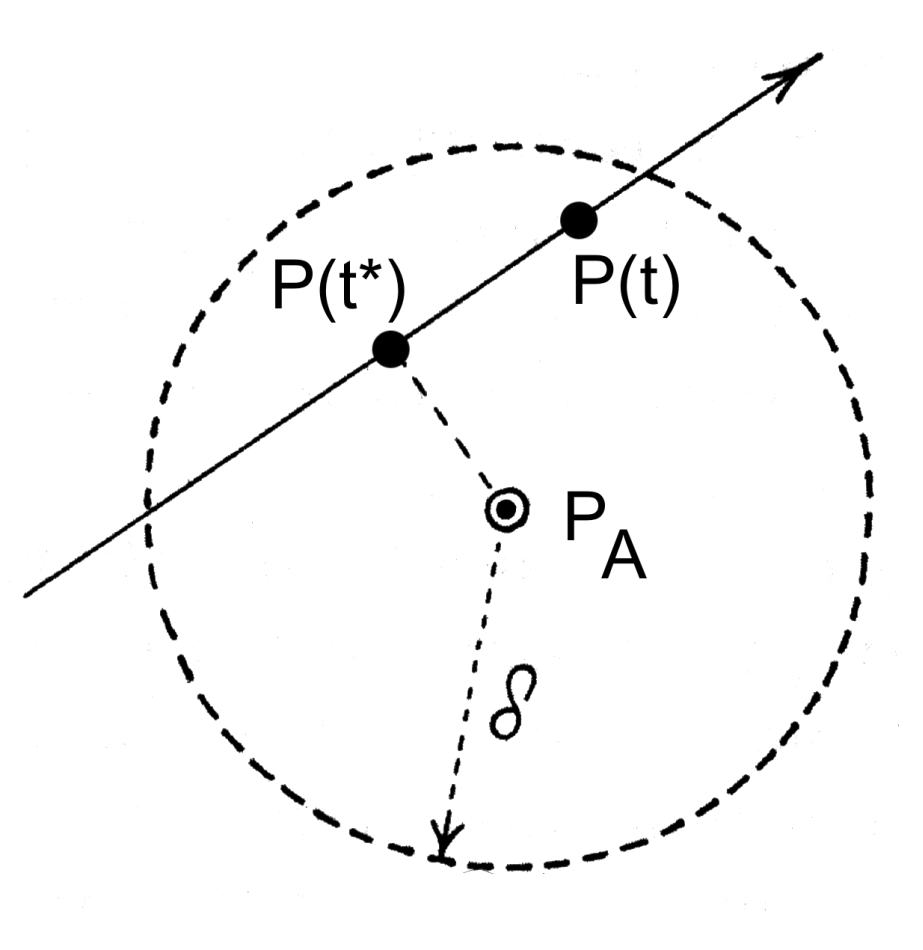
.
Очевидно, что дуговое расстояние между PA и P(t) равно в точности γstat и компенсация систематической ошибки есть не что иное, как совмещение этих полюсов. Теперь посмотрим, как эта картина меняется со временем. Поскольку движение P(t) происходит в пределах одного градуса, можно воспользоваться плоской картинкой и предположить равномерность движения P(t), см. рис.5b.
Скорость v этого равномерного движения нетрудно подсчитать, зная значения γstat в двух различных точках. Тогда легко найти момент t*, когда положение истинного полюса ближе всего отстоит от положения полюса каталога. На первый взгляд может показаться, что следует объявить этот момент искомой датировкой, вычисленной, кстати, обработкой значений координат большого количества звезд. Однако, как мы уже выяснили, логика эта неправильная и датировать каталог моментом t* нельзя. В самом деле, если возможная систематическая ошибка в определении эклиптики Птолемеем может достигать величины δ, то все моменты времени, отвечающие прохождению полюса P(t) через круг радиуса δ с центром в точке PA, должны рассматриваться как возможные кандидаты на время датировки. Но величину δ мы не знаем. Конечно, мы можем ее оценить, но лишь при условии, что нам известна датировка каталога. При другой предполагаемой датировке величина оценки будет другой. Таким образом, предполагаемая датировка уже заложена в оценке данной величины.
Поэтому, в зависимости от сделанной Птолемеем систематической ошибки, то есть ошибки в определении эклиптики, момент t* может оказаться либо более ранним, чем истинная дата составления каталога, либо более поздним. В первом случае каталог (вернее, та его часть, для которой ищется γstat) "удревняется" -- он, попросту, становится похож на каталог, составленный в году t*. Во втором случае, если t* -- момент более поздний, чем истинная дата составления, -- каталог омолаживается. Мы увидим далее, что обе эти возможности реализованы в Альмагесте. Однако, слова "удревняется" и "омолаживается" относятся к каталогу, в котором систематические ошибки не скомпенсированы. После их компенсации остается "рафинированный каталог", содержащий лишь случайные ошибки, среднеквадратичная величина которых оценивается значением σmin, но индивидуальные значения оценить невозможно.
Перейдем теперь к более подробной реализации изложенной выше общей идеи.
1. ОСНОВНЫЕ ОБОЗНАЧЕНИЯ.
Начиная с этой главы, мы считаем, что имеем дело с каталогом, все звезды которого имеют единственное отождествление со звездами из современного каталога. В соответствии с этим, будем идентифицировать звезды индексом i и обозначать через li, bi соответственно эклиптикальные долготу и широту i-й звезды в Альмагесте. Через Li(t), Bi(t) мы обозначим истинные долготу и широту i-й звезды в эпоху t. Напомним, что время t мы отсчитываем от 1900 года "назад" и измеряем в столетиях, то есть, например, t=3,15 соответствует году 1900-3,15 х 100=1585 году н.э., а t=22,0 отвечает году 1900-22 х 100=300 году до н.э.
Пусть tA -- неизвестное нам время составления каталога Альмагеста. Обозначим через LiA, BiA истинные долготу и широту i-й звезды в год составления каталога, то есть LiA=Li(tA), BiA=Bi(tA). Пусть Δ Bi(t)=Bi(t)-bi - разность между истинной широтой i-й звезды в момент времени t и ее широтой в Альмагесте. Назовем величину Δ Bi(t) широтной невязкой на момент времени t. Эта величина имеет смысл погрешности в определении широты i-й звезды Альмагеста при условии, что он составлен в эпоху t. Естественно, что Δ Bi(tA)=Δ BiA представляет собой истинную погрешность в определении широты.
Как уже отмечалось в главе 3, в случае с Альмагестом приходится анализировать лишь широтные ошибки. Причины этого подробно разъяснены выше.
