В.В.Калашников, Г.В.Носовский, А.Т.Фоменко
ЗВЕЗДЫ СВИДЕТЕЛЬСТВУЮТ.
Астрономический анализ хронологии.
Датировка Альмагеста Птолемея. Коперник, Тихо Браге и "античный" Гиппарх.

Том 3 , книга 1

Глава 5.
АНАЛИЗ СИСТЕМАТИЧЕСКИХ ОШИБОК ЗВЕЗДНОГО КАТАЛОГА.

5. СТАТИСТИЧЕСКИЕ СВОЙСТВА ОЦЕНОК γ_stat И φ_stat.

Сейчас мы подойдем к задаче оценки параметров γ и φ, задающих систематическую ошибку каталога, как к задаче статистической. Для этого поступим так. Пусть составитель каталога в момент времени t_A совершил систематическую ошибку, задаваемую параметрами γ_A и φ_A. Пусть, кроме того, широта каждой измеренной им звезды подвергалась, -- вследствие ошибки наблюдения, -- случайному возмущению ξ, имеющему нулевое среднее, то есть E}ξ_i=0. Предполагается, что случайные погрешности ξ_i, отвечающие различным звездам, независимы и имеют одно и то же распределение. Пусть σ²= E}ξ_i² -- дисперсия случайной величины ξ_i. Эта дисперсия нам, вообще говоря, неизвестна.

В этих предположениях широта i-той звезды в каталоге будет иметь вид

bi = Bi(tA) - γA sin(Li(tA) + φA) + ξi.

(5.5.1.)

Со статистической точки зрения мы имеем выборку, состоящую из N реализаций случайных величин {b_i}^N_i=1 вида (5.5.1). По этой выборке требуется определить статистические оценк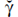и и 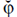параметров γ_A и φ_A, а также оценить величину σ, представляющую собой среднеквадратичную ошибку наблюдения. Мы сразу ограничим задачу и будем изучать оценки 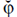= φ_stat и 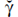= γ_stat, получаемые методом наименьших квадратов. Эти оценки имеют вид (5.3.6), (5.3.7). Основное внимание будет уделено оценке величины γ_A по причинам, объясненным в конце раздела 4.

Равенство (5.5.1) имеет вид, традиционный для регрессионного анализа. В самом деле, это равенство утверждает, что ошибка наблюдения Δ b_i = B_i(t_A) - b_i является случайной величиной со средним γ_A sin(L_i(t_A) + φ_A), зависящим от неизвестных параметров γ_A и φ_A, и дисперсией σ². Требуется оценить значения неизвестных параметров методом наименьших квадратов и установить статистические свойства полученных оценок. В такой постановке кривую Y(x) = γ_A sin(x + φ_A) обычно называют линией регрессии.

Определим величины φ и γ с помощью соотношений (5.3.6) и (5.3.7). Отклонения Δ b_i случайны по предположению. Поэтому и получаемые из соотношений (5.3.6) и (5.3.7) оценки φ_stat и γ_stat также являются случайными величинами. Изучим их статистические свойства и рассмотрим, как они связаны с истинными, но неизвестными нам, значениями φ_A и γ_A.

Подставим в приведенные выше формулы для s_b и c_b вместо Δ b_i разность γ_A sin(L_i(t_A) + φ_A) - ξ_i и используем эту подстановку в формулах (5.3.6), (5.3.7). Получим следующие выражения для величин φ_stat и γ_stat.

Если ошибки наблюдения ξ_i нормально распределены, то и величина γ_stat является нормально распределенной, и первые два момента (5.5.5) и (5.5.6) полностью определяют ее распределение. Этот факт даст нам возможность построить доверительный интервал для значения γ_A.

Анализ оценки φ_stat несколько более сложен. Воспользуемся следующим равенством, получаемым из (5.5.4):

и тем фактом, что при больших N второе слагаемое в знаменателе правой части (5.5.7) -- величина малая. В самом деле, эта величина -- случайная с нулевым средним и дисперсией

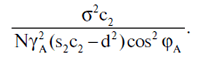
Если ξ_i нормально распределены, то и рассматриваемая величина также нормально распределена. Из этого факта для каталога Альмагеста следует, что уже для N=30 вероятность p_N того, что знаменатель правой части (5.5.7) будет отрицательным, не превосходит 5 x10^-3. С ростом N данная вероятность быстро убывает: p₅₀ ≤ 2,5 x 10^-4, p₈₀ ≤ 4 x 10^-6, p₁₀₀ ≤ 3 x 10^-7, p₂₀₀ ≤ 8 x 10^-13, p₃₀₀≤ 2,5 x 10^-18.

Из формулы (5.5.7) следует, что, вообще говоря, Etanφ_stat ≠ tanφ_A. Однако из этой формулы легко получить функцию распределения F(x) случайной величины tanφ_stat - tanφ_A, необходимую при нахождении доверительного интервала для φ_A. В самом деле, если пренебречь тем маловероятным случаем, что знаменатель в (5.5.7) становится отрицательным, то из этой формулы получается выражение для F(x):

F(x) =P(tanφ_stat - tanφ_A < x) = P(η_x < x), где случайная величина η_x имеет вид

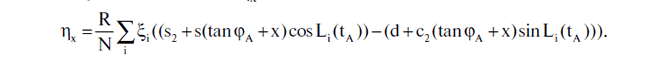
Следовательно, если величины ξ_i нормально распределены с дисперсией σ², то и величина η_x имеет гауссовское распределение со средним, равным нулю, и дисперсией

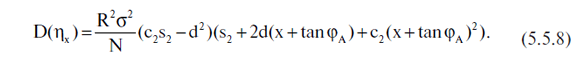
Следовательно,

где

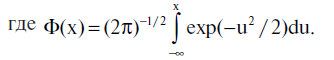
Найденные выше значения γ_stat и φ_stat являются, как говорят, точечными оценками неизвестных параметров γ_A и φ_A. Поскольку найдены функции распределения этих оценок, то можно исследовать вопрос об их возможной погрешности. Дадим ответ на этот вопрос в стандартных терминах доверительных интервалов, основываясь на формулах (5.5.5), (5.5.6), (5.5.8), (5.5.9).

В математической статистике задача нахождения доверительного интервала порождена следующей ситуацией, которую поясним на примере оценки величины γ_A. Эта величина является вполне определенной, детерминированной ошибкой, сделанной составителем каталога. В результате статистической оценки γ_A, -- в нашем случае по методу наименьших квадратов -- получается случайная величина γ_stat. Возникает вопрос, какие границы можно указать для неизвестной нам величины γ_A, если мы определили γ_stat?

Чтобы границы эти не оказались тривиальными, необходимо задать допустимую вероятность ошибки, то есть, вероятность указать такие границы, в которых истинное значение γ_A не лежит. Обозначим допустимую вероятность ошибки через ε. Тогда уровень доверия будет равен равен 1 - ε. Случайная величина γ_stat распределена по нормальному закону с параметрами, задаваемыми формулами (5.5.5) и (5.5.6). Поэтому при x > 0 имеем

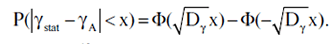
Определим величину ε/2-квантили нормального распределения x_ε из уравнения

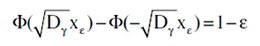
или, что то же, из уравнения

Тогда интервал

Iγ(ε) = (γstat - xε, γstat + xε)

(5.5.10)

представляет собой доверительный интервал для γ_A с уровнем доверия 1 - ε. Это следует из того, что P(|γ_stat - γ_A| ≥ x_ε) = ε.

При определении величины x_ε мы, в частности, использовали значение {\bf D}_γ, которое зависит от неизвестных нам параметров σ² и φ_A. Как это обычно делается в математической статистике, вместо σ² подставим в формулу для D_γ сходящуюся к ней остаточную дисперсию

определяемую формулой (5.3.3), а вместо φ_A -- величину φ_stat. Момент t_A составления каталога нам также неизвестен, поэтому все перечисленные выше вычисления необходимо проделать для всех моментов времени t с тем, чтобы оценить систематическую ошибку γ_stat(t), φ_stat(t) при условии, что каталог был составлен в произвольную фиксированную эпоху t.

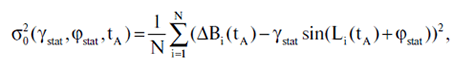
Аналогичным образом можно найти доверительный интервал для φ_A с уровнем доверия 1 - ε. Этот интервал I_φ(ε) будет таким:

где y_ε -- решение уравнения F(y_ε) - F(-y_ε) = 1 - ε, в котором функция распределения F задана равенством (5.5.9), то есть ε/2-квантиль соответствующего нормального распределения.

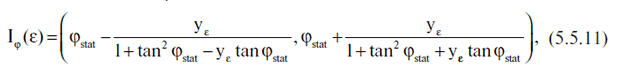
Замечание. Полученные выше оценки истинных значений ошибок γ и φ в каталоге, как функций предполагаемой датировки, важны не только для того, чтобы их скомпенсировать, но и для косвенной проверки правильности предлагаемого подхода. Например, если бы в качестве γ_stat получилась величина, в несколько раз превышающая точность каталога, это указывало бы на какие-то неучтенные нами существенные эффекты.

Однако если речь идет лишь о датировке, то само значение γ_stat в соответствующей процедуре не участвует. Нам необходимо лишь знание длины соответствующего доверительного интервала. Поэтому возможно существенное упрощение вычислений, состоящее в следующем. Вычисляются γ_stat и φ_stat, относящиеся к любому фиксированному моменту времени t₀. Например, к 1900 году, для чего не требуется использования уравнений Ньюкомба. Тогда вместо кривых γ_stat(t) и φ_stat(t) мы получим постоянные значения, соответствующие ошибкам наблюдений, но только не в координатах эпохи наблюдений, а в координатах эпохи 1900 года. Затем вокруг этих постоянных значений откладываются доверительные интервалы, ширина которых от t не зависит. В результате статистической процедуры датировки, описываемой ниже, будет получен тот же интервал возможных датировок каталога, что и при оценивании ошибок γ и φ относительно координат на эпоху предполагаемой датировки t. Единственная информация, которая при этом будет потеряна, -- это оценки истинных значений величин γ_stat и φ_stat.

 

 

6. ВЫВОДЫ

ВЫВОД 1. Групповая ошибка звездной конфигурации сводится к перемещению этой конфигурации как единого целого по небесной сфере. Данное перемещение, при учете лишь широтных невязок, можно параметризовать двумя параметрами, а именно, γ и φ, либо γ и β.

ВЫВОД 2. Существующие в каталоге широтные невязки могут быть уменьшены за счет компенсации групповых ошибок.

ВЫВОД 3. Если в большой части каталога групповые ошибки совпадают, то эта общая ошибка называется систематической и может быть обнаружена статистическими методами.

При условии, что каталог составлен в эпоху t, значения параметров φ(t) и γ(t) оцениваются методом наименьших квадратов. Соответствующие оценки φ_stat(t) и γ_stat(t) имеют вид (5.3.6) и (5.3.7) соответственно.

ВЫВОД 4. Знания значений γ_stat(t₁) и γ_stat(t₂) для двух различных моментов времени достаточно для восстановления функций γ_stat(t) и φ_stat(t).

ВЫВОД 5. В предположении нормального распределения случайных ошибок измерения найдены доверительные интервалы I_φ(ε) и I_γ(ε) для истинных значений параметров φ(t) и γ(t). См. формулы (5.5.11) и (5.5.10) соответственно.

В заключение, на рис.5.8, приведем страницу из Альмагеста издания 1551 года.