В.В.Калашников, Г.В.Носовский, А.Т.Фоменко
ЗВЕЗДЫ СВИДЕТЕЛЬСТВУЮТ.
Астрономический анализ хронологии.
Датировка Альмагеста Птолемея. Коперник, Тихо Браге и "античный" Гиппарх.

Том 3 , книга 1

Глава 7.
ДАТИРОВКА ЗВЕЗДНОГО КАТАЛОГА АЛЬМАГЕСТА.
СТАТИСТИЧЕСКИЙ И ГЕОМЕТРИЧЕСКИЙ МЕТОДЫ.

8. УСТОЙЧИВОСТЬ ГЕОМЕТРИЧЕСКОГО МЕТОДА ДАТИРОВКИ КАТАЛОГА АЛЬМАГЕСТА. ВЛИЯНИЕ ВОЗМОЖНЫХ ПОГРЕШНОСТЕЙ АСТРОНОМИЧЕСКОГО ПРИБОРА НА РЕЗУЛЬТАТ ДАТИРОВАНИЯ.

8.1. ПОГРЕШНОСТИ В ИЗГОТОВЛЕНИИ АСТРОНОМИЧЕСКИХ ПРИБОРОВ МОГЛИ ВЛИЯТЬ НА ТОЧНОСТЬ ИЗМЕРЕНИЙ.

В геометрическом способе датирования отсутствует доверительная вероятность ε. Однако необходимо проверить его устойчивость по отношению к заявленной точности каталога и к составу информативного ядра. Выводы здесь во многом аналогичны выводам раздела 6. Так, повышение уровня точности с 10' до 15' приводит, как и в разделе 6, к сдвигу нижней границы интервала датировки вниз до 250 года н.э. Для уменьшенного информативного ядра из тех шести звезд прежнего ядра, которые находятся либо в области Zod A, либо в ее окрестности, интервал датировки увеличился всего лишь примерно на 100 лет, а именно, он расширился от 500 года н.э. до 1300 года н.э. Удаление же из информативного ядра каталога быстро движущегося Арктура приводит к расширению интервала датировки от 200 года н.э. до 1600 года н.э.

Таким образом, ни в каком случае интервал датировки каталога Альмагеста, полученный геометрической процедурой, не накрывает скалигеровскую эпоху Птолемея. Не говоря уж о "скалигеровском" Гиппархе.

Кроме того, мы докажем устойчивость геометрической процедуры датировки к возможным погрешностям астрономического прибора наблюдателя.

Геометрический метод датировки основан на учете ошибки наблюдателя в определении полюса эклиптики. Рассматриваются все возможные вращения сферы, или, другими словами, -- ортогональные повороты координатной сетки в пространстве. Если интересоваться только широтами, то вращение сферы можно задавать лишь вектором смещения полюса, поскольку оставшаяся компонента вращения не меняет широт.

Пусть вектор смещения полюса имеет координаты (γ, φ). Если удастся найти такое вращение сферы, которое опускает максимальную широтную невязку, -- например, по информативному ядру каталога, или по зодиакальным звездам каталога и т.п., -- ниже уровня Δ, то мы сможем датировать каталог. Напомним, что для каталога Альмагеста Δ=10'.

Во всех рассмотренных выше случаях, ортогональных вращений звездной сферы было достаточно, чтобы опустить максимальную широтную невязку ниже заявленной точности каталога Δ. И тем самым датировать каталог, а заодно -- подтвердить точность Δ, заявленную Птолемеем. Однако, до сих пор мы не учитывали, что Птолемей мог пользоваться несовершенным астрономическим прибором. Например, астролябией, включающей в себя металлические ко'льца, слегка отклоняющиеся от идеального кольца, окружности. Кольцо могло быть слегка сжато с одного края и растянуто с другого. Кроме того, некоторые в идеале перпендикулярные плоскости этого прибора, могли оказаться по тем или иным причинам не совсем перпендикулярными. Мог возникнуть перекос углов. В результате, по разным осям мог появиться слегка разный масштаб.

Другими словами, прибор и, следовательно, определяемая им координатная сетка в трехмерном пространстве, могли подвергаться некоторой деформации. Это могло сказаться на результате измерений и исказить результат. Возникает естественный вопрос. Как влияют малые деформации прибора, или, другими словами, -- соответствующей ему трехмерной координатной сетки, -- на результат измерений? Насколько должны быть значительны искажения инструмента, чтобы они стали заметно сказываться на результатах наблюдателя? Ниже мы даем полный ответ на эти вопросы.

 

8.2. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ.

Сформулируем задачу в точных математических терминах. Рассмотрим трехмерное евклидово пространство, в центре которого помещена сфера, отнесенная к трем взаимно ортогональным координатным осям. Эти оси определяют попарно ортогональные координатные плоскости. Измерение эклиптикальных координат звезд заключается в том, что звезда проектируется из начала координат на поверхность сферы в точку A, рис.7.32. Полученной точке A на сфере сопоставляются ее координаты, -- например, сферические. Эти координаты наблюдатель заносит в свой каталог.

Будем считать для простоты, что ось z направлена на полюс эклиптики P, а плоскость xy пересекает сферу по эклиптике. Как мы уже подробно разъяснили, более надежно измеряемыми координатами являются широты звезд. Поэтому в первую очередь мы интересуемся именно широтой звезды A. Широта измеряется вдоль меридиана, соединяющего полюс эклиптики P со звездой A. Нулевой широте отвечает сама эклиптика, то есть нулевая параллель. На рис.7.32 эклиптикальная широта звезды A измеряется длиной дуги AB.

В описанном выше занесении координат звезды в каталог заложено предположение, что прибор наблюдателя порождает идеальную сферическую систему координат в трехмерном окружающем пространстве. Однако реальный прибор может быть слегка деформирован. Пренебрегая эффектами второго порядка, без ограничения общности можно считать, что деформация прибора вызывает некоторое линейное преобразование евклидовой системы координат в пространстве. Естественно считать это линейное преобразование близким к тождественному, так как слишком сильное искажение прибора будет замечено наблюдателем, претендующим, как мы видели, на точность 10'. Даже если деформация системы координат и содержит малые нелинейные возмущения, фактически мы рассматриваем первое приближение, то есть линейную аппроксимацию, описывающую искажение прибора.

Линейное преобразование трехмерного пространства, оставляющее на месте начало координат, задается матрицей

Это преобразование, действуя на исходную евклидову систему координат, искажает ее. Из элементарной теории квадратичных форм хорошо известно, что невырожденное линейное преобразование, близкое к тождественному, деформирует сферу в некоторый эллипсоид, рис.7.33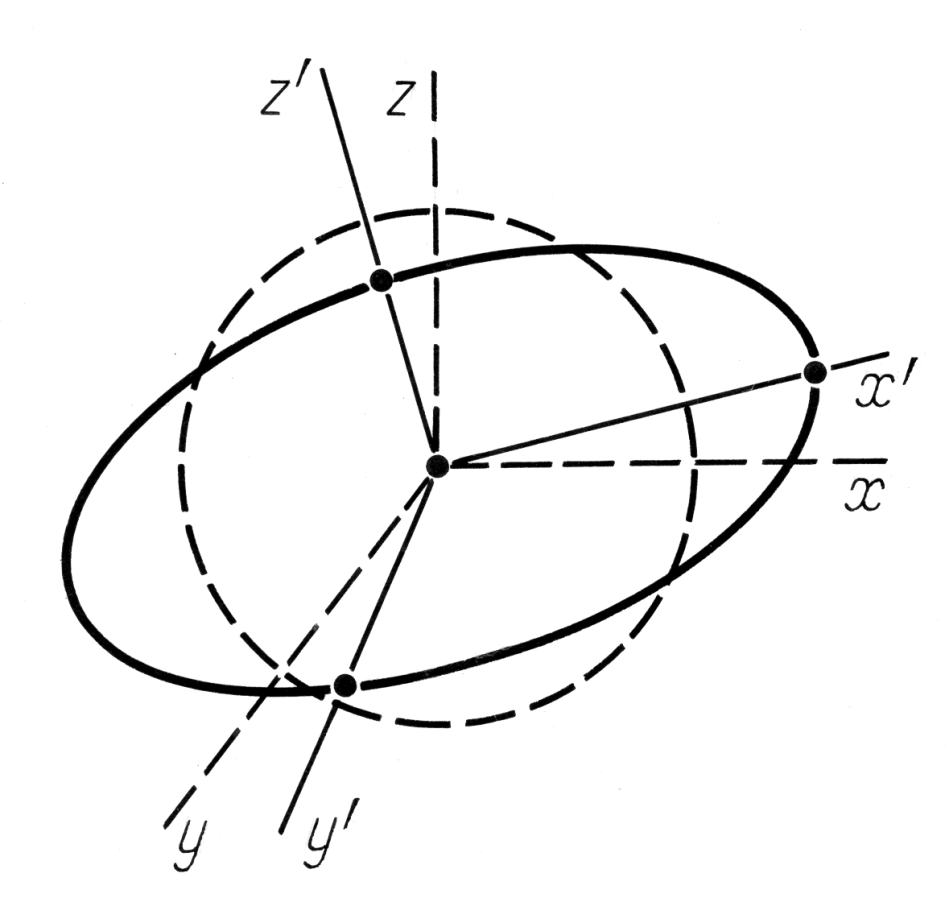. Таким образом, хотя исходные взаимно ортогональные координатные прямые слегка смещаются, и вообще говоря, перестают быть ортогональными, всегда найдутся новые три взаимно ортогональные прямые, направленные по осям эллипсоида. Эти три новые прямые обозначены на рис.7.33 буквами x', y', z'.

Таким образом, для наших целей можно считать, что линейное преобразование деформирует сферу следующим образом. Сначала происходит некоторый поворот (ортогональное преобразование), переводящий оси x, y, z в новые взаимно ортогональные оси x', y', z'. Затем происходит растяжение по трем взаимно ортогональным направлениям с некоторыми коэффициентами λ₁, λ₂, λ₃. Это последнее преобразование однозначно задается диагональной матрицей

Коэффициенты растяжения λ₁, λ₂, λ₃ -- это некоторые вещественные числа. Из самого смысла задачи следует, что они отличны от нуля.

 

8.3. ИСКАЖЕНИЕ СФЕРЫ В ЭЛЛИПСОИД.

Деформации координатной сетки, вызванные ортогональными поворотами, изучены выше, поэтому теперь можно сосредоточиться на втором преобразовании, а именно на преобразовании подобия, задаваемом диагональной матрицей R.

Итак, без ограничения общности можно считать, что деформация астрономического прибора, порождающая линейное преобразование трехмерной евклидовой координатной сетки в пространстве, задается преобразованием подобия R с коэффициентами растяжения λ₁, λ₂, λ₃, рис.7.34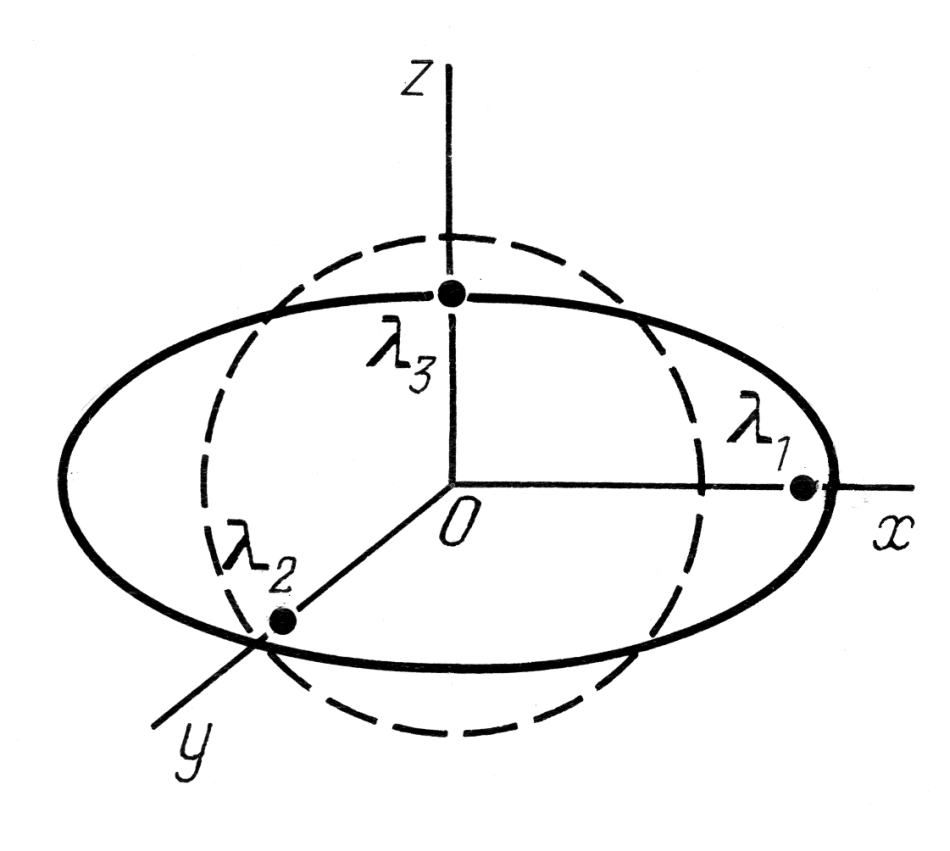. Отметим, что числа λ_i могут быть б'ольшими единицы, равными единице или меньшими единицы независимо друг от друга. Поэтому, говоря о коэффициентах растяжения, мы в действительности имеем в виду не только фактическое растяжение (увеличение линейного размера вдоль оси), но и возможное сжатие, то есть уменьшение линейного размера. Если при некотором i выполнено неравенство λ_i > 1, то мы имеем растяжение. Если же λ_i < 1, то вдоль данной оси происходит сжатие.

Числа λ₁, λ₂, λ₃ можно рассматривать как величины полуосей эллипсоида. На рис.7.34 эти полуоси изображаются отрезками Oλ₁, Oλ₂, Oλ₃.

 

8.4. НЕТОЧНОСТИ ИЗМЕРЕНИЙ В "ЭЛЛИПСОИДАЛЬНОЙ СИСТЕМЕ КООРДИНАТ".

Обсудим подробнее измерение координат звезды в описанной выше искаженной системе координат, которую мы назовем эллипсоидальной. На рис.7.35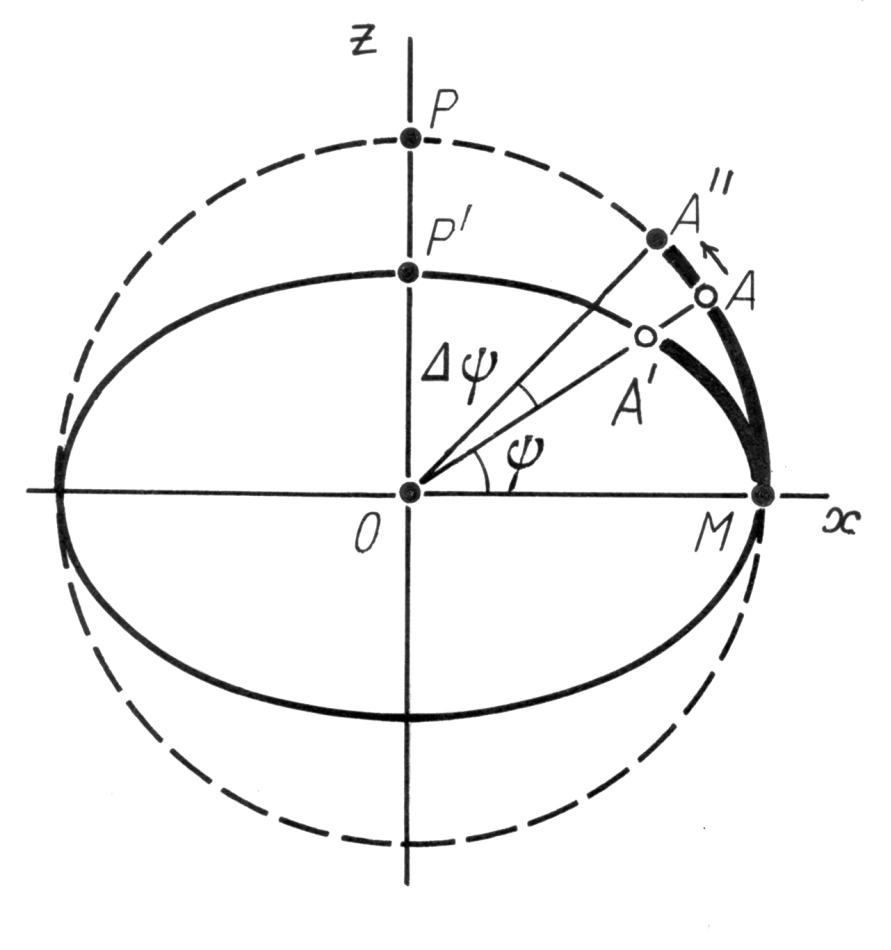 плоскость рисунка проходит через центр O, звезду A и полюс эклиптики P. Эта плоскость рассекает эллипсоид, порождаемый прибором, по эллипсу, показанному на рис.7.35 сплошной линией. Соответствующая окружность, которая порождалась бы идеальным прибором, показана пунктиром. Сейчас нас интересуют лишь широты, поэтому напомним, что широты обычно отсчитываются от эклиптики, то есть от точки M на рис.7.35. Наблюдатель разделил дугу MP' на 90 равных частей и тем самым градуировал кольцо (эллипс), отметив на нем градусные деления. Так как на самом деле он градуировал не окружность, а эллипс, то равномерные градусные деления на эллипсе слегка искажают углы. Следовательно, возникающая градуировка углов неравномерна. Мы считаем здесь, что наблюдатель этого не заметил, иначе бы он исправил прибор.

Наблюдая реальную звезду A, наблюдатель отметил ее положение A' на своем "эллипсоидальном приборе". Он получил, по его мнению, реальную широту звезды. Занося это число в свой каталог, который, естественно, предполагает в качестве системы координат идеальную сферическую систему, наблюдатель получил некоторую точку A''. Тем самым он сместил положение звезды, слегка поднял ее по отношению к истинному, если, например, λ₁ > λ₃, как показано на рис.7.35.

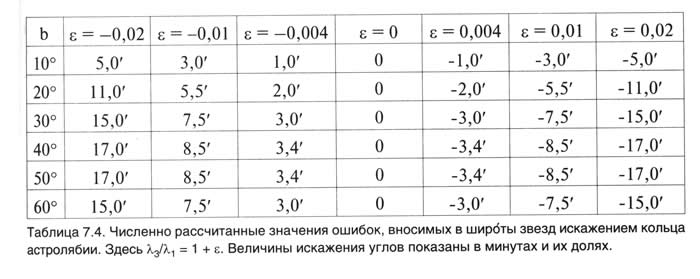
Возникающее преобразование окружности, а именно A -----> A'', конечно, нелинейно. Его можно продолжить до преобразования всей плоскости и всего трехмерного пространства. При этом начало координат остается на месте. Однако, поскольку мы считаем искажения прибора все-таки незначительными, то, как уже было сказано выше, можно ограничиться рассмотрением линейного приближения. То есть, заменить, -- не делая при этом большой ошибки, -- описанное нелинейное преобразование его главной линейной частью. Такой главной частью является растяжение по трем взаимно ортогональным осям с коэффициентами λ₁, λ₂ и λ₃. Таким образом, мы снова возвращаемся к уже описанной выше математической постановке задачи. См. пункты 8.2 и 8.3. Точные значения искажений, вносимых указанным преобразованием в широты звезд, были нами рассчитаны на компьютере. Результаты расчетов приведены в табл.7.4.

 

8.5. ОЦЕНКА ИСКАЖЕНИЙ УГЛОВ, ИЗМЕРЯЕМЫХ "СЛЕГКА ЭЛЛИПСОИДАЛЬНЫМ ПРИБОРОМ".

Итак, пусть задано линейное преобразование трехмерного пространства, определяемое тремя числами λ₁, λ₂ и λ₃, то есть матрицей

Нам необходимо оценить возникающее при этом искажение углов. Пусть ψ -- истинная широта реальной звезды. Измерение на эллипсоидальном приборе превратит ее в некоторое другое число ψ'. Разность Δ ψ = ψ - ψ' дает величину возникшего искажения. С геометрической точки зрения искажение задается углом Δ ψ между направлением на реальную звезду и тем направлением на нее, которое вычисляется на искаженном приборе.

Оказывается, можно не рассматривать все трехмерное пространство, а ограничиться лишь плоским случаем. В самом деле, на рис.7.36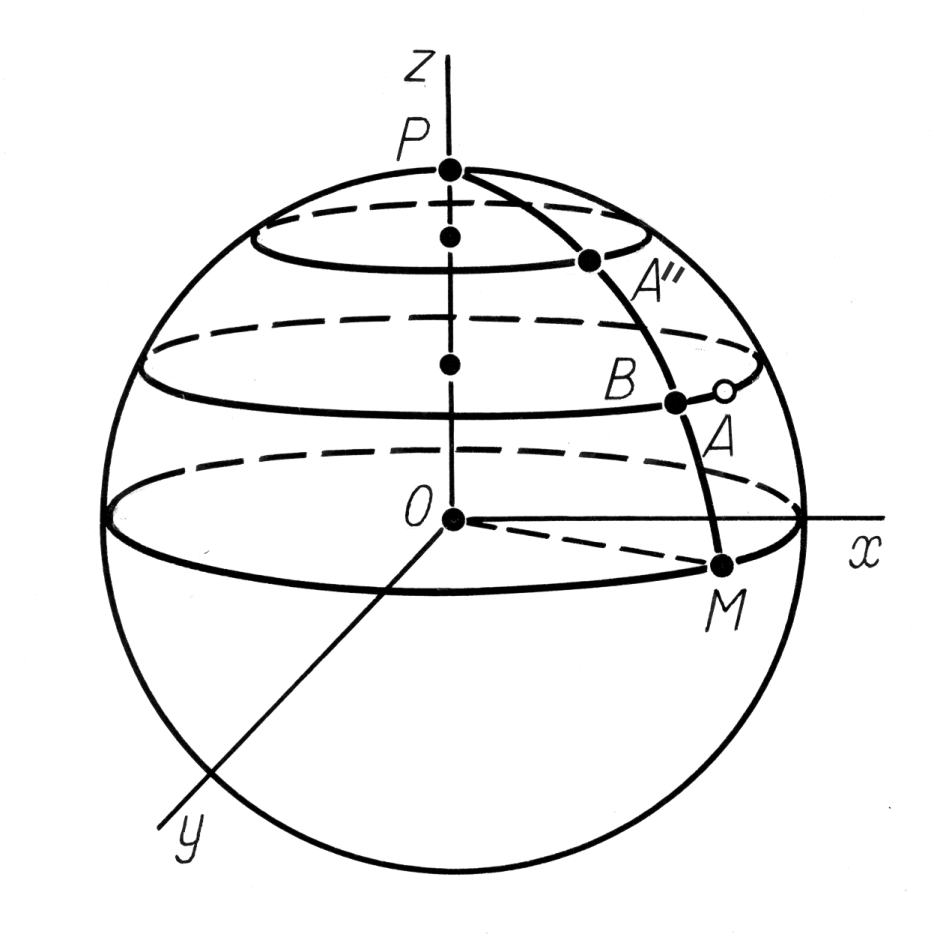 видно, что под действием линейного преобразования R звезда A перейдет в новое положение A''. При этом параллель звезды A перейдет в параллель звезды A''. Дело в том, что плоскость, ортогональная оси OP и определявшая параллель звезды A, перейдет в плоскость, также ортогональную оси OP. Так как нас интересуют лишь широты, то вместо точки A достаточно рассмотреть точку B, лежащую на меридиане звезды A'', рис.7.36.

Под действием преобразования R плоскость, проходящая через ось OP и меридиан звезды A, поворачивается вокруг оси OP. При этом в повернутой плоскости возникает линейное преобразование подобия. Следовательно, трехмерная задача сводится к двумерной. Поэтому в дальнейшем мы рассмотрим эллипс в двумерной плоскости, рис.7.37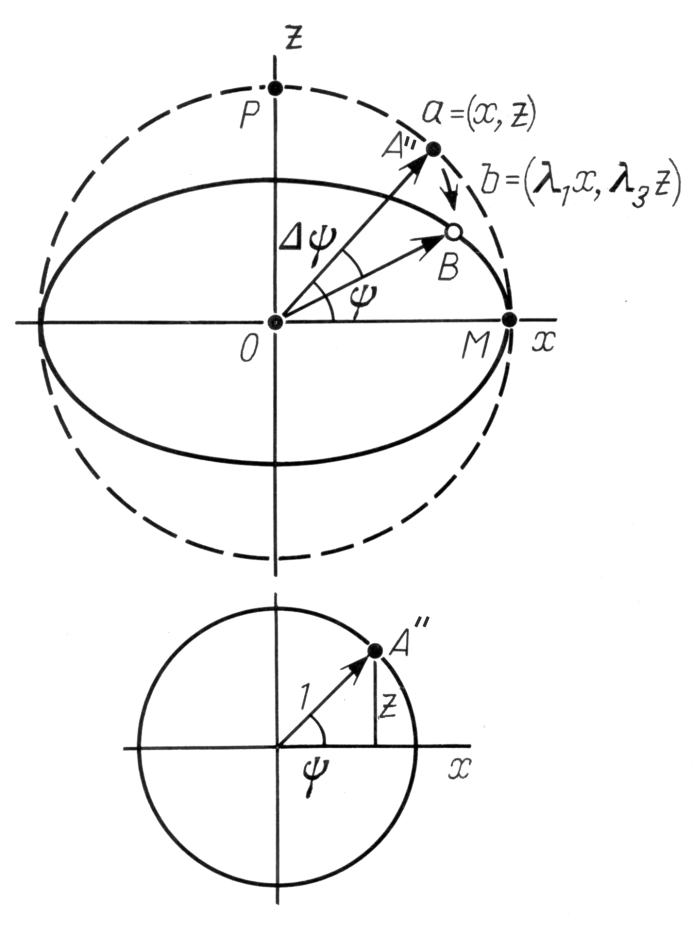. Отвлекаясь от предыдущих обозначений, введем на плоскости декартовы координаты (x,z) и рассмотрим линейное преобразование

определяемое растяжениями λ₁ и λ₃ вдоль осей x и z соответственно.

Положение звезды A'' задается на единичной окружности радиус-вектором a=(x,z), а точка B -- радиус-вектором b = (λ₁x, λ₃z). Наша цель -- вычислить угол Δ ψ как функцию от широты ψ и коэффициентов растяжения (сжатия) λ₁ и λ₃.

 

8.6. ОЦЕНКА ВОЗМОЖНЫХ ИСКАЖЕНИЙ И УСТОЙЧИВОСТЬ ПОЛУЧЕННОЙ НАМИ ДАТИРОВКИ.

Из элементарных теорем аналитической геометрии следует, что cos Δ ψ равен скалярному произведению (a,b) векторов a и b, деленному на длину вектора b. При этом мы, естественно, считаем радиус окружности OM равным 1. Этого всегда можно добиться выбором соответствующего масштаба. Итак,

Теперь найдем конкретные численные оценки для ε. Напомним, что λ₃/λ₁ = 1 + ε, то есть величина ε показывает степень искажения системы координат. Участвующие в наших формулах величины удобно измерять в радианах. Имеем: 1^o = π/180; 1'=1^o/60 = 3,14/(60x180) ≈ 4,35 x 10^-4, то есть 1' ≈ 0,00044.

Следовательно, при разумно допустимых значениях ε, -- то есть при искажениях прибора, которые незаметны невооруженным глазом, -- широты звезд, близких к эклиптике или к полюсу, искажаются очень незначительно. Дело в том, что sin2ψ стремится в этих случаях к нулю. Это говорит о том, что разумно допустимые искажения прибора не могут существенно повлиять на результат измерений звезд с малой и с большой широтами, то есть, с широтами, близкими к 0 градусов или к 90 градусам. Наибольшие искажения широт могут произойти для звезд, удаленных от эклиптики и от полюса эклиптики.

Дадим количественные оценки на конкретном материале звездных каталогов. Рассмотрим, например, Альмагест. Как видно из рис.7.27, график максимальной широтной невязки информативного ядра Альмагеста достаточно быстро нарастает справа и слева от интервала 600--1300 годы н.э. Возникает вопрос. Можно ли, допустив искажения прибора, "подавить", то есть уменьшить, эту широтную невязку, например, около начала нашей эры, то есть, в ту эпоху, когда, согласно скалигеровской версии хронологии, создан Альмагест?

Другими словами, можно ли обосновать "скалигеровскую" гипотезу, состоящую в том, что звездный каталог Альмагеста создан все же около начала нашей эры. Однако наблюдатель, дескать, пользовался слегка искаженным прибором. В результате чего внес некоторую ошибку в широты звезд. Можно ли, учитывая эту ошибку, датировать каталог эпохой, близкой к началу нашей эры?

Покажем, что на самом деле этого сделать нельзя. Допустим, что на измерения повлияли искажения астрономического прибора. Попытаемся, учитывая их, уменьшить широтную невязку по информативному ядру Альмагеста в предположении, что звезды наблюдались около начала н.э. Но, как мы подсчитали выше, эта невязка достаточно велика. Она составляет не менее 35' около 0-го года н.э. Можно ли подавить ее, подобрав подходящее ε?

Как было показано, подавить широтную невязку за счет звезд с малыми и большими широтами практически невозможно. Однако можно попытаться сделать это, используя звезды с широтами, близкими к 30^o--40^o. В информативном ядре Альмагеста имеется Арктур, широта которого составляет 31 градус. Более того, ввиду значительной собственной скорости, Арктур дает основной вклад в формирование максимальной широтной невязки информативного ядра около начала нашей эры. Как видно из рис.7.31, график индивидуальной широтной невязки Арктура таков, что около начала нашей эры эта невязка как раз и достигает примерно 35'. Итак, можно ли существенно уменьшить невязку по Арктуру вблизи скалигеровской датировки Альмагеста, допустив, что наблюдатель пользовался искаженным прибором?

Вычислим значение ε. Как уже отмечалось, точность Δ каталога Альмагеста, заявленная его составителем, равна 10'. Следовательно, чтобы подавить широтную невязку Арктура, уменьшив ее с 35' до 10', следует уменьшить широту примерно на 25'. Таким образом, следует подобрать такое ε, чтобы Δ ψ равнялось 25'. В радианах Δ ψ = 0,01. Из формулы для ε сразу получаем, что

Итак, ε должно быть равным примерно 0,023. Только такими искажениями прибора можно пытаться объяснить широтную ошибку Арктура при наблюдениях около начала нашей эры. Но это значение ε слишком велико! Например, если радиус астролябии составляет 50 см, то прибор должен быть искажен так, чтобы одна из полуосей стала равной 51 см. Другими словами, ошибка должна составлять около 1 см! Допустить такую огромную ошибку для астрономического прибора вряд ли возможно. Иначе придется предположить, что во времена Птолемея колеса телег изготовлялись с большей точностью, чем кольца астролябии.

 

8.7. ТАБЛИЦА ЧИСЛЕННЫХ ЗНАЧЕНИЙ ВОЗМОЖНЫХ "ЭЛЛИПСОИДАЛЬНЫХ ИСКАЖЕНИЙ".

Выше мы привели таблицу значений искажений, возникающих при измерении широт звезд с помощью некоторого прибора, например, астролябии, с эллипсоидально деформированным широтным кольцом. Отметим, что величина искажения широты звезды A зависит от значения истинной широты звезды A и от величины λ = R₃/R₁. Здесь R₁ и R₃ - это полуоси эллипсоидального широтного кольца прибора. Положим, как и выше, λ = 1 + ε. Тогда значение ε=0 соответствует идеальному кольцу, то есть когда эллипс превращается в окружность. Следовательно, в этом случае искажения будут равны нулю на всех широтах. Как видно из табл.7.4, максимальные по абсолютной величине искажения появляются на широте 45 градусов. Это нетрудно показать также и теоретически. В табл.7.4 приведены значения разности b'-b, где b -- точное значение широты звезды, а b' -- значение широты, измеренное по отметкам на эллипсоидальном кольце с параметром λ=1 + ε. Величины b и ε являются входами таблицы. Значения искажений b'-b были рассчитаны нами численно, с помощью компьютера.

Таблица 7.4.

Из табл.7.4 видно, какую погрешность мы допускаем, заменяя рассмотренное выше нелинейное преобразование координатной сетки его главной линейной частью. Учет этой погрешности не меняет наших выводов относительно невозможности допустить такие искажения прибора Птолемея, которые привели бы к расширению интервала датировок до скалигеровской эпохи Альмагеста: I-II века н.э.

 

8.8. ВЫВОДЫ.

1) Теоретически возможны искажения астрономического прибора, приводящие к тому, что порождаемая им система координат в пространстве подвергается некоторому линейному преобразованию.

2) Можно теоретически вычислить зависимость между коэффициентом ε искажения прибора и возникающей при этом ошибкой в определении широт звезд.

3) Опираясь на материал конкретных каталогов, например, Альмагеста, можно найти численные значения для ε и Δ ψ.

4) Никакими разумными искажениями астрономического прибора нельзя объяснить слишком большую широтную ошибку, найденную в каталоге Альмагеста при условии, что наблюдения проводились около начала н.э.

5) Полученные нами выше результаты, -- включая датировку каталога Альмагеста 600--1300 годами н.э., -- устойчивы к допущению разумно малых искажений наблюдательного прибора. Другими словами, введя гипотезу о возможном искажении прибора, все равно нельзя датировать каталог Альмагеста эпохами около начала нашей эры.