ПРИЛОЖЕНИЕ 4.
ИСТОРИЯ МАТЕМАТИКИ В СКАЛИГЕРОВСКОЙ ВЕРСИИ ВЫГЛЯДИТ ОЧЕНЬ СТРАННО.
Скалигеровская история вынуждает нас относить математические труды «античных» авторов в глубокую древность. Это приводит к многочисленным и ярким странностям и даже противоречиям в истории математики. Например, возникают парадоксальные ситуации, когда достаточно сложные математические задачи решаются якобы на основе примитивных, чуть ли не «пещерных» обозначений и понятий. Такой разрыв между уровнем обозначений и сложностью решаемых задач иногда доходит до абсурда. Как, например, в успешно решавшейся «древне»-вавилонской задаче о расчете и предсказании солнечных затмений при помощи якобы лишь двух цифр-клинышков.
Тем читателям, которые все же захотят настаивать на верности скалигеровской картины, предлагаем решить следующие три математические задачи, опираясь исключительно на «античные» обозначения, которые мы сейчас приведем.
ПЕРВАЯ ЗАДАЧА – «ДРЕВНЕ»-ВАВИЛОНСКАЯ.
Согласно скалигеровской истории, нижеприведенные математические задачи успешно решались за две тысячи лет до нашей эры в «древнем» Вавилоне [56], с.100. Причем с помощью всего лишь ДВУХ цифр-клинышков. А именно, вертикальный клин обозначал «единицу», а горизонтальный клин – «десять». Остальные числа от 1 до 59 записывались сочетанием вертикальных и горизонтальных клинышков в соответствующем количестве. Например, число 23 записывалось группой из двух горизонтальных и трех вертикальных клиньев. При этом число 60 СНОВА записывалось при помощи одного вертикального клина [56], с.98. Таким образом, в этой системе было всего лишь две цифры и основанием системы служило число 60. Кроме того, не ставилось никакого знака, соответствующего современной запятой, отделяющего дробную часть от целой. Это, конечно, вносило неоднозначность в запись чисел. Например, запись:
<
как сообщают нам историки математики, «могла означать число 83. Мы пишем “могла означать”, так как запись эта могла быть прочитана многими способами: она могла означать 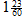 , или 602+23 и вообще 60k+23
, или 602+23 и вообще 60k+23![]() 60m, где m<k” [56], с.98. Историки математики правильно отмечают далее: «такая неоднозначность записи объяснялась тем, что у вавилонян не было нуля» [56], с.98. “Правда, в эпоху Селевкидов появился специальный разделительный знак (прообраз нашего нуля), который ставился, если в числе был пропущен какой-нибудь шестидесятиричный разряд. Однако в конце числа этот знак никогда не ставился” [56], с.98.
60m, где m<k” [56], с.98. Историки математики правильно отмечают далее: «такая неоднозначность записи объяснялась тем, что у вавилонян не было нуля» [56], с.98. “Правда, в эпоху Селевкидов появился специальный разделительный знак (прообраз нашего нуля), который ставился, если в числе был пропущен какой-нибудь шестидесятиричный разряд. Однако в конце числа этот знак никогда не ставился” [56], с.98.
Предлагаем в этих - и только в этих! - обозначениях-клинышках решить следующую “древне”-вавилонскую задачу. Решить (в рациональных числах или приближенно) систему из двух уравнений:
xy=6105,42.
“Вавилоняне первыми производили систематические наблюдения звездного неба, составляли календарь, вычисляли периоды обращения Луны и планет, могли предсказывать лунные и солнечные затмения” [56], с.99.
ВТОРАЯ ЗАДАЧА – “ДРЕВНЕ”-ВАВИЛОНСКАЯ.
Предлагаем - исключительно в терминах клинышков - рассчитать дату следующего солнечного затмения, которое будет видно в Санкт-Петербурге с фазой не менее 10.
НАШ КОММЕНТАРИЙ. По нашему мнению, описанный уровень развития «древне»-вавилонской науки – это на самом деле уровень XV-XVI веков н.э., когда ученые уже использовали удобные арабские цифры, владели понятием нуля и т.п.
ТРЕТЬЯ ЗАДАЧА «ДРЕВНЕ»-ГРЕЧЕСКАЯ.
Согласно скалигеровской истории, «древний» Диофант (якобы середина III века н.э.) успешно решал, например, следующую задачу [56], с.133-134. Найти все ПОЛОЖИТЕЛЬНЫЕ И РАЦИОНАЛЬНЫЕ решения следующей системы уравнений относительно неизвестных x1 и x2:
x1 + x2 = y
При этом, согласно скалигеровской истории, в эпоху Диофанта существовали специальные обозначения ЛИШЬ ДЛЯ ОДНОГО неизвестного и его степеней, до шестой включительно. Поэтому необходимо было заранее подобрать вид функции, например линейной или какой-нибудь другой, с помощью которой остальные неизвестные выражались через «основное неизвестное». Подчеркнем, что ЗНАК ПЛЮС вообще ОТСУТСТВОВАЛ [56], с.132-134. Поэтому положительные и отрицательные слагаемые группировались по отдельности и разделялись знаком «минус». Кроме того, ОТСУТСТВОВАЛО ПОНЯТИЕ НУЛЯ. И, наконец, ОТСУТСТВОВАЛИ ОБОЗНАЧЕНИЯ ДЛЯ ПАРАМЕТРОВ.
НАШ КОММЕНТАРИЙ. По нашему мнению, описанный уровень развития «древне»- греческой науки – это на самом деле уровень XVI-XVII веков н.э., когда ученые уже использовали удобные арабские цифры. Это – эпоха, непосредственно перед Кеплером. Именно в то время был изобретен НОЛЬ, знак ПЛЮС и т.д. Читатель, решивший описанную выше задачу с указанными ограничениями и в указанных «античных» обозначениях, поймет, что от Диофанта до современных алгебраических обозначений – всего один небольшой шаг.
ЧЕТВЕРТАЯ ЗАДАЧА – “ДРЕВНЕ”-ГРЕЧЕСКАЯ.
Согласно скалигеровской истории, “античный” Архимед успешно решил следующую задачу [56], с.124. Найти максимум следующего выражения:
Здесь α – конкретное число, x – переменная величина. При этом вы имеете право пользоваться лишь греческими буквенными обозначениями для цифр. ПОНЯТИЯ НУЛЯ ЕЩЕ НЕТ. Дифференциального исчисления тоже еще нет. Оно изобретено лишь в XVII-XVIII веках н.э. А НОЛЬ впервые по-настоящему появился лишь в конце XVI века. Тем не менее, как нас убеждают, «античный» Архимед жил якобы в III-II веках ДО н.э.
Недаром историки математики вынуждены отметить по поводу решения Архимедом указанной задачи следующее: «ТАКОГО ПОЛНОГО И ГЛУБОКОГО АНАЛИЗА МЫ НЕ ВСТРЕТИМ ДО XIX ВЕКА» [56], с.124.
В заключение предложим читателю также попытаться решить перечисленные выше “античные” задачи: используя лишь римские обозначения для цифр, то есть I, II, III, IV и так далее. Например, для начала выполните деление друг на друга двух чисел, записанных римскими символами. Если вы научитесь это делать, попробуйте рассчитать солнечное затмение в тех же обозначениях. Сразу скажем – ничего не получится. Проблемы возникнут уже при делении больших и рациональных чисел. Нужна символика, возникшая лишь в XVI-XVII веках.
ЯКОБЫ «ВОЗРОЖДЕНИЕ ПРОЦЕНТОВ» ЧЕРЕЗ ТЫСЯЧУ ЛЕТ
В журнале «Математика в школе», номер 5 за 2003 год, с.50-51, была опубликована статья О.О.Барабанова (Ковров) под названием «Задачи на проценты как проблема нормы словоупотребления». Открывается статья интересным введением «Из истории процентов». О.О.Барабанов отмечает: «В популярной литературе… возникновение этого термина (проценты – Авт.) связывается с внедрением в Европе десятичной системы счисления в XV в. Однако уже в «Дигестах Юстиниана», датируемых V в., мы находим ВПОЛНЕ СОВРЕМЕННОЕ УПОТРЕБЛЕНИЕ ПРОЦЕНТОВ. ««Фиск» не уплачивает проценты по заключенным им договорам, но сам получает проценты: например, от съемщиков публичных уборных, если эти съемщики слишком поздно вносят деньги; также при просрочке уплаты налогов. Когда же фиск является преемником частного лица, то обычно он уплачивает проценты. Если должники, платившие проценты в размере, меньшем чем 6% в год, стали должниками фиска, то они обязаны уплачивать 6% годовых того времени, как требование против них перешло к фиску»…
ПО-ВИДИМОМУ (комментирует эту цитату О.О.Барабанов – Авт.), ПРОЦЕНТ ВОЗНИК В ЕВРОПЕ ВМЕСТЕ С РОСТОВЩИЧЕСТВОМ, КАК ПРЕДТЕЧА ДЕСЯТИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ. РАЗРЫВ ВО ВРЕМЕНИ ЗАСТАВЛЯЕТ ВСПОМНИТЬ СОВРЕМЕННЫЕ ТЕОРИИ О ЛИШНИХ ВЕКАХ В ОБЩЕПРИНЯТОЙ ХРОНОЛОГИИ» (стр.50-51 указанной статьи).
Хотя О.О.Барабанов из каких-то соображений не упомянул наши фамилии и не дал ссылок на наши исследования, однако отмеченный им примерно ТЫСЯЧЕЛЕТНИЙ сдвиг во времени между возникновением якобы в V веке «античного процента» и затем якобы «возрождением процента» в XV веке, действительно практически совпадает с обнаруженным нами хронологическим сдвигом на 1000-1050 лет в скалигеровском «учебнике истории».
Картина абсолютно ясная. Идея процента впервые возникла в XV веке в связи с появлением ростовщичества, примерно в то же время, когда была внедрена десятичная система счисления. Затем часть финансовых средневековых документов была искусственно отброшена в далекое прошлое, где якобы в V веке и возник «процентный мираж».