Сronologia 3
di Anatoly T.Fomenko

PARTE PRIMA - LA DATAZIONE DELL'ALMAGESTO
di A. T. Fomenko, V. V. Kalashnikov e G. V. Nosovskiy.

testo tradotto in italiano da Claudio dell'Orda

This Italian translation of the fragments of the 3-st volume by Anatoly Fomenko was done by Claudio dell'Orda from the English edition: 
A. T. Fomenko, V. V. Kalashnikov, G. V. Nosovskiy
. History: " Fiction or Science?" Astronomical methods as applied to chronology. Ptolemy's Almagest. Tycho Brahe. Copernicus.
The Egyptian zodiacs.

CAPITOLO 3
I tentativi senza successo di datare l’Almagesto. I motivi dei fallimenti.
Il nostro nuovo approccio e un breve resoconto dei nostri risultati.

 

1. Il tentativo di datare l’Almagesto attraverso il confronto con i cataloghi calcolati che riflettono il moto delle stelle più veloci.
1.1. Il confronto tra il catalogo dell’Almagesto e i cataloghi calcolati.

Nel Capitolo 1 abbiamo descritto l'algoritmo per ricalcolare le posizioni moderne degli oggetti celesti indietro “nel passato”. Quindi, ciò che abbiamo a disposizione al momento è il catalogo dell'Almagesto compilato nelle coordinate dell'eclittica in un'epoca sconosciuta t_A e l'insieme {K(t)} dei cataloghi stellari calcolati. Riflettono la situazione effettiva sulla sfera celeste che abbiamo calcolato per un determinato momento t. Proviamo a determinare il valore desiderato della data t_A, ossia l'epoca in cui fu compilato il catalogo dell'Almagesto. Inizieremo con la seguente idea che sembra abbastanza semplice e proveremo a confrontare le posizioni delle singole stelle dell'Almagesto con le loro posizioni nei cataloghi calcolati K(t); dopodiché cercheremo di selezionare il valore t* per la valutazione della data tA, in modo che i dati dell'Almagesto corrispondano nel miglior modo possibile a quelli contenuti nel catalogo K(t*).

Ci asterremo dall'entrare nei dettagli sui criteri di qualità di quel genere di corrispondenze e ci limiteremo semplicemente a definire il significato di “confrontare l'Almagesto al catalogo K(t) con un dato valore t”. Quello che implica è selezionare le stesse coordinate dal catalogo K(t) e dall'Almagesto. Il confronto in questione fa sì che l'anno t serva per la presunta datazione delle osservazioni su cui si basa il catalogo dell'Almagesto. Pertanto, al fine di confrontare le coordinate delle stelle dell'Almagesto con le rispettive coordinate nel catalogo calcolato, si deve impostare l'eclittica dell'Almagesto sullo stesso piano dell'eclittica del catalogo calcolato K(t).
Tuttavia, questa sovrapposizione consentirà solo un confronto latitudinale, mentre noi abbiamo bisogno di confrontare anche le longitudini stellari. In altre parole, dovremo sovrapporre l’atlante stellare dell’Almagesto su quello vero per l’epoca t, supponendo che t sia il tempo effettivo di quando l’autore dell’Almagesto eseguì le sue osservazioni. Perciò bisogna segnare il punto dell’equinozio primaverile per l’epoca t sull’eclittica dell’Almagesto. Questo punto dovrà essere selezionato in modo tale che la media degli errori relativi alla longitudine per le stelle zodiacali dell’Almagesto sia uguale a zero. Tenete presente che per il nostro confronto con la longitudine delle stelle rilevanti nel catalogo K(t), stiamo usando la tabella delle identificazioni tradizionali delle stelle dell’Almagesto con la moderna carta astrale riportata in [1339]. Non è un compito formidabile selezionare il punto dell’equinozio. Come è noto (vedere [1040] e [1339]) t = 18,4 ossia corrisponde all’arco o segno dell’Ariete sull’eclittica dell’Almagesto per il 60 d.C., muovendosi alla velocità di circa 49,8” per ogni anno t, ovvero la velocità di precessione.

Non possiamo eludere del tutto gli errori, nella nostra scelta del punto dell'equinozio primaverile sull'eclittica dell'Almagesto con il metodo sopra indicato, che è statisticamente ottimale. La sua completa evasione sarebbe raggiunta se noi confrontassimo semplicemente le latitudini stellari senza prendere in considerazione le longitudini. Questo è ciò che faremo di seguito, nei Capitoli 3-5. Analizzeremo separatamente le latitudini e le longitudini. Le considerazioni riportate in questo paragrafo sono di carattere preliminare.

Figura 3.1. Il moto della vera stella Arturo rispetto alla sua posizione specificata nell'Almagesto.
Questo grafico non spiega l'errore sistematico commesso da Tolomeo, né lo compensa.



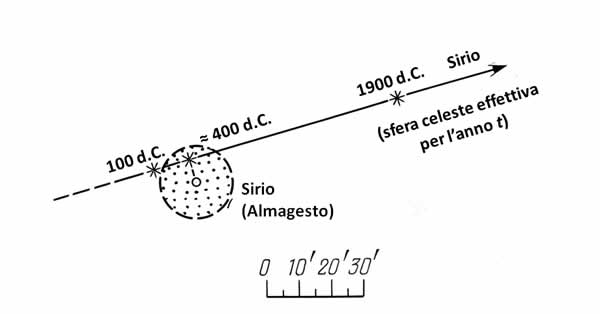
Figura 3.2. Il moto della vera stella Sirio rispetto alla sua posizione specificata nell'Almagesto. Questo grafico non spiega l'errore sistematico commesso da Tolomeo, né lo compensa.



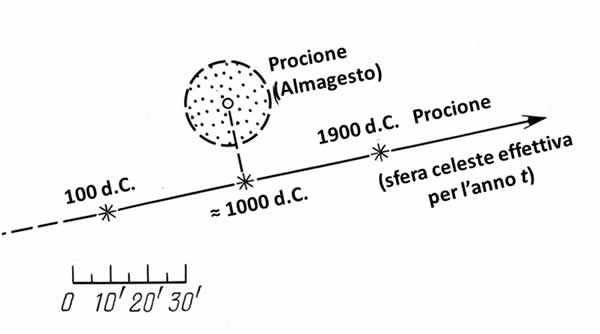
Figura 3.3. Il moto della vera stella Procione rispetto alla sua posizione specificata nell'Almagesto. Questo grafico non spiega l'errore sistematico commesso da Tolomeo, né lo compensa.

 

 

1.2. Il tentativo di datare il catalogo dell’Almagesto con i moti propri delle singole stelle.

Per il confronto scegliamo le nove delle stelle più veloci indicate nell'Almagesto secondo [1339]. Si tratta delle stelle la cui velocità di moto proprio supera 1" all'anno. L'elenco è il seguente:

α Cent (969) - 4.08" all'anno,

o² Eri (779) - 3,68" all'anno,

α Boo (110) = Arturo - 2.28" all'anno,

τ Cet (732) - 1,92" all'anno,

α CMa (818) = Sirio - 1.33" all'anno,

γ Ser (265) - 1,32" all'anno,

ι Per (196) - 1,27" all'anno,

α CMi (848) = Procione - 1.25" all'anno,

η Cas (180) - 1.22" all'anno.

Tutte queste stelle sono contenute nell'Almagesto in conformità alle identificazioni tradizionali ([1339]). I numeri dati a loro da Bailey nella numerazione seriale dell'Almagesto, sono tra parentesi. Rappresentiamo ciascuna di queste stelle dell'Almagesto come un cerchio senza ombreggiature, vedere le Figure dalla 3.1 alla 3.8. Abbiamo deciso di omettere α Centauri, dal momento che le coordinate di questa stella che si trova lontano a sud, nell'Almagesto vengono date con un gigantesco errore di 8 gradi. Nella Figura 3.4, a parte la stella 779 dell'Almagesto, si possono anche vedere le stelle vicine 778 e 780 e le traiettorie delle stelle reali numerate 1332, 1362 e 1363 nel catalogo ([1197]). Per cui, rimangono otto stelle. Ora consideriamo le piccole aree limitrofe di ognuna di queste otto stelle nell'atlante stellare di Tolomeo. Utilizzeremo le coordinate stellari indicate nell'Almagesto. Ognuna di queste aree contiene una delle otto stelle veloci elencate sopra. Inoltre, condividiamo l'opinione di [1339] che Tolomeo osservò effettivamente tutte le otto stelle e che queste sono davvero presenti nel suo catalogo.

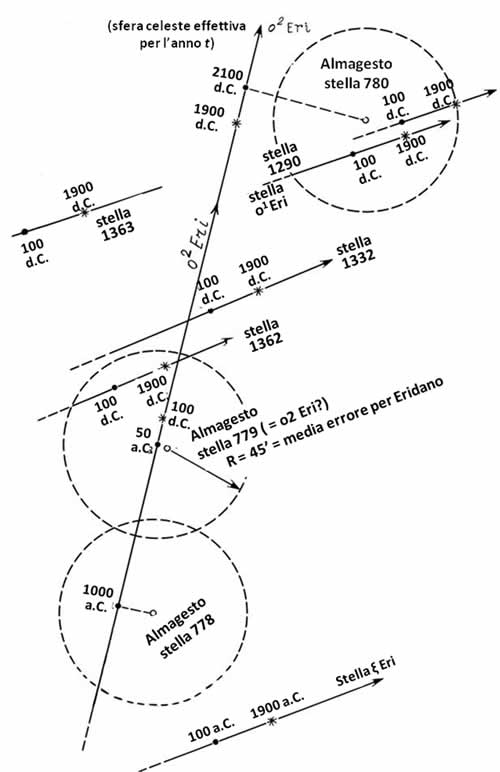
Figura 3.4. Il moto delle vere stelle o² Eri ed ξ Eri rispetto ai dati dell'Almagesto. Questo grafico non spiega l'errore sistematico commesso da Tolomeo, né lo compensa. I numeri delle stelle sono stati presi da un catalogo moderno ([1197]).



Figura 3.5. Il moto della vera stella η Cas rispetto alla sua posizione specificata nell'Almagesto. Questo grafico non spiega l'errore sistematico commesso da Tolomeo, né lo compensa.


Figura 3.6. Il moto della vera stella ι Per rispetto alla sua posizione specificata nell'Almagesto. Questo grafico non spiega l'errore sistematico commesso da Tolomeo, né lo compensa.


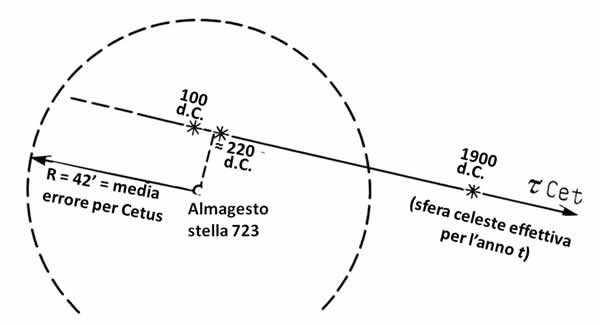
Figura 3.7. Il moto della vera stella τ Cet rispetto alla sua posizione specificata nell'Almagesto. Questo grafico non spiega l'errore sistematico commesso da Tolomeo, né lo compensa.


Figura 3.8. Il moto della vera stella γ Ser rispetto alla sua posizione specificata nell'Almagesto. Questo grafico non spiega l'errore sistematico commesso da Tolomeo, né lo compensa. I numeri delle stelle sono stati presi da un catalogo moderno ([1197]).

Ora sovrapponiamo l'atlante stellare compilato dal catalogo calcolato K(t), che riflette lo stato della vera sfera celeste per l'epoca t, sull'atlante stellare di Tolomeo compilato dall'Almagesto; utilizzeremo il metodo sopra descritto ed eseguiremo questa procedura per ogni epoca t. Ora disegneremo le nostre otto stelle veloci in mezzo alle stelle dell'Almagesto.

Il metodo per la sovrapposizione dell'atlante calcolato K(t) sull'atlante di Tolomeo, dipende dalla scelta dell'epoca t. Inoltre, ciascuna delle otto stelle veloci cambia posizione in relazione alle altre stelle prese dal catalogo calcolato K(t) con un'alterazione di t. Quindi, il modo in cui queste stelle saranno rappresentate sull'atlante di Tolomeo dipenderà anche dall'epoca t. Mostreremo anche le otto nuove traiettorie sull'atlante di Tolomeo che corrispondono allo spostamento delle nostre otto stelle veloci dopo l'alterazione di t. Queste traiettorie si possono vedere nelle Figure dalla 3.1 alla 3.8. Sottolineiamo che non stiamo ancora tenendo conto dell'errore sistematico nelle posizioni stellari, che abbiamo scoperto fu fatto dal compilatore dell'Almagesto. Più avanti descriveremo dettagliatamente la storia di questo errore.

Quali sono i periodi t che stiamo prendendo in considerazione, ora che le vere stelle veloci sono molto vicine a come furono rappresentate sull'atlante di Tolomeo?

In linea generale, questi momenti variano da stella a stella. Per le otto stelle sopra elencate, li segneremo con t₁, t2, ..., t₈. Se si dovesse scoprire che tutti i valori di ti (1 ≤ i ≤ 8), o che almeno molti di loro si rivelassero essere vicini l'uno all'altro, così come il valore medio di t*, questo sarebbe un forte argomento a favore della teoria che il periodo effettivo delle osservazioni dell'autore dell'Almagesto è prossimo a t*.

Tuttavia, non sembra proprio essere il caso. Infatti, i valori ti sono stati sparsi caoticamente nell'intervallo temporale - 70 ≤ t ≤ 30, ovvero il 1000 a.C. - 9000 d.C.! Lo spettro è davvero troppo grande. Abbiamo riportato i risultati nella Tabella 3.1 per renderli più illustrativi. Il fatto che le singole datazioni siano state distribuite in tutto questo enorme arco temporale, non è affatto una sorpresa. La questione è che ciascuna delle otto stelle messe a confronto è stata rappresentata nell'Almagesto con un errore piuttosto grave.

L'idea di una possibile percentuale di questo errore per una singola stella può essere ottenuta dalla declinazione media dell'arco nella costellazione di cui fa parte la stella in questione. Tramite la declinazione dell'arco riusciamo a comprendere il divario tra la posizione della stella nell'Almagesto e la sua vera posizione calcolata. A rigor di termini, l'errore medio indicato dipende dalla presunta datazione dell'Almagesto, per esempio a causa del veri moti delle stelle. Tuttavia, sulla sfera celeste le stelle sono per la maggior parte quasi immobili. Sembra che la percentuale di questo errore medio dipenda solo marginalmente dall'epoca in cui furono calcolate le coordinate stellari. Il livello di precisione che ci interessa, ci permette di ignorare questa dipendenza.

Per poter calcolare la percentuale media dell'errore, abbiamo usato la tabella di confronto che contiene le posizioni delle stelle nell'Almagesto, insieme al loro vere posizioni per il 130 a.C. che abbiamo trovato nel lavoro di Peters e Knobel ([1339]), cioè quelle calcolate per l'epoca del “antico" Ipparco. Disegniamo il “cerchio di precisione” attorno al punto che rappresenta una delle stelle veloci dell'Almagesto, il cui raggio sarà uguale al tasso medio dell'errore per la costellazione che contiene la stella in questione, vedere le Figure dalla 3.4 alla 3.8. La proiezione di questo cerchio sulla traiettoria della stella calcolata che riflette il moto di una stella veloce effettiva attraverso la sfera celeste, ci darà un'idea della possibile percentuale di errore pertinente alla datazione individuale ti della stella in questione rispetto alla data reale della compilazione del catalogo. Vogliamo inoltre sottolineare che gli errori di misurazione di una singola stella di cui non sappiamo nulla, possono differire drasticamente dalla percentuale media dell'errore. Il raggio del “cerchio di precisione” per Arturo, Procione, Sirio e le altre stelle denominate fu scelto pari a 10', ovvero il valore della scala graduata del catalogo dell'Almagesto. Vedere le Figure. 3.1, 3.2 e 3.3.

 

 

1.3. Perché la datazione dell’Almagesto attraverso i moti delle singole stelle ci ha dato dei risultati non affidabili?

La domanda che sorge inevitabilmente a questo proposito è se i risultati ottenuti con l'uso di una più delle otto stelle sopra elencate sono affidabili. In tal caso, sarà questa la stella o le stelle che dovremo usare allo scopo di valutare e datare la ricerca di Tolomeo, rifiutando così tutti quei dati che si basano su quelle stelle che non sono abbastanza affidabili? E' una cosa ovvia usare quelle stelle le cui coordinate sono le più corrette nell'Almagesto. Ma come si scelgono?

In alcune opere fu suggerito di valutare la precisione delle misurazioni di Tolomeo per ciascuna delle stelle in questione, basando il nostro giudizio sull'arco di discrepanza calcolato per una data stella, in altre parole l'ultima colonna della tabella riportata. Ad esempio, l'implicazione sarebbe che le coordinate della stella o² Eri furono misurate da Tolomeo con una precisione di 5', mentre quelle di Arturo con una precisione di 40'. Questo è esattamente ciò che fecero gli autori di [273] Y. N. Yefremov e Y. D. Pavlovskaya. Cercarono di datare l'Almagesto per mezzo dei moti propri e lavorarono nello specifico con lo stesso elenco di 9 stelle. Questo approccio produsse una datazione che si avvicinava a quella di Scaligero: il 50 a.C., vedere la Tabella 3.1. Valutare la possibilità che questa datazione sia errata è un problema separato che considereremo di seguito. Facendo un breve salto in avanti, vi diremo  semplicemente che in [273] il possibile tasso di errore del metodo di Yefremov e Pavlovskaya è stato valutato come perfettamente irrealistico.

Questo approccio ci porta immediatamente alla seguente serie di domande. La prima riguarda l'assurda situazione in cui tutte e tre le stelle di prima magnitudine tra le nove, vale a dire Arturo, Sirio e Procione (quelle che nel catalogo hanno un nome proprio) sono state misurati da Tolomeo molto grossolanamente, con tassi di errore che si avvicinavano a un grado intero. Eppure la stella o² Eri che è fioca e poco visibile, per qualche motivo venne misurata con la massima precisione e con una discrepanza pari a soli 5'! Vi spieghiamo che secondo le misurazioni moderne, la magnitudine di questa stella è pari solo a 4,5, il che significa che è molto fioca.

Tutto ciò è davvero molto bizzarro. Quelle stelle luminose e famose come Arturo, Procione, Regolo e Spiga, sono state usate da Tolomeo nella sua ricerca come dei punti di controllo, o perlomeno le loro coordinate furono misurate con la massima cura e precisione. La loro eccezionale importanza per l'antica astronomia si riflette nel fatto che nell'Almagesto hanno un nome proprio. Ci sono anche dei paragrafi  speciali dell'Almagesto che si occupano delle misurazioni di alcune di loro. Pertanto, la precisione di calcolo delle loro coordinate deve essere stata davvero molto elevata (vedi [968], ad esempio). Allo stesso tempo, non c'è niente di rilevante sulla stella o2 Eri. Non si riesce a distinguerla dalle stelle che la circondano, essendo anch'esse molto fioche.

Inoltre, la stella tradizionalmente associata ao² Eri viene semplicemente descritta nell'Almagesto come una “stella media”. Pertanto, dopo aver dato un'occhiata alla Figura 3.4, siamo giustificati a porci un'altra domanda perplessa. Perché la stella 779 dell'Almagesto potrebbe essere identificata con o² Eri? È perfettamente chiaro che questa è una conclusione a cui si può arrivare solo nel caso in cui le coordinate della vera stella o2 Eri e quelle della stella 779 dell'Almagesto siano correlate tra loro in modo ottimale: ad esempio, meglio di quelle tra o² Eri e la stella 778. Tuttavia, a causa della velocità significativa del moto proprio dio² Eri, ciò implica chiaramente che la sua identificazione con qualsiasi stella dell'Almagesto, dipende considerevolmente dall'epoca in cui dateremo l'Almagesto.

Ad esempio, se sapessimo che l'Almagesto fu scritto nel 1000 a.C., potremmo identificare o² Eri con la stella 778 dell'Almagesto e quindi “datare” con successo l'opera all'anno 1000 a.C., a giudicare dalla minima distanza possibile tra o² Eri e la stella 778, che servirebbe da “prova del fuoco” per la nostra datazione a priori.

A proposito, questa identificazione crea una concorrenza tra le coordinate di o² Eri e l'Almagesto, persino meglio della versione tradizionale, come si vede chiaramente nella Figura 3.4. Per esempio, se ipotizzassimo che l'Almagesto fu scritto nel 1500 d.C., ovvero nel XVI secolo, potremmo identificare la stella o² Eri con la stella 780 dell'Almagesto e datarla alla fine del Medioevo o persino in una “epoca futura”, vedere la Figura 3.4.

È ovvio che le riflessioni di questo tipo portano a un circolo vizioso. La datazione delle osservazioni basate sul moto proprio della stella necessita dell'identificazione affidabile di detta stella come contenuta nell'Almagesto, indipendentemente dalla sua presunta datazione.

Tuttavia, anche se dovessimo trascurare o² Eri, non potremmo comunque utilizzare le restanti otto stelle veloci per una datazione sicura. La dispersione delle datazioni è troppo grande per tutte le stelle differenti. Persino le datazioni fatte con le stelle di prima magnitudine tra le otto stelle in fase di studio (Arturo, Procione e Sirio) sono sparse nell'arco di 600 anni, tra il 400 d.C .e 1000 d.C., vedi la Tabella 3.1.

Inoltre, non bisogna dimenticarsi che le datazioni dedotte in quel modo (900 d.C. per Arturo) rappresentano solo i momenti in cui le posizioni reali delle stelle sono molto vicine a quelle fornite nel catalogo dell'Almagesto.

Inoltre, è necessario specificare gli intervalli di tempo che circondano queste datazioni, i cui valori di deviazione rientrerebbero in un intervallo conforme ai requisiti di precisione.

La gravità della situazione è così grande che se usassimo i valori medi per valutare quanto precisamente sono state misurate le stelle nell'Almagesto, commetteremo un errore a priori, in quanto non sappiamo nulla dei singoli errori commessi da Tolomeo nella misurazione delle stelle in questione.

Formuliamo il seguente corollario:

1. Ai fini della datazione, prima di poter usare le coordinate di una stella separata come indicate nell'Almagesto, bisogna assicurarsi che l'identificazione della stella in questione come una stella osservata sull'odierna sfera celeste, non dipenda da una presunta datazione dell'Almagesto, poiché ci condurrebbe di nuovo a un circolo vizioso.

2. Persino per le stelle più veloci, gli spostamenti dovuti ai moti propri sono abbastanza piccoli nella misura in cui è interessato l'intervallo del periodo storico (vedi le Figure dalla 3.1 alla 3.8). Pertanto, per la datazione occorre scegliere quelle stelle le cui posizioni nell'Almagesto sono state misurate con sufficiente precisione. Una stella che si sposta solamente di 2" in un anno, nell'arco di un secolo si sposterà di soli 3,3'.

Pertanto, se per la datazione dell'Almagesto volessimo utilizzare una singola stella veloce con un intervallo di precisione di circa 300 anni, dovremmo essere certi che la precisione della posizione di questa stella come indicata nell'Almagesto, non superi un tasso di discrepanza di 10'. Secondo le stime dei ricercatori, la precisione effettiva dell'Almagesto in linea generale è molto più bassa ([1339]).

Le stelle il cui tasso di discrepanza nella precisione delle coordinate supera i 20', sono inutili ai nostri scopi. L'intervallo di datazione minimo è di 1200 anni, se vogliamo usare quelle stelle a scopi di datazione.

Questo problema sarà considerato più nei dettagli di seguito (vedere i Capitoli 5 e 6).

 

 

 

2. Il tentativo di datare il catalogo dell’Almagesto attraverso un aggregato di stelle veloci e denominate, messe a confronto con i cataloghi calcolati.

2.1. Il criterio è quello di attenersi alla scelta delle stelle per scopi di datazione.

Nel paragrafo 1 abbiamo dimostrato che il confronto dell'Almagesto con i cataloghi calcolati K(t) per mezzo delle otto stelle più veloci, non ci consente di indicare un valore t* che correli nel miglior modo possibile l'Almagesto con il catalogo K(t*). Per ogni stella, il valore di t* = t*i è unico e differisce in modo significativo dai valori delle altre stelle. L'intervallo di dispersione per le diverse stelle è pari a diversi millenni. Pertanto, anche l'approccio sopra descritto è troppo approssimativo e non ci dà dei risultati sostanziali.

Tuttavia, potrebbe essere che una volta che abbiamo creato il campione, questo includa molto più che otto stelle, per cui dovremo elaborare un insieme di dati individuali {t*_i} la cui parte più grande cadrà in un intervallo di tempo piuttosto breve. In fin dei conti sarebbe sufficiente anche un intervallo di circa 500 anni; in questo caso avremmo una sorta di opportunità di ottenere le informazioni riguardanti la data effettiva della ricerca di Tolomeo (t_A). A parte questo, se riuscissimo a rendere il campione più inclusivo, questo potrebbe consentirci di utilizzare i metodi della matematica statistica per stimare il valore di t_A.

Quali altre stelle si dovrebbero includere nel campione? È chiaro che per la datazione si adattano solo le stelle veloci e misurate relativamente bene. Questi due criteri, la velocità del moto proprio e la precisione dei dati nell'Almagesto, in linea generale si completano a vicenda, poiché più veloce è la stella, maggiore sarà l'errore che potremmo fare con le sue coordinate nell'Almagesto, senza influenzare la datazione della stella in questione.

Queste considerazioni ci portano alla scelta delle seguenti stelle, per il confronto dell'Almagesto con i cataloghi calcolati K(t).

1. Le stelle che si muovono abbastanza velocemente. Scegliamo 0,5" come soglia di velocità annuale pertinente a una singola coordinata equatoriale di almeno α₁₉₀₀ e δ₁₉₀₀ per l'epoca del 1900 d.C., vedi la Tabella 1.1).
2. Le stelle “famose” o con un nome, oppure le stelle che hanno già dei vecchi nomi propri (cfr. la Tabella P1.2 nell'Appendice 1).

Naturalmente, le stelle denominate potrebbero aver ricevuto il nome già prima della creazione dell'Almagesto, cosa che sembra essere vera per molte stelle. Però, in primo luogo è improbabile che i nomi delle stelle siano stati dimenticati con l'età, anche se possono davvero essere stati alterati. In altre parole, le stelle con nome dell'epoca di Tolomeo sono rimaste tali fino ai giorni nostri. In secondo luogo, il fatto che una determinata stella abbia ricevuto un nome proprio, ci dice che è stata caricata di un significato particolare dalla vecchia astronomia. Sarebbe quindi di per sé implicito dire che Tolomeo prestò maggiore attenzione alle stelle con nome che alle altre e la cosa si manifesta particolarmente da una misurazione più precisa.

Scegliamo l'intervallo 0 ≤ t ≤ 30 come l’intervallo temporale a priori per la nostra ricerca (cioè, dal 1100 a.C. al 1900 d.C.). Tenete presente che la lettera t si riferisce al tempo contato a ritroso in secoli, a partire dal 1900 d.C.

 

2.2. Il sistema del “intervallo di prossimità” applicato a certe stelle veloci o con nome.

Uniamo gli elenchi delle stelle veloci e con nome dalle Tabelle P1.1 e P1.2 (dall'Appendice 1) per studiarli insieme. Sceglieremo quelle stelle dalle moltissime che secondo [1339] si trovano nell'Almagesto. L'elenco risultante sarà composto da circa 80 stelle. Calcoleremo la traiettoria di ogni stella di questo elenco nella griglia delle coordinate dell'Almagesto, come abbiamo fatto nel paragrafo 1 per le otto stelle più veloci.

Per essere sicuri di segnarle per questo scopo, abbiamo fissato un certo valore t come datazione presunta e calcolato la posizione di ciascuna stella per l'epoca t nelle coordinate eclittiche dell'epoca. Questa posizione può essere rappresentata con un punto sull'atlante stellare di Tolomeo, ovvero l'atlante costruito dal catalogo dell'Almagesto, supponendo che sia stato compilato nell'epoca t. Modificando il valore della presunta datazione all'interno dell'intervallo storico oggetto di studio, faremo muovere la stella, o il punto, lungo l'atlante di Tolomeo e attraverso le stelle dell'Almagesto. Come il tempo t si modifica, la stella calcolata i si muoverà attraverso le stelle dell'Almagesto (il moto proprio della stella e i lievi spostamenti dell'eclittica che avvengono nel corso del tempo). La distanza tra il punto o stella calcolata e la stella dell'Almagesto, che a sua volta cambia e viene identificata.

Le identificazioni corrispondono a [1339]. Le distanze sulla sfera celeste vennero misurata sull'arco geodetico che collega le stelle. Tenete presente che le linee geodetiche sulla sfera, ovvero la linea delle lunghezze brevi locali, sono gli archi delle grandi circonferenze o sezioni piane che attraversano il centro della sfera. Queste distanze sulle sfere sono chiamate distanze dell’arco; ci riferiremo semplicemente a loro con il termine di “distanze”.

Mettiamo che la distanza tra le stelle sia minima per il periodo t* = t_i. Abbiamo doppiato il momento t*, le “datazioni individuali” di una determinata stella nel paragrafo 1. Quando t si discosta dal valore t* in entrambe le direzioni, la distanza tra la stella effettiva calcolata e la sua rappresentazione nell'Almagesto inizia a crescere.

Consideriamo l'intervallo di datazione [t*₁, t*₂] = [t_i1,t_i2] dove la distanza in questione che non supera i 30' corrisponde a ogni stella con il numero i nell'elenco. Questo intervallo può effettivamente essere vuoto, che sarà il caso se la distanza tra la stella calcolata e la rispettiva stella dell'Almagesto superasse i 30' per il momento t. Il centro dell'intervallo sarà definito dal valore t*. Vedere la Figura 3.9.

Il limite di 30' per la distanza dell’arco tra la stella dell'Almagesto e la corrispondente stella calcolata, è stato scelto con l'obiettivo di far rimanere dentro la maggior parte delle stelle dell'Almagesto. Infatti, se dovessimo considerare il tasso medio quadratico dell’errore nella distanza dell’arco, affinché le stelle dell'Almagesto superino i 40' (che coincide con la ricerca condotta in [1339] e [614]), più della metà delle stelle dell'Almagesto sarebbero rappresentate con un tasso di precisione di circa 30'.

 

Figura 3.9. Il moto di una stella effettiva vicino alla posizione specificata per essa nell'Almagesto.

 

Ci stiamo basando sulle ipotesi della normale distribuzione degli errori e dell'indipendenza dell'errore, prese per le singole stelle. A causa della natura approssimativa del nostro discorso, le possibili discrepanze rispetto a queste presunzioni potrebbero non influire sui nostri corollari.

L'insieme degli intervalli che calcoleremo in questo modo, ossia gli “intervalli di prossimità”, li potete vedere nella Figura 3.10. Quello che vediamo qui è l'inizio dell'asse temporale con t = 0, ossia il 1900 d.C. e la fine con t = 30, ovvero il 1100 a.C. Ogni intervallo ha un centro definito dalla datazione ottimale per una data stella. Segniamo anche i punti per cui la distanza tra la “stella dell'Almagesto”, ossia la posizione fornita nell'Almagesto e la stella calcolata, saranno pari a 10' e 20' (vedi la Figura 3.9). Le linee che rappresentano le distanze sotto i 10' sono più spesse, come si vede nella Figura 3.10. Le estremità degli intervalli sono contrassegnate da frecce quando rimangono all'interno del grafico.

Molte delle stelle nel nostro elenco di quelle veloci e di quelle con nome, non hanno un intervallo corrispondente nella Figura 3.10. Ciò potrebbe implicare che l'intervallo in questione è:

1. Nel complesso inesistente (nei casi in cui la distanza tra la stella dell'Almagesto e la stella calcolata rimanga maggiore di 30').
2. Non riesce ad attraversare l'intervallo a priori 0 ≤ t ≤ 30 ed è situato oltre l'area del grafico.
3. Copre completamente l'intervallo a priori.

In quest'ultimo caso, le coordinate della stella devono essere misurate con sufficiente precisione per l'intervallo di 30'; tuttavia, non è possibile datare le osservazioni nell'intervallo tra il 1100 a.C. e il 1900 d.C. tramite le posizioni di tali stelle, poiché il loro moto è troppo lento.

Forniamo il numero di Bailey delle stelle dell'Almagesto, per le quali gli intervalli di prossimità di 30 minuti coprono l'intero intervallo 0 ≤ t ≤ 30 dato a priori (vedi [1339] e [1024]). Si trattano delle stelle con i numeri 35, 36, 163, 197, 222, 316, 318, 375 e 768.

Per molte stelle vengono forniti solo gli intervalli parziali. Ciò accade quando una parte dell'intervallo si trova all'esterno dell'intervallo a priori 0 ≤ t ≤ 30 e quindi non può essere raffigurato nella Figura 3.10.

Accanto a ciascun intervallo viene visualizzato il numero della corrispondente stella dell'Almagesto nella numerazione di Bailey. Il nome della stella moderna identificata come un'attuale stella dell'Almagesto, come pure il suo nome speciale (in caso ne abbia uno), viene riportato accanto al segno di uguale.

Nella Figura 3.12 raffiguriamo un grafico simile per le latitudini; il momento t = 18 è rappresentato da una linea tratteggiata e sta per la datazione di Scaligero dell'Almagesto (intorno al 100 d.C.).

 

2.3. E’ impossibile datare l’Almagesto con il metodo che suggerisce di utilizzare le distanze d'arco delle singole stelle.

La Figura 3.10 ci dice in modo molto esplicito che i valori del periodo t che appartengono simultaneamente a tutti gli intervalli di “massima prossimità”, non esistono. Alziamo la soglia di precisione che è iniziata con il valore di 30' scelto in precedenza, al fine di ottenere i valori desiderati di t. Gli intervalli visti nella Figura 3.10 crescono rispettivamente, con le frecce che indicano la direzione della crescita. Ad un certo punto, tutti gli intervalli devono iniziare a intersecarsi. Vediamo qual è il valore di t e il valore della soglia di precisione che sono necessari affinché si verifichi la prima intersezione. E' venuto fuori il valore t ≈ 12, ossia intorno al 700 d.C., con una soglia di precisione di circa 60', ovvero un grado. Se continuassimo ad alzare la soglia di precisione, l'intervallo di intersezione aumenterebbe in entrambe le direzioni dal punto t = 12.

Tuttavia, non possiamo considerare il punto t = 12 (il 700 d.C.) come stima sufficientemente affidabile della data in cui l'autore del catalogo dell'Almagesto realizzò le sue osservazioni, dal momento che l'intersezione di tutti gli intervalli di “massima prossimità” della Figura 3.10 avvengono con una soglia di precisione di 1 grado, il che implica l'esistenza in questo insieme delle stelle dell'Almagesto misurate malamente. L'errore nella stima della loro posizione contenuto nell'Almagesto, equivale come minimo a un grado.

Inoltre, se volessimo stimare la precisione delle coordinate stellari partendo dal basso con l'aiuto di un errore medio quadratico dell'arco nel punto ottimale t = 12, dovremmo aumentare il valore del tasso di accettabilità dell'errore (o soglia di precisione) di oltre 2 gradi. Tuttavia, quel valore della soglia di precisione farà in modo che l'intersezione dell'intervallo accettabile di “massima prossimità” copra l'intero periodo tra il 500 a.C. e il tempo presente (vedi la Figura 3.10). Questo corollario ha un interesse scientifico pari a zero, poiché è perfettamente comprensibile che l'Almagesto venne creato da qualche parte in questo vasto periodo.

Inoltre, la stessa datazione del 700 d.C. è piuttosto instabile nel seguente senso. Un'alterazione nell'insieme delle stelle in studio (che ovviamente è stato scelto piuttosto arbitrariamente) può spostare piuttosto significativamente il periodo di datazione. È chiaro che una situazione del genere rende nulle tutte le affermazioni riguardo una deduzione affidabile della data di compilazione del catalogo dell'Almagesto.

 

2.4. E’ impossibile datare l’Almagesto con il metodo che suggerisce di basarsi sulle discrepanze latitudinali delle singole stelle.

Figura 3.11. La discrepanza latitudinale tra la stella vera calcolata e la sua posizione specificata nell'Almagesto.

Consideriamo un altro metodo per calcolare gli intervalli di massima prossimità per le stelle dell'Almagesto dalla nostra lista delle stelle veloci e con nome. Questo metodo è simile a quello descritto in precedenza; la differenza è che questa volta la distanza tra la stella dell'Almagesto e la corrispondente stella calcolata, è composta dalla discrepanza latitudinale e non dai segmenti dell'arco. Per discrepanza latitudinale intendiamo la proiezione della lunghezza dell'intervallo che collega queste due stelle sulla griglia dei meridiani nelle coordinate dell'Almagesto (vedi la Figura 3.11). La scelta della discrepanza latitudinale (al posto di quella longitudinale, per esempio) è scaturita dalle seguenti considerazioni: in primo luogo, è risaputo che le latitudini delle stelle dell'Almagesto sono più precise delle longitudini (vedi [1339], per esempio, così come il Capitolo 2 del presente libro). In secondo luogo, la discrepanza latitudinale non dipende da come posizioniamo, in termini di longitudini, l'Almagesto in relazione al catalogo calcolato K(t), vedi il Capitolo 1. Pertanto, riusciremo a evitare di commettere ulteriori errori che possano derivare sia dalla giustapposizione che dalla possibile scelta arbitraria del punto iniziale di riferimento longitudinale (vedi Capitolo 1).

 

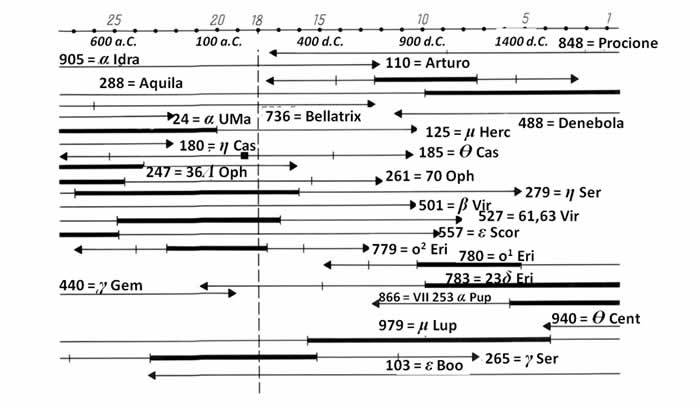
Figura 3.12. Gli intervalli di “massima prossimità latitudinale” tra stelle mobili visibilmente veloci o con un nome proprio e le corrispondenti “stelle dell'Almagesto”.

 

Nella Figura 3.12 possiamo vedere l'intervallo di massima prossimità risultante nel caso in cui la discrepanza latitudinale rappresenti la distanza. Ancora una volta, gli intervalli di prossimità che coprono l'intero intervallo 0 ≤ t ≤ 30, ovvero dal 1100 a.C. al 1900 d.C., sono assenti dal grafico. I numeri delle stelle dell'Almagesto per le quali gli intervalli di prossimità latitudinali di 30 minuti coprono completamente l'intervallo 0 ≤ t ≤ 30, sono i seguenti: 1, 35, 36,78, 111, 149, 163, 189, 222, 234, 287, 288, 315, 316, 318, 349, 375, 393, 410, 411, 424, 467, 469, 510, 713, 733, 760, 761, 768, 812 e 818.

Il confronto tra la Figura 3.12 e la Figura 3.10 dimostra che le longitudini delle stelle dell'Almagesto sotto esame sono davvero molto più precise delle loro posizioni sulla sfera celeste definite sia dalla latitudine che dalla longitudine. Questo è esattamente il motivo per cui si vedono più intervalli nella Figura 3.12 che nella Figura 3.10, in quanto rappresentano una maggior quantità di stelle.

Gli intervalli di massima prossimità per tutte le stelle nella Figura 3.12, a parte due stelle nel Centauro (935 = 2g Cent e 940 = 5θ Cent), iniziano a intersecarsi nel livello t = 12, ossia circa il 700 d.C., con una soglia di precisione latitudinale pari a 40'. Questo è un po' meglio rispetto al valore di 60' che abbiamo ottenuto nel caso precedente, ma non ancora abbastanza preciso. Siamo arrivati di nuovo alla datazione del 700 d.C. circa, ma come nel caso precedente non possiamo considerare affidabile questo risultato a causa delle considerazioni sopra riportate; perciò, questo metodo di datazione del catalogo non ci fornisce dei risultati tangibili.

In linea generale, a prescindere dal fatto che la transizione dalla discrepanza dell'arco alla discrepanza latitudinale ci aiuta in qualche modo a correggere gli errori dell'Almagesto e quindi ci consente di formulare corollari statistici più precisi, gli intervalli risultanti per le possibili datazioni rimangono troppo grandi. Coprono l'intero periodo del 4 ≤ t ≤ 20, ovvero dal 100 a.C. al 1500 d.C. Questi intervalli non ci forniscono informazioni utili in merito alla data delle osservazioni di Tolomeo.

 

 

 

3. Il tentativo di datare il catalogo dell’Almagesto attraverso il moto delle stelle individuali rispetto agli oggetti nelle loro immediate vicinanze.

3.1. La geometria variabile delle configurazioni stellari che si vedono sullo sfondo delle “stelle immobili”.

Nei paragrafi 1 e 2 abbiamo cercato di datare il catalogo con dei metodi approssimativi basati sulle varie configurazioni stellari che si sono alterate nel tempo a causa dei moti propri delle singole stelle che ne fanno parte. Abbiamo considerato individualmente ogni stella della configurazione, confrontando la sua posizione calcolata a quella fornita nell'Almagesto. Per confrontare tutte queste posizioni abbiamo dovuto usare la teoria di Newcomb che descrive il moto del sistema delle coordinate dell'eclittica utilizzato nell'Almagesto, che nel corso del tempo attraversa la “sfera delle stelle immobili”.

Vediamo quali risultati possiamo ottenere dal metodo di datazione dell'Almagesto che non utilizza la teoria di Newcomb. L'idea alla base di questo metodo è semplice. Non si devono confrontare le posizioni delle singole stelle sulla “vera” carta astrale calcolata teoricamente per le loro posizioni nell'Almagesto, ma piuttosto la geometria delle configurazioni stellari (che cambiano a causa dei moti propri delle stelle) con le configurazioni prese dal catalogo dell'Almagesto. L'unica cosa di cui abbiamo bisogno per questo confronto è la conoscenza dei valori di velocità del moto proprio delle singole stelle, non la teoria di Newcomb.

Sebbene gli errori risultanti dalla teoria di Newcomb siano piuttosto piccoli (molti ordini più piccoli del grado di valore del catalogo dell'Almagesto), dal punto di vista del calcolo lo studio delle configurazioni è molto più semplice in questo modo.

Oggigiorno i moti propri delle stelle vengono misurati con grande precisione, con l'aiuto delle osservazioni telescopiche ([1144] e [1197]). I valori dei moti propri delle stelle e la tabella che identifica le stelle dell'Almagesto con le loro controparti nelle moderne carte astrali, costituiscono gli unici dati che dobbiamo usare in questo caso. La tabella di identificazione è stata presa in prestito da [1339]; abbiamo omesso i casi ambigui indicati in essa.

 

3.2. Le stelle scelte per l’esperimento.

Continueremo a confrontare le posizioni di tutte le singole stelle che si muovono velocemente sulla vera carta stellare, con le loro posizioni specificate nell'Almagesto. Tuttavia, ora confronteremo le posizioni delle stelle sulla vera carta astrale e nell'Almagesto per un certo insieme di stelle referenziali. Per questo insieme abbiamo scelto sia le stelle con nome (Aldebaran, Scheat, ecc...) che quelle che spiccano sicuramente per luminosità tra le stelle che le circondano. Abbiamo escluso dall'elenco delle stelle referenziali quelle stelle le cui coordinate potrebbero essere state influenzate per mezzo della rifrazione. Sono state scelte complessivamente 45 stelle, tra cui quelle visibilmente mobili come Arturo, Sirio, Procione, Capella, Aquila = Altair, Denebola, Caph e Regolo. Pertanto, la posizione di una stella mobile sulla sfera celeste effettiva viene determinata in riferimento a una base mobile. L'immagine risultante cambia a seconda della presunta datazione e viene confrontata con la rispettiva immagine riflessa nell'Almagesto.

Come misura della deviazione prendiamo la discrepanza media di configurazione delle distanze dell'arco stellare:

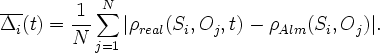
N indica la quantità delle stelle referenziali, ρ_real (S_i, O_j, t) è la distanza dell'arco tra la stella Si e la stella referenziale O_j sulla vera sfera celeste dell'epoca t. Inoltre, ρ_Alm (S_i, O_j) è la distanza dell'arco tra la stella S_i e la stella dell'Almagesto O_j. Il momento temporale t_i quando il valore di   (t) raggiungerà il suo minimo, sarà indicato come la datazione singola dalla stella in questione. Se i valori t_i delle datazioni singole per tutte le stelle veloci del catalogo dell'Almagesto, o almeno la loro maggioranza, cade in un intervallo di tempo sufficientemente breve, detto intervallo dovrebbe includere la vera data t_A delle osservazioni di Tolomeo, o essere situato nelle sue immediate vicinanze. Tuttavia, il vero status quo sembra essere completamente diverso.

Figura 3.13. Le singole discrepanze per le stelle mobili e la discrepanza media nelle otto configurazioni.
E' ovvio che non si possono trarre delle conclusioni definitive.

 

 

3.3. Il comportamento delle discrepanze singole e la discrepanza media.

Abbiamo studiato il comportamento delle discrepanze  (t) per le otto stelle veloci contenute nel catalogo dell'Almagesto, ovvero Capella (il numero di Bailey = 222), Arturo (110), Aquila = Altair (288), Denebola (488), Regolo (469), Sirio (818), Procione (848) e Caph (189).

Abbiamo deliberatamente scelto le più “famose” e le più brillanti tra le stelle veloci dell'Almagesto, e omesso quelle fioche. Come sottolineato sopra, nell'Almagesto le coordinate delle stelle più fioche possono essere rappresentate in modo molto impreciso. Pertanto, la loro inclusione nel campione potrebbe rendere molto più ampio l'intervallo di dispersione delle singole datazioni.

La Figura 3.13 mostra i grafici delle singole discrepanze per le stelle veloci indicate con  (t) come funzioni di t, e il grafico medio per tutte queste stelle. Sfortunatamente, nell'intero intervallo di tempo tra il 1100 a.C. e il 1900 d.C., questo grafico risulta essere piuttosto uniforme. (vedi la Figura 3.13).

 

3.4. Il risultato negativo dell’esperimento.

Il nostro rifiuto di usare la teoria di Newcomb non conduce alla concentrazione delle diverse datazioni per le singole stelle sull'asse temporale. L'implicazione è che i motivi di una così vasta gamma di singole datazioni non sono correlati al metodo di conversione applicato alle coordinate della sfera celeste, ma piuttosto si riferiscono alla bassa precisione delle coordinate fornita dal catalogo datato, dalla possibile eterogeneità del catalogo, ecc... Quest'ultimo potrebbe essere causato dalle diverse posizioni dell'eclittica durante le misurazioni eseguite nei diversi osservatori, che producono differenti errori sistematici per i vari gruppi di stelle.

Nel paragrafo 5 del presente capitolo analizzeremo le coordinate delle stelle dell'Almagesto e la struttura generale del catalogo dell'Almagesto, per scoprire tutti i fattori che potrebbero causarlo.