Глава 5.
АНАЛИЗ СИСТЕМАТИЧЕСКИХ ОШИБОК ЗВЕЗДНОГО КАТАЛОГА.
4. ИЗМЕНЕНИЕ ПАРАМЕТРОВ γstat(t) И φstat(t) С ТЕЧЕНИЕМ ВРЕМЕНИ.
Выше мы предполагали, что момент времени t фиксирован. Сейчас мы рассмотрим поведение найденных величин γstat и φstat в зависимости от времени.
Это поведение можно определить из формул, приведенных в предыдущем разделе. В них входят величины Li(t) и Bi(t), которые и порождают зависимость γstat и φstat от времени. Изменение долгот Li(t) и широт Bi(t) со временем - вещь хорошо изученная. См. главу 1. Соответствующие, достаточно громоздкие, расчеты проделаны нами с помощью компьютера при численном нахождении зависимостей оценок γstat(t) и φstat(t) от времени. См. главу 6. Здесь мы пока ограничимся анализом лишь качественного поведения этих функций.
Рассмотрим вновь звездную сферу и будем здесь считать для простоты, что все звезды на ней неподвижны. Таким образом, мы возвращаемся сейчас к представлениям Птолемея, хотя делаем это только ради упрощения рассуждений и выкладок. Мы можем так поступить, поскольку количество звезд, имеющих заметную скорость собственного движения, - то есть смещающихся на расстояние нескольких дуговых минут за рассматриваемый промежуток времени в 2500 лет, - сравнительно невелико. Наличие таких звезд практически не влияет на оценки параметров γstat(t) и φstat(t), которыми мы сейчас занимаемся.
На рис.5.4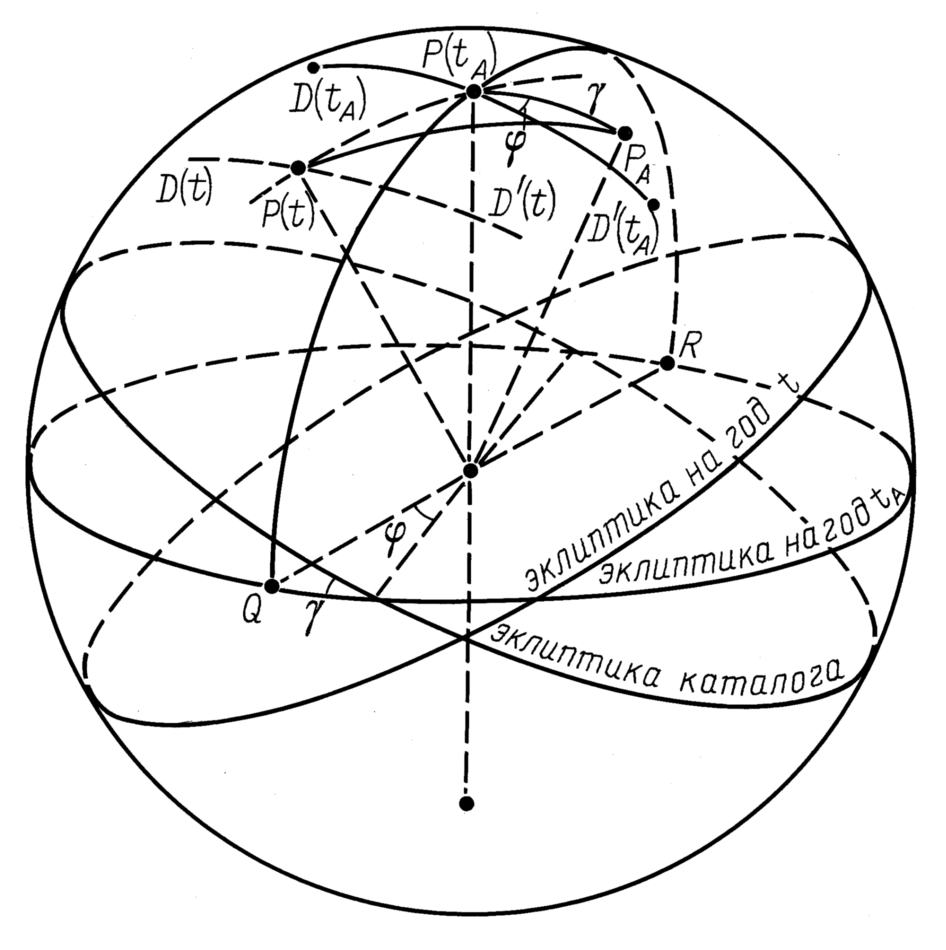
изображена звездная сфера и реальная эклиптика эпохи tA составления каталога. Полезно сравнить рис.5.1
и рис.5.4. В неизвестную нам эпоху tA полюс эклиптики P(tA) занимал некоторое, вполне определенное, положение на сфере. Составитель каталога конечно же отметил эклиптику на звездной сфере не идеально точно. Поэтому полюс PA отмеченной им "эклиптики каталога" занял положение, вообще говоря, отличное от P(tA).
Проведем через полюс P(tA) дугу большого круга, соединяющую его с точками весеннего равноденствия Q и осеннего равноденствия R. Дополнительно проведем через P(tA) дугу большого круга D(tA)D'(tA), пересекающую только что построенную дугу QP(tA)R под прямым углом в точке P(tA). Если бы дата tA была нам известна, то метод наименьших квадратов, описанный в разделе 3, позволил бы найти параметры γ и φ, определяющие взаимное расположение эклиптики эпохи tA и эклиптики каталога. Из рис.5.4 следует, что эти же углы определяют и взаимное положение полюсов P(tA) и PA на звездной сфере, а именно, величина γ равна длине дуги P(tA)PA, в дуговых величинах, а угол φ равен углу PAP(tA)D'(tA). С течением времени, как отмечалось в главе 1, положение эклиптики на звездной сфере изменяется. Это -- эффект колебания эклиптики. Поэтому полюс эклиптики в момент t, отличный от tA, окажется в точке P(t), также отличной от P(tA). Траектория полюса эклиптики на звездной сфере показана на рис.5.4 пунктирной линией, проходящей через точки P(t) и P(tA). И тогда, чтобы совместить эклиптику эпохи t и эклиптику каталога, нужно совместить полюса PA и P(t). Длина дуги P(t)PA равна величине γstat(t). Положение же оси вращения эклиптики, обеспечивающего данное совмещение, можно параметризовать углом PAP(t)D'(t), где дуга D(t)D'(t) "параллельна" дуге D(tA)D'(tA).
Чтобы разобраться в качественном поведении функций γstat(t) и φstat(t), обратимся к плоскому рисунку, где изобразим лишь перемещение полюсов эклиптики. Это допустимо, поскольку величины их смещений заведомо лежат в пределах одного градуса. Перенесем с рис.5.4 на плоскость картину вблизи северного полюса эклиптики, рис.5.5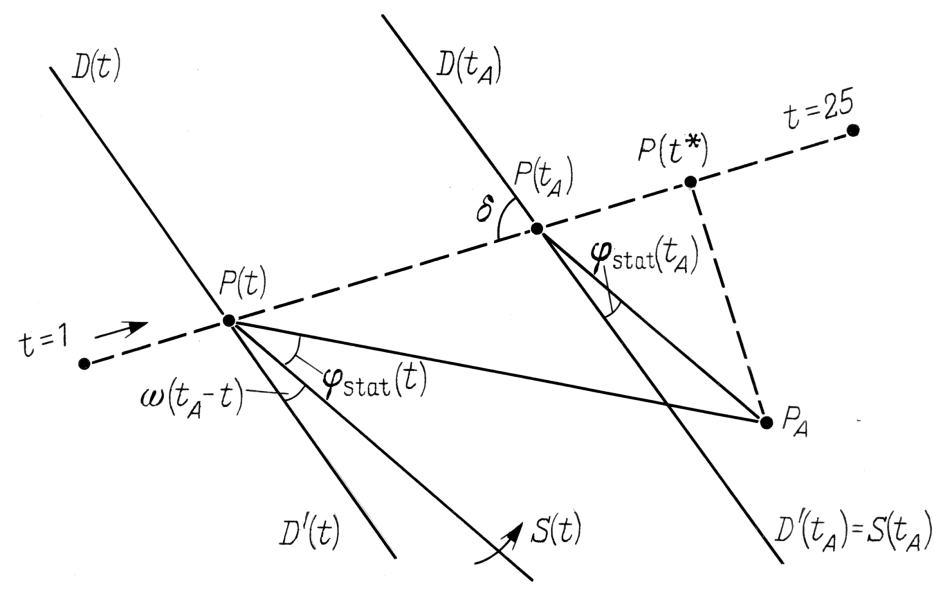
.
Как видно из рис.5.5, реальный полюс эклиптики с течением времени перемещается вследствие колебания эклиптики. На рассматриваемом интервале времени данное перемещение составляет всего около 25'. Поэтому его можно изобразить отрезком прямой. См. пунктирную прямую на рис.5.5. Движение полюса эклиптики вдоль этой прямой с большой точностью можно считать равномерным. Поэтому, например, расстояние между полюсами P(t) и P(tA) равно v(tA - t), где v -- скорость движения полюса эклиптики. Эта скорость равна приблизительно 0,01' в год. Как уже говорилось, в эпоху наблюдений tA, из-за ошибки в положении эклиптики, сделанной составителем каталога, полюс эклиптики каталога попал в точку PA, отличную от P(tA). Если при этом перпендикуляр, опущенный из точки PA на траекторию движения полюса эклиптики, пересек ее в точке t*>tA, как изображено на рис.5.5, то такая ошибка составителя, очевидно, "старит" эклиптику каталога, а именно, эклиптика каталога точнее всего будет отвечать эклиптике года t*. В противном случае, -- то есть если указанный перпендикуляр пересек траекторию в точке t*<tA, -- ошибка автора, напротив, "омолаживает" каталог. Чтобы дать представление о реальных соотношениях величин, укажем, что для Альмагеста расстояние между полюсом P(0) эклиптики на 1900 год н.э. и полюсом P(19) на начало нашей эры составляет около 20'. Приблизительно такое же значение имеет и ошибка γstat(tA).
Как было сказано, величина γstat(tA) равна длине отрезка P(tA)PA, а φstat(tA) -- углу PAP(tA)D'(tA). Аналогично, γstat(t) = P(t)PA. Здесь чертой сверху обозначена длина отрезка. Однако угол PAP(t)D'(t) не равен φstat(t), поскольку к моменту t ось весеннего равноденствия сместилась на величину ω(tA - t). Здесь ω -- угловая скорость прецессии, равная приблизительно 50'' в год. См. главу 1. Это смещение соответствует на рис.5.5 величине угла D'(t)P(t)S(t). Таким образом, φstat(t) = ∠ PAP(t)S(t), причем ∠ D'(t)P(t)S(t) = ω(tA - t).
Чтобы не использовать далее столь громоздкие обозначения, положим
| _______ | ________ | _______ |
| x(t) = P(t)P(tA), | y = P(tA)P(t*), | z = PAP(t*), |
| ψ(t) = ∠ PAP(t)D'(t), | δ = ∠ D(tA)P(tA)P(t). |
Величину γstat(tA) можно назвать ошибкой определения эклиптики. Для Альмагеста она имеет порядок 20'. Угол δ не зависит от t и равен углу между направлением движения полюса эклиптики и определенной ранее прямой D(tA)D'(tA). Очевидно, что
z = γstat(tA) sin(δ - φstat(tA)), \qquad\qquad y = γstat(tA) \cos(δ - φstat(tA)).
Поскольку x(t) = v(tA - t), то из рис.5.5 следует, что
Очевидно, что эта функция достигает минимального значения при t = t*. Если же рассматривается случай |t - tA| \ll |tA - t*|, то функция γstat(t) ведет себя практически как линейная:
γstat(t) ≈ γstat(tA) + v \cos(δ - φstat(tA))(tA - t).
Нетрудно найти также функцию φstat(t):
И вновь, если |t - tA| \ll |tA - t*|, можно воспользоваться линейным приближением:
Разумеется, найденные формулы дают лишь общее представление о характере функций γstat(t) и φstat(t). На рис.5.6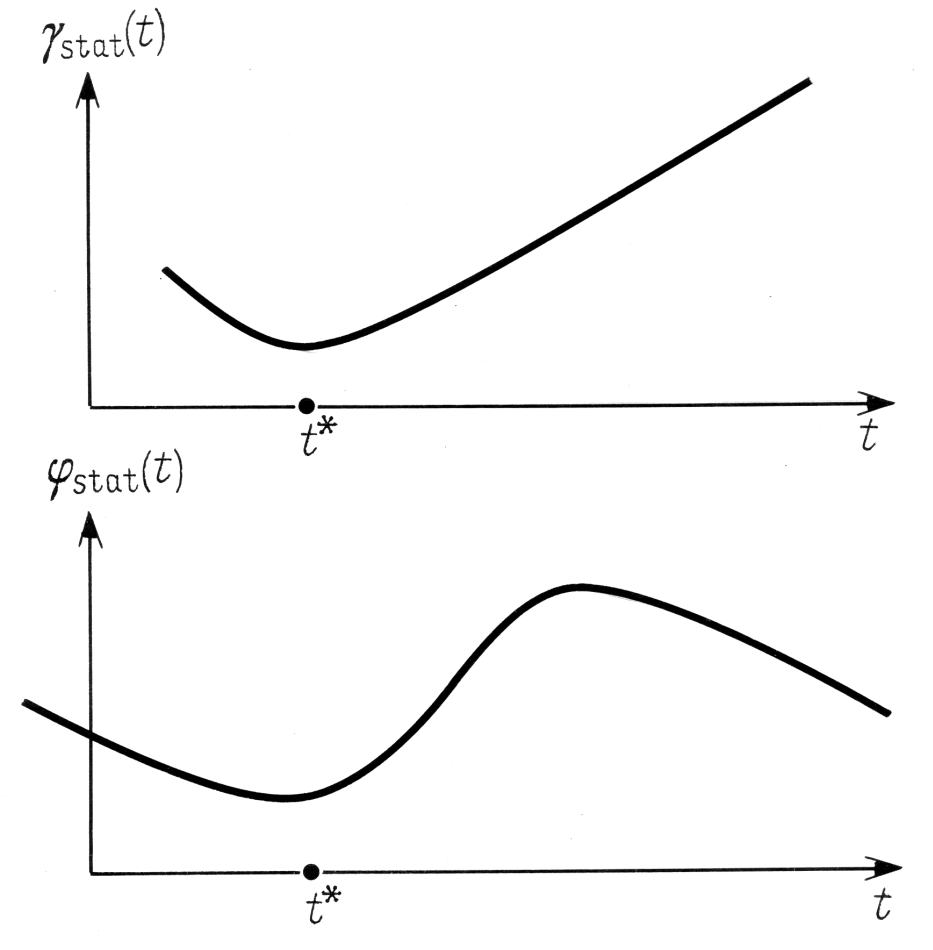
изображен примерный вид этих функций, получаемый из формул (5.4.1) и (5.4.2). Естественно, конкретный их вид зависит от значения ошибки, совершенной составителем каталога, то есть, от величин γstat(tA) и φstat(tA). Формулы (5.4.1) и (5.4.2) определяют также вид зависимости βstat(t). См. формулу (5.2.1).
Обсудим геометрический смысл данных построений. Рассмотрим птолемеевские координаты какой-либо группы звезд, считая что его наблюдения выполнены в момент времени t. В этом предположении, устраним систематическую ошибку φstat(t), γstat(t), то есть повернем всю группу звезд на угол γstat(t) вокруг оси, отстоящей от оси равноденствия на угол φstat(t)). Для простоты предположим, что систематическую ошибку мы нашли совершенно точно. Тогда полюс эклиптики каталога PA совместится с реальным полюсом P(t). Разумеется, после такого совмещения широтные невязки звезд все равно не станут равными нулю, так как в каталоге присутствуют еще случайные ошибки. Однако случайные ошибки, имея нулевое среднее, не смещают положение полюса эклиптики. Вернее, смещают ее лишь на малую величину, которая тем меньше, чем больше рассматриваемая совокупность звезд.
Из рис.5.5 видно, что перемещение полюса PA в точку P(t) разлагается единственным способом в композицию двух перемещений: PA → P(tA) и P(tA) → P(t). Параметры γstat(tA) и φstat(tA), задающие первое перемещение, имеют смысл ошибки наблюдателя, а именно -- той ошибки, которую совершил составитель каталога в определении положения плоскости эклиптики. Второе перемещение обусловлено вековым колебанием плоскости эклиптики. Это колебание можно рассчитать по теории Ньюкомба.
Из сказанного вытекает также следующий вывод. Обозначим через Δ Bi(t) широтную невязку i-й звезды, рассчитанную на момент t предполагаемых наблюдений, а через Δ Bi0(t) = Δ Bi(t) - γstat(t) sin(Li(t) + φstat(t)) -- ее широтную невязку на момент t после компенсации систематической ошибки. Тогда для совокупности, состоящей из полностью неподвижных звезд, величины Δ Bi0(t) не зависят от t и равны случайным ошибкам, допущенным Птолемеем при определении широт. Ситуация меняется, если в рассматриваемую совокупность входят подвижные звезды. Для них величины Δ Bi0(t) будут зависеть от времени t. Характер зависимости определяется как величинами индивидуальных случайных ошибок, так и направлением скоростей собственного движения звезд в совокупности. В частности, в неизвестную нам эпоху tA величина Δ Bi0(tA) равна случайной широтной ошибке для звезды i. Естественно ожидать, что если эта звезда быстро движется и, кроме того, хорошо измерена, то величина |Δ Bi0(t)| достигает минимума в окрестности точки tA. Величина этой окрестности зависит от величины и направления скорости собственного движения звезды и даже для самых быстрых звезд, например Арктура, составляет сотни лет.
Из приведенного выше рассуждения и, в частности, из рис.5.5, следует важный вывод. А именно, для определения полюса эклиптики каталога PA достаточно знать лишь два значения γstat, соответствующих различным значениям моментов времени t1 и t2.
В самом деле, из теории Ньюкомба нетрудно найти скорость перемещения полюса эклиптики v. См. главу 1. Зафиксируем два произвольных различных момента времени t1 и t2. См. рис.5.7
.
С помощью формулы (5.3.7) найдем значения γstat(t1) и γstat(t2). Изобразим прямую, по которой перемещается со временем полюс эклиптики. Отметим на ней точки t1 и t2. Выберем такой масштаб, чтобы расстояние между отмеченными точками равнялось v|t2 - t1|. Положение полюса эклиптики каталога PA определяется как точка пересечения двух окружностей с центрами в точках ti и радиусами γstat(ti), i=1,2. Из рис.5.7 ясно, как при этом определяются величины γstat(t) и φstat(t) для произвольного значения времени t. Необходимо лишь сказать, что прямая S'S, от которой отсчитывается угол φstat(t), пересекает траекторию движения полюса эклиптики под углом δ(t). Угол этот также находится из теории Ньюкомба. Астрономический смысл прямой S'S весьма нагляден. Это "спрямленная" часть большого круга звездной сферы, проходящего через полюс эклиптики P(t) эпохи t и перпендикулярного в точке P(t) другому большому кругу, также проходящему через P(t) и точки равноденствия эпохи t.
Аналогично, для определения параметров γstat(t) и φstat(t) при всех t достаточно знать лишь два значения: φstat(t1) и φstat(t2).
Мы, однако, будем работать с углом γ. Он имеет содержательный смысл: это -- ошибка в определении угла наклона между плоскостями экватора и эклиптики. Заметим, что этот угол фиксируется, например, в армиллярной сфере. Следовательно, ошибка γ, допущенная в этом угле, может являться инструментальной ошибкой армиллярной сферы. См. главу 1. Таким образом, ошибка γ естественным образом возникает при астрономических измерениях. Кроме того, выбор γ в качестве параметра будет нами далее обоснован и со статистической точки зрения.
