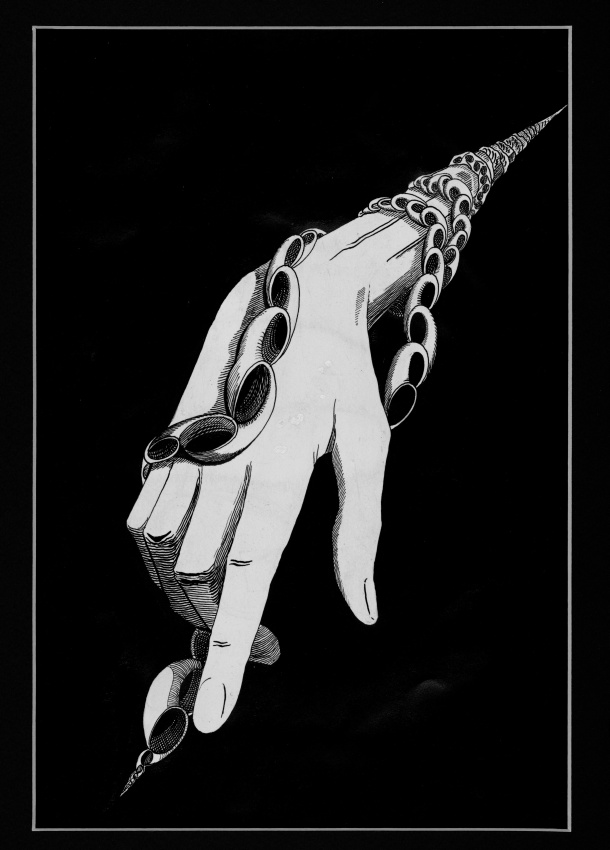
A space with nontrivial local homology
No. 8, 1967 (Topology, homology theory)
India ink on paper, 21.5x32.5 cm.
Reaching from infinity and pointing to another faraway infinity, (1 lanky hand finds itself coiled by a polyhedron, composed of an infinite band of shells all glued together, each bonded to another at a single point, creating an infinite chain. Notice that to cut this infinite polyhedron in any one place, any arbitrary place, would mean cutting at least one shell, creating a hole. Such a hole is nontrivial. In fact, it is a one-dimensional cycle—a surface without boundary—that could not, for instance, sustain spanning by a film.
Notice too that the base opening of each shell is sealed by the spiral of the next shell, a fact that gives this shape some of its peculiar and remarkable properties. Finally, see now that the shells decrease in size as they wind their way toward two singular points that designate the destination, the two infinities.