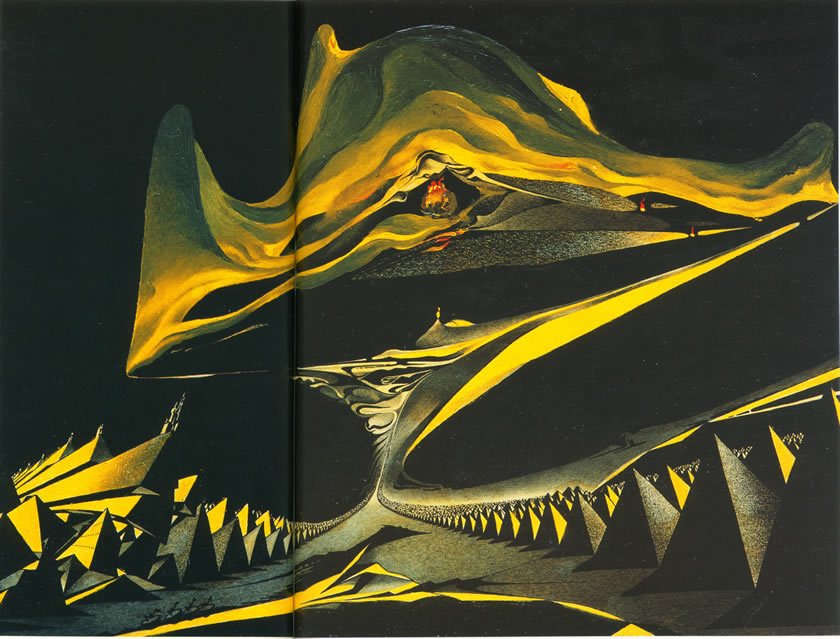
Combinatorial contractio
No. 75, 1973
(Combinatorial topology)
India ink, pencil, and oil on paper, 30.5x43 cm.
In this dark, angular world, spiky pyramids align on an infinitely deep wall, juxtaposed with organic, undulating shapes. Underlying this image is an intuitive representation, a certain view of an operation known as a combinatorial contraction of a polyhedron. If the polyhedron contains a simplex with a free face, a face to which no other simplex is attached, then we can remove this tetrahedron without changing its homotopic type. In other words, by pressing the free face into the tetrahedron, we actually eat it up, leaving only those faces that are hooked to other tetrahedra. In this image, we see frozen in time an intermediate moment of the combinatorial contraction, before all of the three-dimensional simplexes have gone away. Only the central region is free of them. The free faces of the tetrahedra form a boundary of the three- dimensional polyhedra. In the topology of three-dimensional manifolds, this process often comes up when constructing spines of a manifold with a boundary.