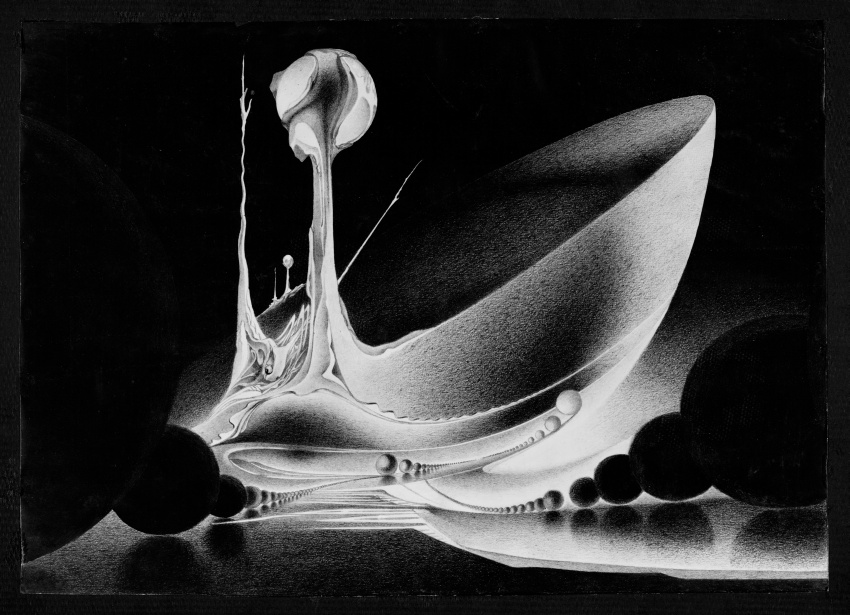
Interior and boundary points of a manifold and symmetric spaces
No. 80, 1972
(Theory of manifolds)
India ink and pencil on paper, 31x43 cm.
A meditation on spheres. Stretched out along a deep flat surface, spheres are aligned in columns that reach back toward infinity. At center, a sphere is undergoing a transformation, becoming a sculpture, on whose edge grows a creature with arms that reach toward the sky. Dark brightens into light, one form grows out of another, and together they create a magnificent scene of rounded shapes. Here, these objects highlight the difference between the points on the interior and the points on the boundary of a manifold. By gluing together standard Euclidean balls and half-balls, we are able to create a manifold with boundary. Indeed, the sculpture poised on the edge of the large half-ball prevents it from being invariant under rotations about its central axis.