А.Т.Фоменко
ЧИСЛА ПРОТИВ ЛЖИ

Глава 5.
МАТЕМАТИКО-СТАТИСТИЧЕСКИЕ МЕТОДЫ ДАТИРОВАНИЯ ДРЕВНИХ СОБЫТИЙ.

3. ПРИНЦИП ЗАТУХАНИЯ ЧАСТОТ. МЕТОД УПОРЯДОЧИВАНИЯ ИСТОРИЧЕСКИХ ТЕКСТОВ ВО ВРЕМЕНИ.

Принцип затухания частот и основанный на нем метод предложен и разработан мною в [884], [886], [888], [1129], [891], [895], [898], [901], [1130].

Настоящий метод позволяет находить хронологически правильный порядок отдельных фрагментов текста, обнаруживать в нем дубликаты на основе анализа, например, совокупности собственных имен, упомянутых в тексте. Как и в предыдущих методиках, мы стремимся к созданию метода датировки, основанного на численных, количественных характеристиках текстов и не обязательно требующего анализа смыслового содержания текстов, которое может быть весьма многозначно и расплывчато.

Если в документе упомянуты какие-либо "знаменитые", ранее известные нам персонажи, описанные в других, уже датированных хрониках, то это позволяет датировать описанные в тексте события. Однако если такое отождествление сразу не удается и если, кроме того, описаны события нескольких поколений с большим количеством ранее неизвестных действующих лиц, то задача установления тождества персонажей с ранее известными усложняется. Для краткости назовем фрагмент текста, описывающий события одного поколения, "главой-поколением".

Будем считать, что средняя длительность одного "поколения" - это средняя длительность правления реальных царей, зафиксированных в дошедших до нас летописях. Эта средняя длительность правления царей вычислена автором настоящей книги при обработке хронологических таблиц Блера [76]. Она оказалась равной 17,1 года [884].

При работе с реальными историческими текстами выделение в них "глав-поколений" иногда наталкивается на трудности. В таких случаях мы ограничивались лишь приблизительным разбиением текста на последовательные фрагменты. Пусть летопись Х описывает события на достаточно большом интервале времени (А,В), на протяжении которого сменилось по крайней мере несколько поколений персонажей. Пусть летопись Х разбита на "главы-поколения" Х(Т), где Т - порядковый номер поколения, описанного во фрагменте Х(Т) в той нумерации "глав", которая фиксирована в тексте.

Возникает вопрос: правильно ли занумерованы, упорядочены эти "главы-поколения" в летописи? Или же, если эта нумерация утрачена или сомнительна, то как ее восстановить? Другими словами, как правильно расположить во времени "главы" друг относительно друга? Оказывается, для реальных исторических текстов в подавляющем большинстве случаев выполняется следующая "формула"-правило: полное имя = персонаж. Это означает следующее.

Пусть интервал времени, описываемый летописцем, достаточно велик, например, составляет несколько десятков или сотен лет. Тогда, - как было проверено нами в результате анализа большого набора исторических документов, - в подавляющем большинстве случаев РАЗНЫЕ ПЕРСОНАЖИ имеют в одном и том же тексте РАЗНЫЕ ПОЛНЫЕ ИМЕНА. Полное имя может состоять из нескольких слов, например, Карл Плешивый. Другими словами, ЧИСЛО РАЗНЫХ ЛИЦ С ОДИНАКОВЫМИ ПОЛНЫМИ ИМЕНАМИ НИЧТОЖНО МАЛО' ПО СРАВНЕНИЮ С КОЛИЧЕСТВОМ ВСЕХ ПЕРСОНАЖЕЙ. Это верно для всех нескольких сотен исследованных нами исторических текстов, описывающих Рим, Грецию, Германию, Италию, Россию, Англию и т.д. Ничего удивительного в этом нет. В самом деле, летописец заинтересован в различении разных персонажей, чтобы избежать путаницы. Простейший способ добиться этого - присвоить разным лицам разные полные имена. Это простое психологическое обстоятельство и подтверждается подсчетами.

Сформулируем теперь ПРИНЦИП ЗАТУХАНИЯ ЧАСТОТ, описывающий хронологически правильный порядок "глав-поколений".

При правильной нумерации "глав-поколений" летописец, ПЕРЕХОДЯ ОТ ОПИСАНИЯ ОДНОГО ПОКОЛЕНИЯ К СЛЕДУЮЩЕМУ, СМЕНЯЕТ И ПЕРСОНАЖЕЙ. А именно, при описании поколений, предшествующих поколению с номером Q, он ничего не говорит о персонажах этого поколения, так как они еще не родились. Затем, при описании поколения Q, летописец именно здесь больше всего говорит о персонажах этого поколения, поскольку с ними напрямую связаны описываемые им события. Наконец, переходя к описанию последующих поколений, летописец все реже и реже упоминает о прежних персонажах, так как описывает новые события, персонажи которых вытесняют умерших.

Здесь важно подчеркнуть, что мы имеем в виду не какие-то отдельные имена, а полный резервуар всех имен, использовавшихся в поколении с номером Q.

Вкратце наша модель формулируется так. КАЖДОЕ ПОКОЛЕНИЕ РОЖДАЕТ НОВЫЕ ИСТОРИЧЕСКИЕ ЛИЦА. ПРИ СМЕНЕ ПОКОЛЕНИЙ ЭТИ ЛИЦА СМЕНЯЮТСЯ.

Несмотря на внешнюю простоту, этот принцип оказался полезен при создании метода датировки. Принцип затухания частот имеет эквивалентную переформулировку. Так как персонажи практически однозначно определяются своими полными именами (имя = персонаж), то мы будем изучать резервуар всех полных имен текста. Термин "полное" будем обычно опускать, постоянно подразумевая его. Более того, оказалось, что подавляющее большинство исторических имен являются "простыми", состоящими из одного слова. Поэтому при обработке больших исторических текстов со значительным запасом имен можно рассматривать лишь "элементарные имена - кирпичи", разбивая редкие полные имена на отдельные составляющие их слова.

Рассмотрим группу всех имен, впервые появившихся в тексте, в "главе-поколении" с номером Q. Условно назовем эти имена Q-именами, а соответствующие им персонажи Q-персонажами. Количество всех упоминаний, с кратностями, всех этих имен в данной "главе" обозначим через K(Q,Q). Подсчитаем затем, сколько раз эти же имена упомянуты в "главе" с номером Т. Получившееся число обозначим через K(Q,T). При этом, если одно и то же имя повторяется несколько раз, то есть с кратностью, то все эти упоминания подсчитываются. Построим график, отложив по горизонтали номера "глав", а по вертикали - числа K(Q,T), где номер Q - фиксирован, а T - меняется. Для каждого Q мы получаем свой график. Принцип затухания частот тогда формулируется так.

При хронологически правильной нумерации "глав-поколений" каждый график K(Q,T) должен иметь следующий вид. СЛЕВА ОТ ТОЧКИ Q ГРАФИК РАВЕН НУЛЮ, В ТОЧКЕ Q - АБСОЛЮТНЫЙ МАКСИМУМ ГРАФИКА, ПОТОМ ГРАФИК ПОСТЕПЕННО ПАДАЕТ, БОЛЕЕ ИЛИ МЕНЕЕ МОНОТОННО ЗАТУХАЕТ, рис.5.24.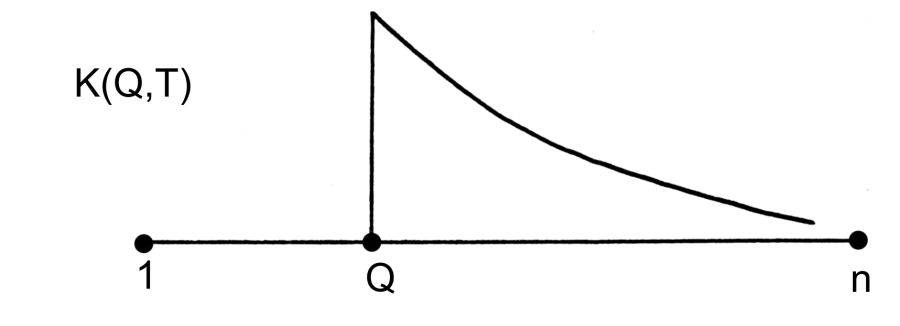

Этот график на рис.5.24 мы назовем идеальным. Сформулированный принцип должен быть проверен экспериментально. Если он верен и если "главы" в летописи упорядочены хронологически правильно, то все экспериментальные графики должны быть близки к идеальному. Проведенная экспериментальная проверка полностью подтвердила принцип затухания частот [904], [908]. Приведем некоторые типичные примеры.

 

4. ПРИМЕНЕНИЕ МЕТОДА К НЕКОТОРЫМ КОНКРЕТНЫМ ИСТОРИЧЕСКИМ ТЕКСТАМ.

ПРИМЕР 1. "Римская история" Тита Ливия, М., 1887-1889, тт.1-6. Все графики K(Q,T) для частей "Истории", описывающих периоды 750-500 годы до н.э. и 510-293 годы до н.э., оказались практически тождественными с идеальным. То есть, подавляющее большинство имен, впервые появившихся в описании Тита Ливия в каком-то поколении, наиболее часто упоминаются Титом Ливием при описании именно этого поколения, а затем постепенно утрачиваются, забываются. Следовательно, принцип затухания частот подтверждается, и относительный порядок "глав-поколений" внутри указанных частей "Истории" Тита Ливия скорее всего хронологически правилен. И напротив, при сравнении двух указанных частей текста Тита Ливия друг с другом, обнаруживается, что здесь принцип затухания частот не выполняется. Это может указывать, что внутри "Истории" Тита Ливия присутствуют дубликаты, повторы.

ПРИМЕР 2. Liber Pontificalis, см. [196], изд. Т.Моммзена, Gestorum Pontificum Romanorum, 1898. Это - известная "Книга (римских) Пап (понтифексов)". Выделим из этого набора текстов куски, описывающие периоды: 1) 300-560 годы н.э., 2) 560-900 годы н.э., 3) 900-1250 годы н.э., 4) 1250-1500 годы н.э.

Оказывается, все частотные графики K(Q,T) для указанных текстов 1-4 практически совпадают с идеaльным, что подтверждает принцип затухания частот и правильность относительного расположения "глав" внутри каждого из перечисленных исторических фрагментов.

Отметим одно из следствий проведенного эксперимента. На значительных временны'х интервалах, оказывается, НЕ БЫЛО "МОДЫ НА ДРЕВНИЕ ИМЕНА". Что само по себе отнюдь не очевидно. Конечно, отдельные древние имена употребляются и сегодня, например Петр, Мария и т.д. Но, как мы обнаружили, либо эти имена не являются полными, либо процент таких "выживших древних" имен очень мал по сравнению с основной массой "вымирающих" имен. Наличие редких "выживших" имен означает, что экспериментальные графики K(Q,T) падают при движении слева направо не до нуля, а до некоторой ненулевой постоянной.

ПРИМЕР 3. В качестве текста Х, описывающего период 976-1341 годы н.э. в истории Византии, мы взяли следующие первоисточники:

1) Михаил Пселл, "Хронография", М., 1987. Описывает период 976-1075 годы.

2) Анна Комнина, "Сокращенное сказание о делах царя Алексея Комнина" (1081-1118 годы), СПБ, 1859.

3) Иоанн Киннам, "Краткое обозрение царствования Иоанна и Мануила Комнинов" (1118-1180 годы), СПБ, 1859.

4) Никита Хониат, т.1, "История, начинающаяся с царствования Иоанна Комнина" (1118-1185 годы), СПБ, 1860.

5) Никита Хониат, т.2, "История со времени царствования Иоанна Комнина" (1186-1206 годы), СПБ, 1862.

6) Георгий Акрополит, "Летопись" (1203-1261 годы), СПБ, 1863.

7) Георгий Пахимер, "История о Михаиле и Андронике Палеологах" (1255-1282 годы), СПБ, 1862.

8) Никифор Григора, "Римская история" (1204-1341 годы), СПБ, 1862.

Мы обработали все эти тексты, выделив из них все собственные имена и подсчитав распределение частот их упоминаний. Указанный набор текстов содержит несколько десятков тысяч упоминаний полных имен, с кратностями. Оказалось, что все частотные графики K(Q,T) на интервалах 976-1200 годы и 1200-1341 годы практически тождественны с идеальным. Таким образом, и здесь принцип затухания частот оказался выполненным. А с другой стороны, выяснилось, что хронологический порядок текстов внутри каждого из указанных интервалов времени правилен.

ПРИМЕР 4. Ф. Грегоровиус, "История города Рима в средние века", СПБ, тт.1-6, 1902-1912. Из этого текста были выделены куски, описывающие: 1) 300-560 годы н.э., 2) 560-900 годы н.э., 3) 900-1250 годы н.э., 4) 1250-1500 годы н.э.

Каждый из фрагментов был разбит на "главы-поколения". Мы выделили все собственные имена и проследили частоты их упоминаний. Полный резервуар имен насчитывает здесь несколько тысяч упоминаний. Оказалось, что принцип затухания частот верен и упорядочивание "глав" в каждом из текстов 1-4 хронологически правильно.

Аналогичный результат получен и для монографии Кольрауша "История Германии", М., тт.1-2, 1860, в которой были выделены куски, описывающие: 1) 600-1000 годы н.э., 2) 1000-1273 годы н.э., 3) 1273-1700 годы н.э.

 

5. МЕТОД ДАТИРОВАНИЯ СОБЫТИЙ.

Всего нами было обработано несколько десятков больших исторических текстов. Во всех случаях, когда тексты описывают события эпохи XVI-XX веков, принцип затухания частот подтвердился. Отсюда вытекает методика хронологически правильного упорядочивания "глав-поколений" в тексте, или в наборе текстов, где порядок нарушен или неизвестен. Рассмотрим совокупность "глав-поколений" летописи Х и занумеруем их в каком-нибудь порядке. Для каждой "главы" X(Q) подсчитаем число K(Q,T) при заданной нумерации "глав". Все числа K(Q,T), при переменных Q и T, естественно организуются в квадратную матрицу К{Т} размера n х n, где n - общее число "глав". В идеальном теоретическом случае частотная матрица К{Т} имеет вид, показанный на рис.5.25.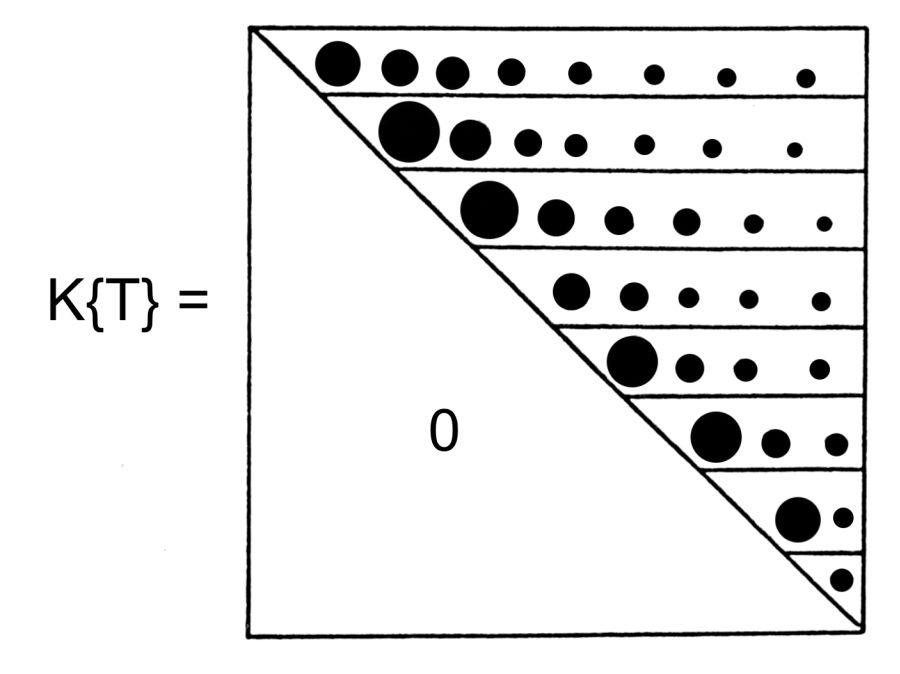

На рис.5.25 ниже главной диагонали стоят нули, на главной диагонали расположен абсолютный максимум в каждой строке. Затем каждый график, в каждой строке, монотонно падает, затухает.

Оказывается, аналогичная картина затухания наблюдается и для столбцов матрицы. Это означает, что частота употребления в "главе" X(Q) имен более раннего происхождения "в среднем" тоже падает по мере удаления поколения T, породившего эти имена, от фиксированного поколения Q. Для оценки скорости затухания частот удобно пользоваться усредненным графиком

Kсред.(T) =	сумма величин K(Q,P), где P-Q=T -------------------------------------------------------
	n-T

В этой формуле суммирование выполняется по всем парам (Q,P), для которых разность P-Q фиксирована и равна T. Другими словами, график K_сред.(T) получается усреднением матрицы K{T} по ее диагоналям, параллельным главной. Он изображает "усредненную строку" или "усредненный столбец" частотной матрицы. Здесь T изменяется от 0 до n-1. Конечно, экспериментальные графики могут не совпадать с теоретическим.

Если теперь изменить нумерацию "глав" в летописи, то изменятся и числа K(Q,T), поскольку возникает довольно сложное перераспределение "впервые появившихся имен". Следовательно, меняется частотная матрица К{Т} и ее элементы. Будем менять порядок "глав" летописи с помощью различных перестановок s. Каждый раз вычислим новую частотную матрицу К{sТ}, где sТ - новая нумерация, соответствующая перестановке s. Будем искать такой порядок "глав" летописи, при котором все или почти все графики будут иметь вид, показанный на рис.5.24. В этом случае экспериментальная частотная матрица К{sТ} будет наиболее близка к теоретической матрице на рис.5.25. Тот порядок "глав" летописи, при котором отклонение экспериментальной матрицы от "идеальной" будет наименьшим, и следует признать хронологически правильным и искомым.

Наш метод позволяет также датировать события. Пусть дан какой-то исторический текст Y, о котором известно только, что он рассказывает о неких событиях из эпохи (А,В), уже описанной в тексте Х, разбитом на "главы-поколения", причем порядок этих "глав" в летописи X хронологически правилен. Как узнать, какое именно поколение описано в интересующем нас тексте Y? При этом мы хотим использовать только количественные характеристики текстов, не обращаясь к их смысловому содержанию, которое может быть существенно неоднозначно и допускать различные интерпретации.

Ответ таков. Присоединим текст Y к совокупности "глав" хроники Х, считая при этом Y новой "главой" и приписав ей какой-то номер Q. Затем находим оптимальный, хронологически правильный порядок всех "глав" получившейся "летописи". При этом мы найдем правильное место и для новой "главы" Y. В простейшем случае, построив для нее график K(Q,T), можно добиться, меняя ее положение относительно других "глав", чтобы этот график был как можно ближе к идеальному. То положение, которое Y займет среди других "глав", и следует признать за искомое. Тем самым, мы датируем события, описанные в Y. Методика применима и тогда, когда рассматриваются не все имена, а только одно или несколько имен, например, какие-либо "знаменитые имена". Но в этом случае требуется дополнительный анализ, поскольку уменьшение числа используемых имен делает результаты неустойчивыми.

Метод проверен на больших текстах с большим числом имен и с заранее известной достоверной датировкой. Во всех этих случаях эффективность метода подтвердилась.

 

6. ПРИНЦИП ДУБЛИРОВАНИЯ ЧАСТОТ. МЕТОД ОБНАРУЖЕНИЯ ДУБЛИКАТОВ.

Настоящий метод является в некотором смысле частным случаем предыдущего, но ввиду важности для датировки мы выделили прием обнаружения дубликатов в отдельный раздел. Этот метод предложен А.Т.Фоменко в [884], [886], [888], [1129], [891], [895], [898], [901], [1130].

Пусть интервал времени (А,В) описан в летописи Х, разбитой на "главы-поколения" Х(Т). Пусть они в целом занумерованы хронологически верно, но среди них есть два дубликата, то есть две "главы", говорящие об одном и том же поколении, дублирующие, повторяющие друг друга. Рассмотрим простейшую ситуацию, когда одна и та же "глава" встречается в летописи Х ровно два раза, а именно, с номером Q и с номером R. Пусть Q меньше R. Наша методика позволяет обнаружить и отождествить эти дубликаты. В самом деле, ясно, что частотные графики K(Q,T) и K(R,T) имеют вид, показанный на рис.5.26.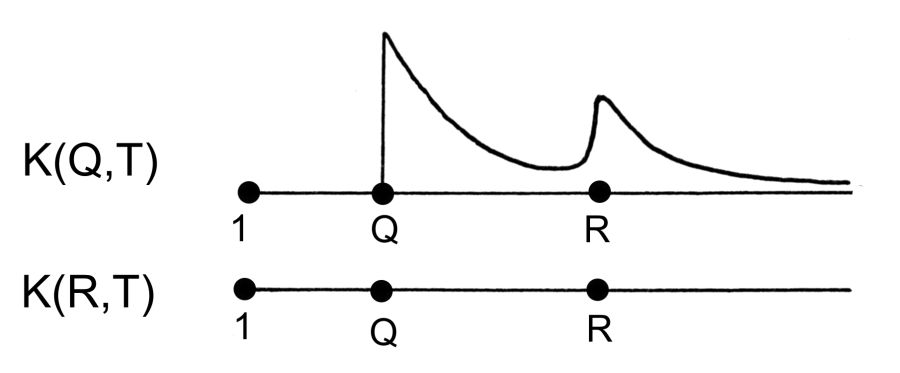

Первый график явно не удовлетворяет принципу затухания частот. Поэтому нужно переставить "главы" внутри летописи Х, чтобы добиться лучшего соответствия с теоретическим, идеальным графиком. Все числа K(R,T) равны нулю, так как в "главе" X(R) нет ни одного "нового имени" - все они уже появились в X(Q). Ясно, что наилучшее совпадение с идеальным графиком на рис.5.24 получится тогда, когда мы поместим эти два дубликата рядом или просто отождествим их.

Итак, если среди "глав" летописи, в целом занумерованных правильно, обнаружились две "главы", графики которых имеют приблизительно вид графиков на рис.5.26, то эти "главы", скорее всего, являются дубликатами. То есть, говорят примерно об одних и тех же исторических событиях, и их следует отождествить. Все сказанное переносится на случай, когда есть несколько дубликатов - три и более.

Эта методика также проверена на экспериментальном материале. В качестве одного из примеров укажем издание "Истории Флоренции" Макьявелли 1973 года (Ленинград), снабженное развернутыми комментариями. Ясно, что комментарии можно рассматривать как серию "глав", дублирующих основной текст Макьявелли. Основной текст был разбит на "главы-поколения", что позволило построить квадратную частотную матрицу К{Т}, охватывающую и комментарий к "Истории". Эта матрица имеет вид, условно показанный на рис.5.27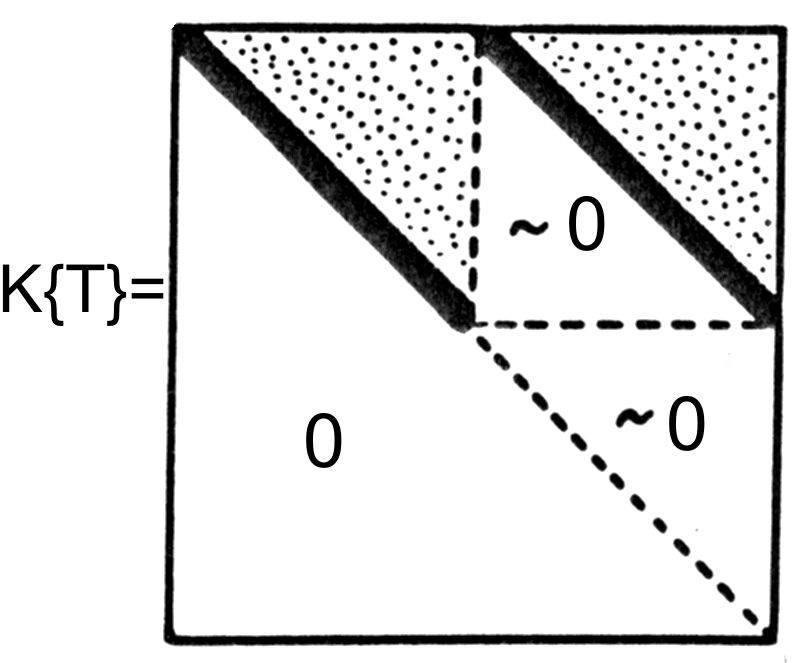, где жирные наклонные отрезки состоят из клеток, заполненных максимумами. Это означает, что наша методика успешно обнаруживает известные дубликаты. В данном случае - комментарии к основному тексту "Истории" Макьявелли.