Глава 3.
КОРРЕЛЯЦИЯ ОБЪЕМОВ ЛЕТОПИСЕЙ И ОБНАРУЖЕНИЕ ХРОНОЛОГИЧЕСКОГО СДВИГА НА 300-400 ЛЕТ В РУССКОЙ ИСТОРИИ.
2. ПРИНЦИП КОРРЕЛЯЦИИ МАКСИМУМОВ НА МАТЕРИАЛЕ ИСТОЧНИКОВ О СМУТНОМ ВРЕМЕНИ В ИСТОРИИ РОССИИ 1584-1619 ГОДОВ.
В данном разделе цитируются фрагменты работы Н.С.Келлина, Л.Е.Морозовой, А.Т.Фоменко.
(Н.С.Келлин, кандидат физико-математических наук, старший научный сотрудник Института прикладной математики им. М.В.Келдыша РАН, г.Москва.
Л.Е.Морозова, доктор исторических наук, сотрудник Института Российской Истории).
Здесь мы покажем - как принцип корреляции максимумов, сформулированный А.Т.Фоменко, проявляется на группе зависимых исторических текстов, относящихся к эпохе смутного времени на Руси конца XVI - начала XVII века н.э. Мы взяли 20 текстов, каждый из них разбили на погодные фрагменты, то есть на куски, описывающие события отдельных лет. Затем Н.С.Келлин и Л.Е.Морозова подсчитали объемы всех этих "глав". А именно, было подсчитано количество слов в каждой "главе". Полученные результаты систематизированы в виде единой таблицы 3.2, где для каждого из 20 текстов указан объем его погодных фрагментов от 1584 до 1619 годов.
Вот список исследованных текстов: 1) Повесть о честном житии, 2) Повесть како восхити, 3) Повесть како отмсти, 4) Житие Дмитрия (Тулупова), 5) Житие Дмитрия (Малютина), 6) Сказание о Гришке, 7) Сказание о Федоре, 8) Сказание о самозванце, 9) Повесть Шаховского, 10) Житие Иова, 11) Сказание Авраамия (1-я редакция), 12) Сказание Авраамия (2-я редакция), 13) Хронограф 1617 года, 14) Временник Тимофеева, 15) Повесть Катырева (1-я редакция), 16) Повесть Катырева (2-я редакция), 17) Иное сказание, 18) Пискаревский летописец, 19) Новый летописец.
Позднее были добавлены еще три текста: 20) Извет Варлаама, 21) Бельский летописец и 22) Сказание о Скопине.
Приведем таблицу 3.2 объемов погодных фрагментов для первых 19 текстов. По горизонтальной оси отложены годы, по вертикальной - номера текстов. Годы указаны сокращенно: вместо 1584, 1585, 1586 и т.д. написано просто 84, 85, 86 и так далее.
Все эти исторические тексты описывают, в основном, одни и те же события, следовательно, они зависимы, опираются на один и тот же фонд уцелевших сведений. Таблица 3.2 показывает, что имеется ярко выраженная корреляция между точками всплесков, то есть локальных максимумов функций объемов этих текстов. Видно, что почти все графики делают всплески практически одновременно, в частности, в годы: 1584, 1587, 1591, 1598.
Приведем теперь результат второго численного эксперимента, в котором к предыдущим 19 текстам были добавлены еще три текста (см. выше), а также расширены временны'е рамки. А именно, к интервалу 1584-1598 гг.н.э. присоединены годы от 1598 до 1606. Построена таблица, аналогичная предыдущей. Мы приводим таблицу 3.3, где символом Х отмечены положения локальных максимумов для всех 22 исторических текстов на интервале от 1584 года до 1606 года н.э.
Отчетливо видно, что все функции объема делают всплески практически одновременно, что объясняется зависимостью этих текстов. СЛЕДОВАТЕЛЬНО, ПРИНЦИП КОРРЕЛЯЦИИ ТОЧЕК ВСПЛЕСКОВ ФУНКЦИЙ ОБЪЕМОВ ЗАВИСИМЫХ ТЕКСТОВ ЗДЕСЬ ПОДТВЕРЖДАЕТСЯ.
Эту зависимость текстов можно выразить численно. Введем следующее "расстояние" между функциями объема vol X(t) и vol Y(t) для двух текстов X и Y, каждый из которых разбит в объединение отдельных погодных фрагментов X(t) и Y(t) соответственно. Напомним, что фрагменты X(t) и Y(t) описывают события лишь одного года t.
Пусть параметр t изменяется на отрезке времени от года A до года B. Обозначим через t(X,1), t(X,2), ... , t(X,N) - те годы, где график объемов vol X(t) делает всплески, то есть достигает локальных максимумов. Соответственно, через t(Y,1), t(Y,2), ... , t(Y,M) обозначим точки всплесков графика объемов vol Y(t).
Для каждой точки t(X,i) найдем БЛИЖАЙШУЮ К НЕЙ ТОЧКУ из последовательности t(Y,1), t(Y,2), ... , t(Y,M). Пусть это будет некоторая точка t(Y,k). Обозначим через p(i) - расстояние между ними, измеренное в годах, то есть - абсолютную величину разности t(X,i)-t(Y,k). Другими словами, выясняем - какой локальный максимум Y ближе всего расположен к выбранному локальному максимуму X.
Совершенно аналогично, меняя ролями X и Y, для каждой точки t(Y,j) найдем БЛИЖАЙШУЮ К НЕЙ ТОЧКУ из последовательности t(X,1), t(X,2), ... , t(X,N). Пусть это будет некоторая точка t(X,s). Обозначим через q(j) - расстояние между ними, измеренное в годах, то есть - абсолютную величину разности t(Y,j)-t(X,s).
Наконец, в качестве "расстояния между X и Y" мы возьмем следующую сумму: R(X,Y) = p(1)+p(2)+...+p(N)+q(1)+q(2)+...+q(M).
Смысл расстояния R(X,Y) совершенно прозрачен. Для каждого локального максимума функции vol X(t) мы находим ближайший к нему локальный максимум функции vol Y(t), определяем расстояние между ними в годах, после чего суммируем получившиеся числа. Затем повторяем ту же операцию, поменяв местами хроники X и Y. Складывая полученные числа, получаем R(X,Y). Ясно, что R(X,Y) = R(Y,X).
Если расстояние R(X,Y) равно нулю для некоторой пары текстов X и Y, следовательно, графики их функций объемов делают всплески ОДНОВРЕМЕННО. Чем больше это расстояние, тем хуже коррелируют их точки локальных максимумов. Можно рассматривать также и несимметричное расстояние от X до Y, положив p(X,Y) = p(1)+p(2)+...+p(N).
Аналогично определяется и несимметричное расстояние от Y до X, а именно, q(Y,X) = q(1)+q(2)+...+q(M).
Оценим численно степень зависимости между собой исторических текстов 1-22, перечисленных выше. Для этого подсчитаем квадратную матрицу размера 22х22 попарных расстояний R(X,Y), где X и Y независимо друг от друга пробегают все тексты 1-22. Далее подсчитаем гистограмму частот. Для этого рассмотрим горизонтальную ось, на которой отметим целые точки: 0,1,2,3,... и построим следующий график. Подсчитаем - сколько в получившейся ранее матрице {R(X,Y)} имеется нулей. Полученное число отложим по вертикали в точке с координатой 0. Затем подсчитаем - сколько в матрице {R(X,Y)} имеется единиц. Получившееся число отложим по вертикали в точке с координатой 1. И так далее. Получается график, который и называется гистограммой частот. Что можно сказать, изучая получившуюся гистограмму?
Если выбранные для анализа хроники ЗАВИСИМЫ, то большинство попарных расстояний между хрониками должно выражаться МАЛЫМИ ЧИСЛАМИ, то есть хроники должны "быть близки". Другими словами, большинство элементов матрицы {R(X,Y)} должно быть близко к нулю, <<быть мало'>>. Но в таком случае абсолютный максимум гистограммы частот должен смещаться ВЛЕВО, то есть должно быть особенно много малых частот. И напротив, если среди исследуемых текстов много НЕЗАВИСИМЫХ, то максимум гистограммы частот смещается направо, рис.3.14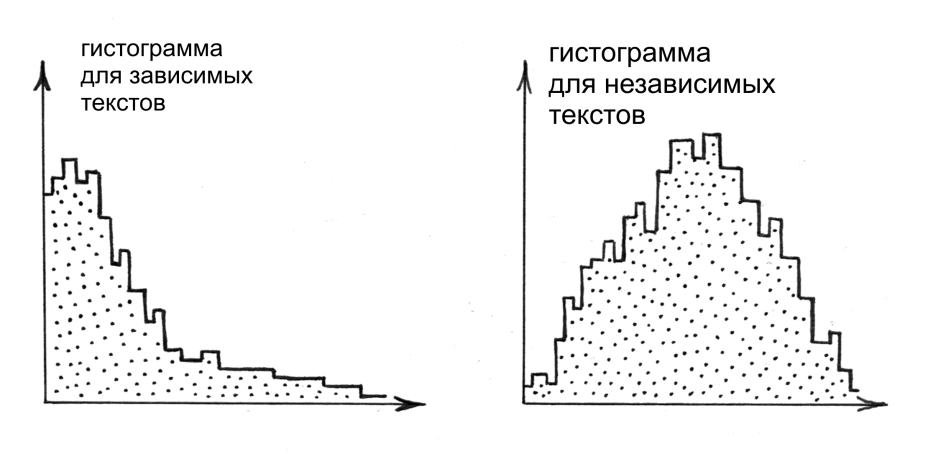
. Здесь увеличивается доля "больших" и "средних" попарных расстояний между хрониками.
Это наблюдение позволяет оценивать степень зависимости или независимости группы хроник путем построения соответствующей гистограммы частот по матрице {R(X,Y)}. А именно, смещение максимума ВЛЕВО указывает на возможную ЗАВИСИМОСТЬ хроник, а смещение максимума НАПРАВО, указывает на возможную НЕЗАВИСИМОСТЬ.
Эта идея применена для оценки степени зависимости перечисленных исторических текстов 1-22. На рис.3.15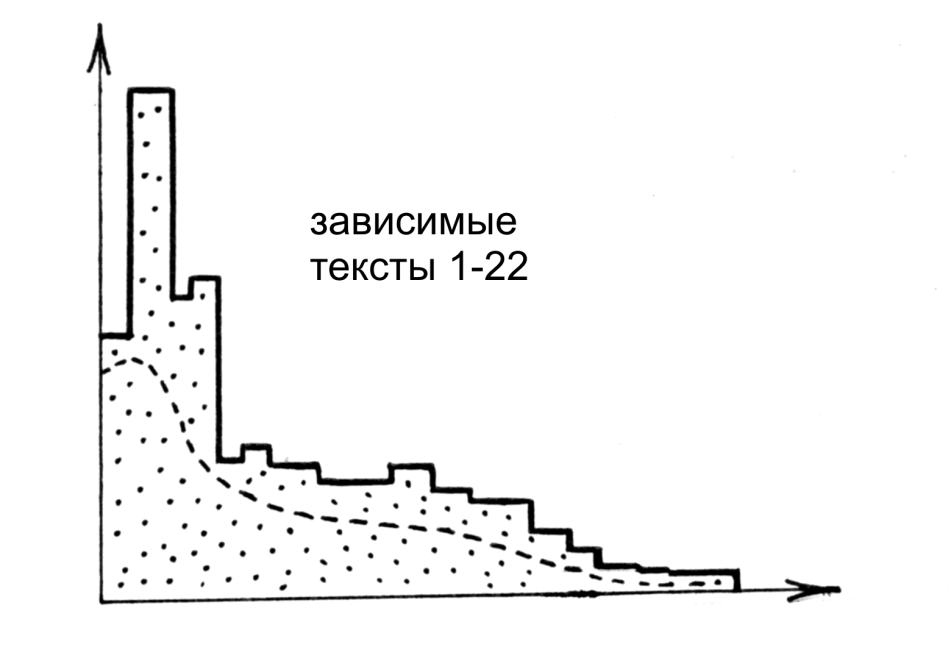
показана экспериментальная гистограмма матрицы {R(X,Y)} для текстов 1-22. В этой матрице оказалось много малых чисел, поэтому максимум гистограммы заметно смещен влево. ЭТО УКАЗЫВАЕТ НА ЗАВИСИМОСТЬ ИСТОРИЧЕСКИХ ТЕКСТОВ 1-22.
Для сравнения построим гистограмму для независимых текстов. В качестве примера мы решили сравнить указанные ниже три хроники А,В,С, с предыдущими текстами 1-22. Три дополнительные хроники таковы:
А: Повесть Временны'х Лет, якобы 850-1110 годы н.э.,
В: Академическая летопись, якобы 1336-1446 годы н.э.,
С: Никифоровская летопись, якобы 850-1430 годы н.э.
Для каждой из них вычислена функция объемов и найдены все ее локальные максимумы. Подсчитаем все попарные расстояния R(X,Y), где Х пробегает три хроники А, В, С, а Y пробегает исторические тексты 1-22. В результате получается прямоугольная матрица {R(X,Y)} размера 3х22. Далее подсчитана гистограмма частот. Результат показан на рис.3.16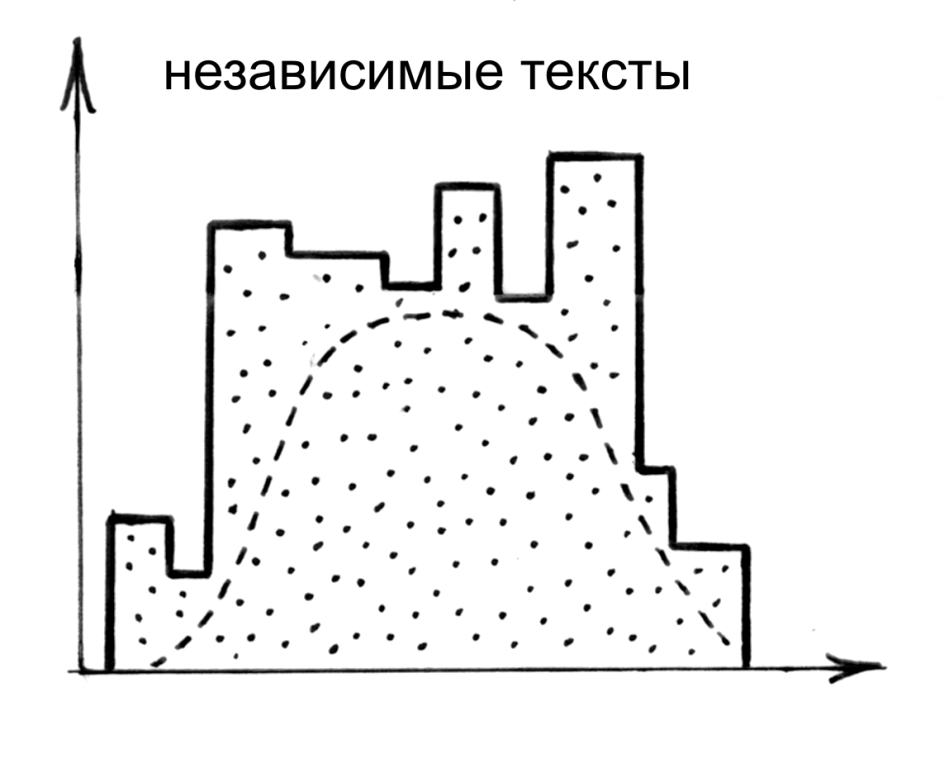
. Отчетливо виден СОВЕРШЕННО ДРУГОЙ ХАРАКТЕР гистограммы - ее максимум переместился НАПРАВО. Что указывает на НЕЗАВИСИМОСТЬ двух групп текстов: {А, В, С} и {текстов 1-22}. Конечно, внутри каждой из этих групп могут быть зависимые тексты.
Эти исследования подтвердили справедливость принципа корреляции максимумов, сформулированный А.Т.Фоменко.
