Глава 5.
АНАЛИЗ СИСТЕМАТИЧЕСКИХ ОШИБОК ЗВЕЗДНОГО КАТАЛОГА.
2. ПАРАМЕТРИЗАЦИЯ ГРУППОВЫХ И СИСТЕМАТИЧЕСКИХ ОШИБОК.
Рассмотрим некоторую совокупность звезд, например, созвездие или группу созвездий. Определим групповую ошибку в широтных координатах этих звезд как погрешность в определении широт звезд из этой совокупности, проистекающую из перемещения рассматриваемой звездной конфигурации как единого целого по сфере. Следовательно, -- и это обстоятельство мы особо подчеркнем, так как оно существенно используется в дальнейшем, -- любое подмножество этой конфигурации также перемещается по сфере как единое целое и на тот же угол, что и вся конфигурация. Такое перемещение имеет три степени свободы, то есть может быть описано тремя параметрами. Определим их.
На рис.5.1
наглядно изображена соответствующая картина. На звездной сфере с центром в точке O нанесено положение реальной эклиптики на момент времени tA. На эклиптике обозначены точки Q и R соответственно весеннего и осеннего равноденствий. Точка P отмечает северный полюс эклиптики. Точка E изображает положение некоторой звезды. Как уже говорилось, все групповые ошибки, для фиксированной группы звезд, в эклиптикальной широте, совершаемые составителем каталога, можно без ограничения общности считать следствием неправильного определения полюса эклиптики, то есть, результатом того, что вместо точки P на небесной сфере он принял в качестве полюса точку PA.
Этой точке соответствует возмущенная эклиптика, которая названа на рис.5.1 эклиптикой каталога. Ее положение можно однозначно задать следующими двумя параметрами. Во-первых, угол γ между прямыми OP и OPA, или, что то же самое, плоский угол между плоскостями реальной эклиптики и эклиптики каталога. Во-вторых, угол φ между прямой равноденствий RQ и прямой CD, образованной пересечением плоскостей реальной эклиптики и эклиптики каталога. Такая параметризация удобна для аналитических целей. Однако далее мы будем иногда наряду с φ использовать величину β, которая интерпретируется следующим образом, рис.5.1. Смещение эклиптики "разлагается" на два поворота -- вокруг оси равноденствия RQ на угол γ и вокруг оси, лежащей также в плоскости эклиптики и перпендикулярной оси RQ, на угол β. Итак, β представляет собой величину дуги QAQ, являющейся частью большого круга, проходящего через полюс PA и точку Q. Астрономический смысл точки QA весьма прозрачен. Это точка весеннего равноденствия на эклиптике каталога. Ясно, что углы γ и φ однозначно определяют углы γ и β, и наоборот. Искомую связь мы находим из сферического прямоугольного треугольника CQAQ. Здесь угол при вершине QA -- прямой, угол при вершине C равен γ, а длина дуги CQ равна β. В результате получаем:
| sinβ = sinγ · sinφ. | (5.2.1) |
Третья степень свободы заключается в повороте сферы вокруг оси PAP'A, рис.5.1. Но такой поворот меняет лишь долготы звезд и не меняет их широты. Поэтому эту степень свободы мы не рассматриваем. Отметим, что вместо указанных параметров можно выбрать любые другие базисные параметры, задающие вращение сферы. Ясно, что это не влияет на дальнейшее построение.
Посмотрим теперь, как искажаются истинные координаты звезды i при наличии такой систематической ошибки. Истинные широта BiA и долгота этой звезды LiA равны соответственно длинам дуг EE' и QE', отсчитываемым по часовой стрелке, если смотреть с полюса P. Искаженные широта и долгота bi, li равны соответственно длинам дуг EEA и QAEA. Отметим, что широты звезд, у которых истинная долгота больше долготы точки D и меньше долготы точки C, уменьшаются, а остальные -- увеличиваются, рис.5.1. Этот вывод справедлив, строго говоря, не для всех звезд. Он неверен для звезд, расположенных вблизи полюсов P и P' и находящихся на угловом расстоянии γ (или менее) от них. Однако, поскольку γ мало, звезд в такой маленькой области очень немного. Среди звезд Альмагеста их практически нет. Как мы увидим, величина γ составляет около 20'.
Учитывая малость величины γ, можно предложить следующую приближенную формулу для широтной невязки:
| Δ BiA=γ · sin(LiA+φ). | (5.2.2) |
Иначе говоря, систематическую погрешность определения широт звезд можно изобразить синусоидой, показанной на рис.5.2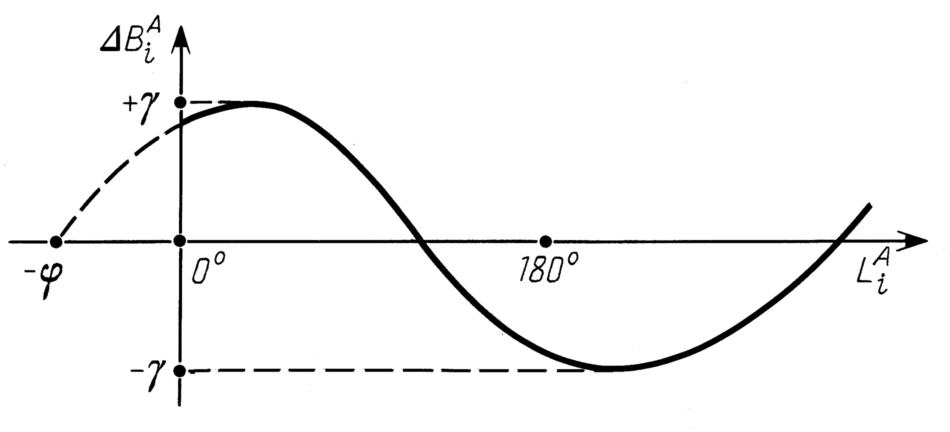
. Она очень похожа на кривую, обнаруженную ранее К.Петерсом и Е.Кнобелем [1339] при обработке каталога Альмагеста. Погрешность формулы (5.2.2) не превышает 1' для звезд, у которых |bA| ≤ 80o. Такая погрешность является для нас несущественной, и мы в дальнейшем говорить о ней не будем, считая формулу (5.2.1) абсолютно точной. Для корректности мы исключим из рассмотрения звезды, имеющие широты более 80 градусов по абсолютной величине. В дальнейшем в этой главе речь будет идти о систематической погрешности, поскольку излагаемые методы работают в предположении, что рассматривается большая совокупность звезд. Проверка того, что найденная погрешность совпадает (или не совпадает) с групповыми ошибками отдельных созвездий, представляет собой самостоятельную задачу. Применительно к Альмагесту она рассматривается ниже, в главе 6.
В предположении, что известно время tA составления каталога, можно определить параметры γ и φ, задающие систематическую ошибку, следующим образом.
1) Вычислим на момент времени tA истинные широты BiA и долготы LiA для всех звезд из рассматриваемой совокупности.
2) найдем параметры γ* и φ*, дающие решение задачи
| σ2(γ*, φ*) → min, | (5.2.3) |
где
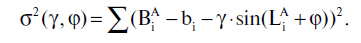
Если бы в каталоге не было других ошибок, кроме систематических, соотношение (5.2.3) превратилось бы в уравнение σ2(γ*, φ*)=0. Однако наличие случайных ошибок в координатах звезд делает минимум в (5.2.3) отличным от нуля.
В нашем случае момент tA составления каталога неизвестен. Поэтому мы вынуждены рассчитывать систематические ошибки для всех значений t из рассматриваемого интервала 0 ≤ t ≤ 25, а именно, для каждого t определяются положение реальной эклиптики и ось равноденствия. Затем, как и на рис.5.1, вводятся параметры γ=γ(t), φ=φ(t) и β=β(t), задающие взаимное положение эклиптики эпохи t и эклиптики каталога. Значения величин γ(t) и φ(t) находятся как решение задачи
Опять-таки, если бы мы имели идеальный случай и каталог не содержал бы других ошибок, кроме систематических, то соотношение (5.2.4) можно было бы, пренебрегая исключительно слабыми эффектами от собственного движения звезд, записать как уравнение σ2(γ(t), φ(t), t)=0.
По поводу эффектов от собственного движения напомним, что количество заметно движущихся звезд на небе очень мало по сравнению со всеми звездами Альмагеста. Решение последнего уравнения существовало бы при всех t, но дату tA определить из такого уравнения невозможно. Тем более ее нельзя найти из соотношения (5.2.4), заменяющего указанное уравнение в реальном случае каталога со случайными ошибками. Можно вычислить лишь систематическую ошибку как функцию предполагаемой датировки t. Эта ошибка, естественно, зависит от предполагаемой датировки -- благодаря колебанию эклиптики со временем. Именно поэтому мы здесь говорим не о датировке каталога, а о нахождении его систематической ошибки как функции предполагаемой датировки t.
В реальном каталоге, кроме указанной систематической ошибки, присутствуют и случайные ошибки. Поэтому отклонения Bi(t)-bi являются случайными величинами, значения которых разбросаны вокруг синусоиды их среднего значения, изображенной на рис.5.2. В предположении, что остальные погрешности каталога, кроме систематических, носят случайный характер, задача определения γ(t) и φ(t) является задачей определения параметров регрессии.
3. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ γ(t) И φ(t) МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ.
Найдем решение γ(t) и φ(t) задачи минимизации (5.2.4), (5.2.5). Ниже, в конкретных примерах, эта задача рассматривается для совокупностей, состоящих из различного количества звезд. Поэтому в расчетах мы будем использовать следующие нормированные величины, в которых N означает число звезд в изучаемой совокупности:
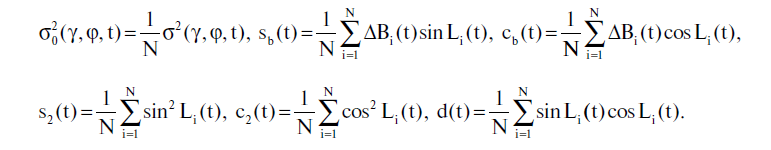
Отметим, что все эти величины могут быть вычислены для любого момента времени t, исходя из значения современных координат звезд и координат звезд в каталоге Альмагеста.
Очевидно, что задача минимизации (5.2.4) эквивалентна задаче минимизации
| σ02(γ, φ, t) → min | (5.3.1) |
в том смысле, что параметры γ(t) и φ(t), определяемые соотношением (5.3.1), совпадают с параметрами, определяемыми решением задачи (5.2.4).
Как отмечалось, решение задачи (5.3.1) имеет смысл лишь для больших совокупностей звезд, и поскольку ниже мы будем изучать статистические свойства этого решения, то здесь и далее через γstat(t) и φstat(t) обозначаются величины, удовлетворяющие соотношению (5.3.1).
Значение
| σmin(t) = σ0(γstat(t), φstat(t), t) | (5.3.2) |
имеет прозрачный физический смысл. Это среднеквадратичная широтная невязка по рассматриваемой совокупности звезд в момент времени t, получившаяся после компенсации найденной систематической ошибки γstat(t), φstat(t). Как мы увидим далее, величина σmin(t) от времени практически не зависит ввиду крайне малой скорости собственного движения подавляющего большинства звезд. Поэтому мы будем использовать также обозначение σmin. Заметим, что до компенсации этой ошибки среднеквадратичная широтная невязка в момент t равнялась величине
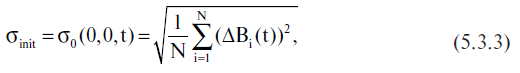
которая, вообще говоря, зависит от t. Таким образом, разность Δ σ(t) = σinit(t) - σmin(t) оценивает эффект от компенсации систематической ошибки γstat(t), φstat(t).
Далее при определении величин γstat(t) и φstat(t) из соотношения (5.3.1) момент времени t будем предполагать фиксированным. Поэтому аргумент t в выкладках мы опускаем, то есть, будем писать Li вместо Li(t),\; sb вместо sb(t) и т.д.
Для нахождения минимума в соотношении (5.3.1), возьмем частные производные функции σ02(γ, φ, t) по γ и φ и приравняем их нулю. С учетом формулы sin(Li + φ) = sin Li cos φ + cos Li sin φ, получим уравнения
| sb cos φ + cb sin φ = γ [s2 cos2 φ + 2 d cos φ sin φ + c2 sin2 φ], | (5.3.4) |
| -cb cos φ + sb sin φ = γ [-d cos2 φ + (s2 - c2) cos φ sin φ + d sin2 φ]. | (5.3.5) |
Разделив уравнение (5.3.4) на (5.3.5), получим
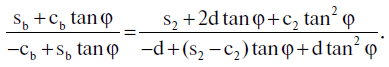
Приведя обе части этого равенства к общему знаменателю, приходим к следующему уравнению относительно tan φ:
(1+tan2 φ)(cbs2 - sbd) + (1 + tan2 φ) tan φ (cbd - sbc2) = 0.
Отсюда легко найти тангенс оптимального значения φstat:
Равенство (5.3.6) позволяет однозначно определить φstat, после чего оптимальная величина γstat может быть найдена, например, из (5.3.4):
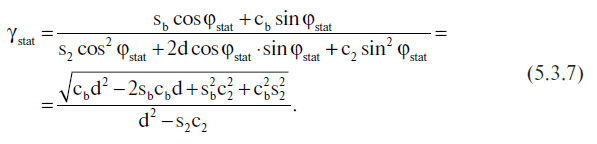
Формулы (5.3.6) и (5.3.7) дают искомое решение задачи нахождения оценок γ;stat и φ;stat методом наименьших квадратов.
Полезно провести анализ чувствительности в этой задаче. Рассмотрим частные производные второго порядка функции σ2(γ, φ, t); по γ и φ:
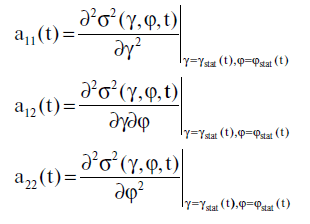
Учитывая равенства (5.3.4)--(5.3.7), нетрудно получить для этих частных производных следующие выражения:
| a11 = 2(s2 cos2 φstat + 2d cos φstat sin φstat + c2 sin2 φstat) = (2/γstat)(sb cos φstat + cb sin φstat), | |
| a12 = 2(cb cos φstat - sb sin φstat), | (5.3.8) |
| a22 = 2γ2stat(s2 sin2φstat - 2d sin φstat cos φstat + c2 cos2 φstat). |
Для оценки погрешностей в определении величины среднеквадратичной ошибки σ(γ, φ, t) при отклонении значений γ и φ от найденных оптимальных величин γstat и φstat воспользуемся следующим разложением функции σ2(γ, φ, t) в окрестности точки (γ(t), φ(t)):
| σ2(γ, φ, t) ≈ σ2min + a11(t) (γ - γstat(t))2 + 2a12(t)(γ -γstat(t))(φ - φstat(t)) + a22(t)(φ - φstat(t))2. | (5.3.9) |
В последней формуле мы пренебрегли членами третьего и более высоких порядков малости по отношению к разностям γ - γstat(t) и φ - φstat(t).
Формула (5.3.9) позволяет элементарными средствами оценить чувствительность среднеквадратичной ошибки σ(γ, φ, t) к вариациям параметров γ и φ. Для этого достаточно определить величины a11, a12 и a22, входящие в правую часть (5.3.9). После вычисления оценок γstat(t) и φstat(t) их легко найти по формуле (5.3.8).
Формула (5.3.9) показывает, что "линии уровня" среднеквадратичных ошибок являются эллипсами на плоскости (γ, φ). См.
рис.5.3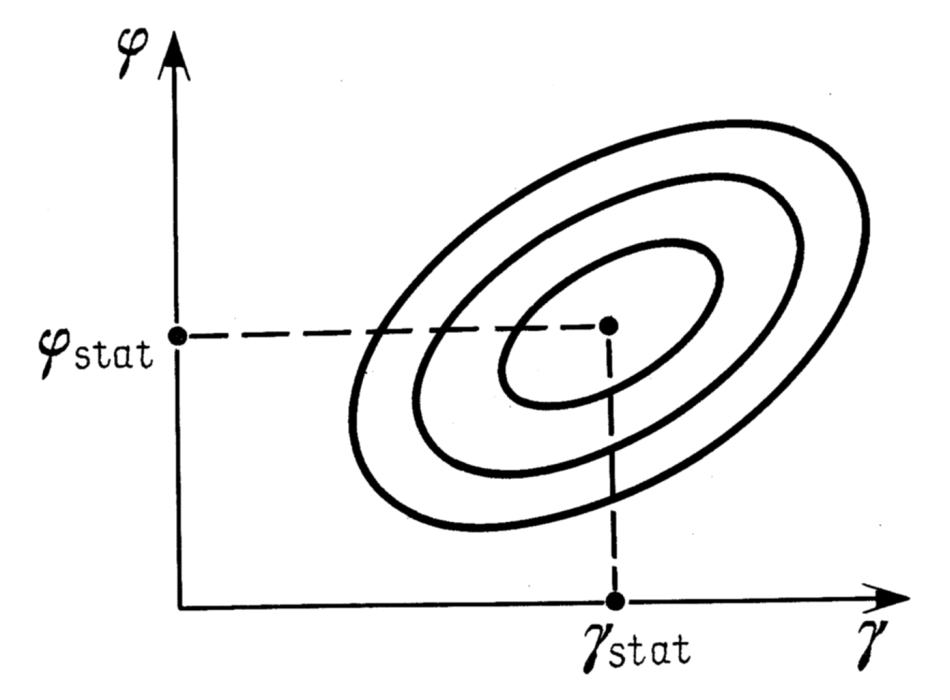
. Центром эллипса является точка (γstat, φstat), в которой значение среднеквадратичной ошибки равно σmin. Направления осей эллипсов и соотношение между ними определяются стандартными формулами аналитической геометрии через величины a11, a12, a22, а именно, угол наклона α одной из осей эллипса определяется соотношением:
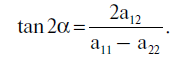
Вторая ось перпендикулярна ей. Длины осей относятся друг к другу как λ1/λ2, где λ1 и λ2 -- корни квадратного уравнения
λ2 - λ (a11 + a22) + (a11 a22 - a212) = 0.
