В.В.Калашников, Г.В.Носовский, А.Т.Фоменко
ЗВЕЗДЫ СВИДЕТЕЛЬСТВУЮТ.
Астрономический анализ хронологии.
Датировка Альмагеста Птолемея. Коперник, Тихо Браге и "античный" Гиппарх.

Том 3 , книга 1

Глава 6.
СТАТИСТИЧЕСКИЕ И ТОЧНОСТНЫЕ СВОЙСТВА КАТАЛОГА АЛЬМАГЕСТА.

3. АНАЛИЗ ОТДЕЛЬНЫХ СОЗВЕЗДИЙ АЛЬМАГЕСТА.

3.1. СОСТАВИТЕЛЬ АЛЬМАГЕСТА МОГ ДЕЛАТЬ ДЛЯ КАЖДОЙ МАЛОЙ ГРУППЫ СОЗВЕЗДИЙ СВОЮ ОШИБКУ.

Дальнейший анализ порожден следующей проблемой. Параметры γ_stat и φ_stat, определяющие систематическую ошибку, найдены по большой совокупности звезд. Они соответствуют такому повороту эклиптики, который минимизирует среднеквадратичную невязку звезд из этой совокупности. Однако нельзя априори исключать вариант, состоящий в том, что составитель делал для каждой малой совокупности звезд, например для созвездий, свою групповую ошибку. В этом случае параметры γ_stat и φ_stat представляют собой лишь некоторые усредненные значения истинных групповых ошибок и будут нам мало полезны.

Обратим внимание, что размеры доверительных интервалов для величин φ_stat, найденные в разделе 2, весьма велики. Это может объясняться как нечувствительностью широтных невязок к углу поворота φ, так и "несистематичностью" ошибки φ_stat. Иначе говоря, вероятен случай, что параметры γ_stat и φ_stat могут иметь различную природу, то есть, γ_stat является результатом ошибки, совершенной наблюдателем относительно всех звезд -- ошибки в положении эклиптики, а φ_stat -- это результат наложения и усреднения индивидуальных ошибок. Такая разница в поведении параметров легко объяснима, если рассмотреть, например, основной астрономический прибор тех времен -- армиллярную сферу, см. главу 1. В этом измерительном приборе угол между плоскостями экватора и эклиптики фиксируется раз и навсегда. Если при этом допущена ошибка, то она должна присутствовать в координатах всех звезд, которые измерены с помощью данной армиллярной сферы. Ошибка же в угле φ имеет другую природу. Она индивидуальна для каждой звезды и меняется при переходе от измерения координат одной звезды к другой.

Поэтому стоит определить групповые ошибки для отдельных созвездий Альмагеста и сравнить их с систематической ошибкой наиболее хорошо измеренной совокупности звезд Zod A.

3.2. ВЫЧИСЛЕНИЕ СИСТЕМАТИЧЕСКИХ ОШИБОК ДЛЯ ОТДЕЛЬНЫХ ГРУПП СОЗВЕЗДИЙ В АЛЬМАГЕСТЕ.

В этом разделе исследуется 21 малая совокупность звезд Альмагеста. Их перечень содержится в табл.6.5, структура которой полностью аналогична структуре табл.6.1. Дополнительно укажем лишь на принцип отбора малых звездных конфигураций. Это все зодиакальные созвездия Альмагеста, а также окружения именных звезд. Не рассматривались лишь окружения звезд Канопус и Превиндемиатрикс, -- по причинам, указанным выше, -- а также звезда Процион, из-за исключительной малочисленности звезд ее окружения.

Таблица 6.5a.

Таблица 6.5b.

Нахождение групповых ошибок для отдельных созвездий Альмагеста связано со следующими трудностями. Рассмотрим какую-либо группу звезд G и найдем для нее методом наименьших квадратов значения γ_stat^G и φ_stat^G. При этом определится минимально возможная остаточная среднеквадратичная широтная невязка σ_min^G. А также -- доля звезд p_min^G, по отношению к моменту времени t=18, имеющих остаточную широтную невязку менее 10'. Однако ввиду малочисленности отдельных групп звезд, статистическая погрешность оценок γ_stat^G и φ_stat^G слишком велика, чтобы делать на основе полученных данных достаточно обоснованные заключения.

Однако, величина σ_min^G указывает на нижнюю границу возможных среднеквадратичных ошибок в группе G. Эта минимально возможная ошибка получается при повороте системы координат на углы γ_stat^G и φ_stat^G. Разумеется, величины γ_stat^G и φ_stat^G могут сильно отличаться от γ_stat и φ_stat, полученных по большой совокупности звезд, в которую входит группа G. Критерием того, что групповая ошибка в группе G совпадает с систематической ошибкой в большой совокупности звезд, могло бы служить приблизительное равенство

σ_min^G ≈ σ₁^G, где σ₁^G -- среднеквадратичная остаточная погрешность по группе G после поворота системы координат на углы γ_stat и φ_stat. В самом деле, приведенное выше приблизительное равенство означает, что γ_stat и φ_stat -- "почти" оптимальные значения. Чтобы подкрепить этот критерий, мы определим дополнительно величины p_min^G и p₁^G -- доля звезд из G, получившая не более чем 10' широтную невязку после поворотов соответственно на (γ_stat^G,φ_stat^G) и (γ_stat,φ_stat). Если дополнительно мы увидим, что

p_min^G ≈ p₁^G, то это будет означать, что группа G действительно имеет ту же групповую ошибку, что и систематическая ошибка для большой совокупности звезд. Заметим, что последнее приблизительное соотношение не является следствием первого, а служит независимым подтверждением нашего утверждения. Заметим также, оба эти соотношения не зависят от времени, если пренебречь собственным движением звезд. Поэтому их проверка на практике может осуществляться только для одного момента времени, причем любого.

Мы рассчитали значения σ₁^G и p₁^G для различных групп G в Альмагесте для момента времени t=18. Повторим еще раз, что эти значения равны соответственно среднеквадратичной широтной невязке и доле звезд, имеющих широтную невязку не более 10' при условии, что полюс эклиптики совпадает с полюсом, определенным для наиболее хорошо измеренной совокупности звезд области Zod A. Другими словами -- при том условии, что групповые ошибки равны величинам γ_stat^{Zod A} и φ_stat^{Zod A}.

Среднеквадратичную широтную невязку и долю звезд, имеющих широтную невязку не более 10', в группе G без компенсации систематической ошибки, для t=18 мы обозначим соответственно через σ_init^G и p_init^G.

Если величина σ₁^G превышает минимально возможное значение σ_min^G незначительно, то мы вправе считать, что групповая ошибка в совокупности звезд G совпадает с систематической ошибкой в области неба Zod A. Разность величин p₁^G и p_min^G представляет собой еще один критерий близости групповой и систематической ошибок. Напомним, что величины σ_min^G и σ₁^G не зависят от времени для неподвижной совокупности звезд и слабо зависят от него для подвижных звезд. Аналогичное утверждение верно и для количества звезд, попадающих в 10-минутный интервал для широтной невязки.

Табл.6.6 содержит вычисленные нами числовые данные. Наглядно они представлены на рис.6.11 и рис.6.12. Рис.6.11 содержит информацию о величинах σ_min^G и σ₁^G, а также о p_min^G и p₁^G для всех зодиакальных созвездий Альмагеста. Они обозначены здесь Z1,..., ,Z12. На рис.6.12 представлены соответствующие результаты для окружений именных звезд Альмагеста. Они обозначены здесь S1,...,S9. Следует сказать, что для именных звезд Альмагеста, которые являются зодиакальными, их окружение не совпадает полностью с соответствующим созвездием Зодиака. Это окружение представляет собой группу звезд этого созвездия, получивших название в системе Байера. Совокупность таких звезд составляют сравнительно более яркие и, как правило, надежно отождествляемые в Альмагесте звезды. Это обстоятельство повышает надежность выводов.

Таблица 6.6a.

Таблица 6.6b.

 

3.3. ГРУППОВЫЕ ОШИБКИ ПО СОЗВЕЗДИЯМ ИЗ ХОРОШО ИЗМЕРЕННОЙ ОБЛАСТИ НЕБА В АЛЬМАГЕСТЕ ПРАКТИЧЕСКИ СОВПАДАЮТ С СИСТЕМАТИЧЕСКОЙ ОШИБКОЙ, ОБНАРУЖЕННОЙ ДЛЯ ЭТОЙ ОБЛАСТИ В ЦЕЛОМ.

Из приведенных графиков и табл.6.6 следует, что зодиакальные созвездия из части неба Zod A, -- а именно, Близнецы, Рак, Лев, Дева, Весы, Скорпион, -- обладают в Альмагесте следующим замечательным свойством. Среднеквадратичная ошибка σ₁ и доля звезд с широтной невязкой не более 10', полученные в предположении, что групповая ошибка равна (γ_stat^{Zod A}, φ_stat^{Zod A}), незначительно отличаются от величин σ_min и p_min, получаемых при оптимальном для рассматриваемого созвездия положении полюса эклиптики. Наибольшее отличие отмечено в "наиболее благополучном" созвездии Весов, где все величины σ_init, σ_min и σ₁ не превосходят 10', а p_init=p_min=p₁=83,3% . Такова доля звезд, имеющих широтную невязку не более 10'. Равенство p_init=p₁=p_min объясняется просто. Данное созвездие лежит почти на оси равноденствия и поворот γ практически не оказывает на него влияния.

Однако и для созвездий из части неба Zod B в Альмагесте сделанный вывод также может быть принят. Хотя и с б'ольшими оговорками. Впрочем, далее для нас справедливость или несправедливость этого вывода значения иметь не будет, так как в части Zod B нет ни одной именной звезды Альмагеста. Тем не менее, отметим один занятный факт, выявленный для созвездия Овна. Хотя после компенсации обнаруженной систематической ошибки, величина σ₁ понизилась по сравнению с σ_init несущественно (заметим, что и σ_min отличается от σ_init ненамного), но p₁ >> p_init=p_min, то есть помещение полюса эклиптики в найденную для Zod A точку позволило резко, до 72,7%, повысить долю хорошо измеренных в Альмагесте звезд в созвездии Овна.

Общий вывод, который вытекает из рассмотрения всех зодиакальных созвездий, следующий. Если для оптимальной величины σ_min выполнено соотношение σ_min << σ_init, то предположение о том, что групповая ошибка равна систематической, для области неба Zod A, и последующая компенсация этой ошибки ведут к соотношению σ₁ << σ_init. При этом справедливы также соотношения p₁ >> p_init, p_min >> p_init. Подобным свойством обладают в Альмагесте созвездия Близнецов, Рака, Льва, Девы, Скорпиона, Козерога, Водолея.

Если величина σ_min близка к σ_init, то, как правило, σ_min ≤ σ₁ ≤ σ_init и эффект от помещения полюса эклиптики в точку, соответствующую части неба Zod A, мало заметен. Этим свойством обладают в Альмагесте созвездия Овна (как мы отмечали, для него резко повысилась доля хорошо измеренных звезд), Тельца, Весов, Стрельца, Рыб. Среди отмеченных созвездий хорошие точностные свойства Весов, из части неба Zod A, практически не меняются при перемещении полюса эклиптики из оптимальной для него точки в точку, соответствующую области Zod A. Точностные свойства Овна в Альмагесте при этом даже улучшаются, а свойства остальных созвездий -- не меняются, оставаясь средними по качеству. Типичным примером является Телец, для которого σ_init=23,2', σ_min=18,1', σ₁=20,6', p_init=27,6%, p_min=p₁=41,4%. Из всех созвездий Альмагеста несколько выделяются Рыбы. Для них и p_min<p_init, и p₁<p_init при том, что σ_init ≈ σ_min ≈ σ₁.

 

3.4. КАК ВЛИЯЕТ КОМПЕНСАЦИЯ ОБНАРУЖЕННОЙ СИСТЕМАТИЧЕСКОЙ ОШИБКИ НА ТОЧНОСТНЫЕ СВОЙСТВА ОКРУЖЕНИЙ ИМЕННЫХ ЗВЕЗД.

Картина с окружениями именных звезд в Альмагесте более разнообразна. Прежде всего отметим окружения Аквилы и Сириуса. В обоих этих случаях компенсация обнаруженной систематической ошибки, характерной для области неба Zod A, приводит к следующему. Во-первых, - к повышению среднеквадратичной широтной невязки. В случае Сириуса - к существенному, с 15,2' до 25,9'. Во-вторых, к резкому уменьшению доли хорошо измеренных звезд. Для Аквилы -- с 40% до 13,3%, а для Сириуса -- с 47,4% до 15,8%. Это говорит о том, что групповая ошибка, совершенная составителем при измерении окружений Аквилы и Сириуса, существенно иная, чем систематическая ошибка для области неба Zod A. К сожалению, достоверно определить эти ошибки не представляется возможным. Поэтому Сириус и Аквила из дальнейшего рассмотрения были исключены.

Окружения остальных именных звезд, в общем, обладают теми же свойствами, что и зодиакальные созвездия, а именно, звезды из окружений Антареса, Аселли, Арктура, Спики, Регула существенно уменьшают среднеквадратичную ошибку, -- до значений, близких к минимально возможным, -- при компенсации групповой ошибки, равной систематической для области Zod A. При этом и доля p₁ звезд, получивших широтную невязку менее 10', существенно возрастает по сравнению с исходным значением p_init. Окружение Капеллы обладает свойством, аналогичным полученному для созвездия Овна, а именно, среднеквадратичная широтная невязка в этом окружении мало изменяется при перемещении полюса эклиптики из исходного положения в оптимальное и в положение, вычисленное для части неба Zod A. Зато в последнем из упомянутых положений резко, до 64,3%, возросла доля звезд в окружении Капеллы, "уложившихся" в 10-минутную широтную невязку. Для сравнения отметим, что в исходном положении эта доля составляла 35,7%, а в оптимальном, по среднеквадратичной широтной невязке, -- 14,3% ! Звезды из окружения Веги, напротив, получили заметное уменьшение среднеквадратичной широтной невязки. Но при перемещении полюса эклиптики в положение, характерное для области неба Zod A, произошло существенное уменьшение числа звезд с 10-минутной широтной невязкой. Таким образом, характер групповых ошибок для окружений Веги и Капеллы остается неопределенным. Это и неудивительно. Вспомним, что звезды эти находятся достаточно далеко от части неба Zod A.

 

3.5. НАЙДЕНА ЕДИНАЯ СИСТЕМАТИЧЕСКАЯ ОШИБКА, СОВЕРШЕННАЯ СОСТАВИТЕЛЕМ АЛЬМАГЕСТА В ОБЛАСТИ Zod A, И ДЛЯ БОЛЬШИНСТВА ИМЕННЫХ ЗВЕЗД.

Хотя для большей части рассматриваемых созвездий мы и обнаружили близость характеристик σ₁ и p₁ соответственно к σ_min и p_min (что говорит о систематическом характере γ_stat), вопрос о "систематичности" ошибки φ_stat остался открытым. Для его решения поступим следующим образом. Рассмотрим какое-либо созвездие Альмагеста. Ограничимся лишь зодиакальными созвездиями, где лежат, впрочем, и 6 именных звезд. Найдем для этих созвездий характеристики σ₂ и p₂, определяемые следующим образом. Первая характеристика -- это остаточная среднеквадратичная невязка. Вторая -- доля звезд из созвездия, имеющих широтную невязку не более 10'. Обе характеристики получаются при статистической ошибке γ_stat^{Zod A}, вычисленной для области Zod A, и при φ⁽²⁾, находимом из условия минимизации ошибки σ₂. Иначе говоря, для созвездия G имеем

σ₂^G = σ₂^G(t) = min_φ σ^G(γ_stat^{Zod A}, φ, t), φ⁽²⁾ = arg min_φ σ^G(γ_stat^{Zod A}, φ, t).

 

Составим табл.6.7, аналогичную табл.6.6. Более того, ряд данных в этих таблицах для наглядности повторяется. В табл.6.7 вместо величин σ₁ и p₁ занесены σ₂ и p₂. Изобразим эти данные также в виде рис.6.13, аналогичного рис.6.11. Как из таблицы, так и из рисунка видно, что компенсацией систематической ошибки γ_stat^{Zod A} в зодиакальных созвездиях из области неба Zod A и вариацией величины φ можно достичь минимально возможных значений σ₂, весьма близких к σ_min, или даже равных σ_min. При этом и величина p₂ будет близка к p_min, или равна p_min. Интересно, что такая же картина сохраняется и для созвездий из части неба Zod B.

Таблица 7.1.

Таблица 7.2.

Таблица 7.3.

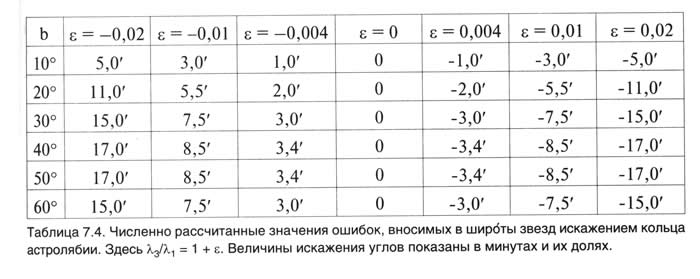
Таблица 7.4.

Все это убедительно доказывает, что найденная нами величина γ_stat^{Zod A} действительно является систематической ошибкой, совершенной составителем каталога Альмагеста при измерениях звезд из области неба Zod A, а также именных звезд. Кроме Сириуса, Аквилы и Канопуса. Величина же φ_stat^{Zod A} может быть результатом усреднения отдельных ошибок измерений, и считать ее систематической ошибкой оснований нет. Кроме того, величина φ_stat определяется достаточно грубо и в этом плане малоинформативна.

4. ВЫВОДЫ.

ВЫВОД 1. Статистически подтверждено, что полюса' эклиптики звезд из областей неба A и Zod A в Альмагесте лежат в непосредственной близости друг от друга, то есть, систематическая ошибка, совершенная составителем каталога Альмагеста в этих частях неба, одна и та же.

ВЫВОД 2. Проведенный статистический анализ не дает оснований считать, что систематические ошибки каталога Альмагеста в областях неба C, D, М, В, Zod B совпадают с ошибками для областей неба A и Zod A. При этом систематические ошибки в частях неба C, D, M с высокой вероятностью отличаются от ошибок в областях неба A и Zod A. Об ошибках в частях неба B и Zod B в Альмагесте ничего определенного сказать нельзя, так как имеющийся числовой материал не позволяет сделать уверенный статистический вывод.

ВЫВОД 3. Точность измерения звезд из областей неба A и Zod A в Альмагесте существенно выше, чем для других областей неба.

ВЫВОД 4. Среднеквадратичная остаточная широтная невязка в области неба Zod A составляет в Альмагесте 12,8'. При этом около 2/3 всех звезд из этой части неба имеют широтную невязку менее 10', то есть, укладываются по широте в заявленную Птолемеем точность каталога Альмагеста в 10 минут. Соответствующие значения для области неба A равны 16,5' и 1/2.

ВЫВОД 5. Рассмотрение зодиакальных созвездий и окружений именных звезд в Альмагесте позволяет сделать вывод, что параметр γ, - ошибка в угле наклона эклиптики, -- представляет собой систематическую ошибку. Параметр же φ может представлять собой усредненное значение групповых или индивидуальных ошибок.

ВЫВОД 6. Групповая ошибка γ в созвездиях Близнецов, Рака, Льва, Девы, Весов, Скорпиона, Стрельца, Козерога, окружениях Антареса, Аселли, Арктура, Спики, Регула близка в Альмагесте к систематической ошибке γ_stat^{Zod A}, характерной для наиболее точно измеренной части неба Zod A, или даже совпадает с ней.

ВЫВОД 7. О значении групповых ошибок в Альмагесте в созвездиях Овна и Тельца сказать ничего определенного нельзя. Они могут как совпадать с ошибками в области неба Zod A, так и отличаться от них. Ошибки в окружениях звезд Капеллы и Веги также не могут быть определены.

ВЫВОД 8. Групповые ошибки в Альмагесте в окружениях Сириуса и Аквилы отличаются от ошибки, характерной для части неба Zod A. Но найти эти ошибки нам не удалось. Групповая ошибка для созвездия Рыб, по всей вероятности, также отличается от γ_stat^{Zod A}.