Глава 8.
УГОЛ НАКЛОНА ЭКЛИПТИКИ К ЭКВАТОРУ В АЛЬМАГЕСТЕ.
1. ПРЕДСТАВЛЕНИЯ ПТОЛЕМЕЯ О ЗНАЧЕНИИ УГЛА НАКЛОНА ЭКЛИПТИКИ И СИСТЕМАТИЧЕСКАЯ ОШИБКА γ
Угол ε(t) наклона эклиптики к экватору является одной из основных астрономических величин. Знание этого угла необходимо для определения эклиптикальных координат звезд, независимо от того, как именно эти координаты определяются. Либо с помощью астролябии, как это описано в тексте Альмагеста. Либо пересчетом из экваториальных координат на специальных глобусах, как это делалось в средние века. Либо каким-либо другим способом, см. главу 2 и Введение. В настоящее время известно, что угол ε(t) меняется со временем по следующему закону:
ε(t) = 23o 27' 8,2849'' + 46,8093''t + 0,0059''t2 - 0,00183''t3, где t -- время, отсчитываемое в столетиях от 1900 года н.э. назад. См. формулу (1.5.3).
В Альмагесте подробно обсуждается способ измерения угла ε, включая описание приборов, которые при этом использовались. См. Альмагест, глава I.12 [1358]. Утверждается, что в результате этих измерений для величины 2ε получено значение, равное 11/83 полного круга, то есть в современных обозначениях εA=23o 51' 20''. Здесь через εA обозначено значение угла ε, известное автору Альмагеста.
При составлении звездного каталога Альмагеста его автор должен был пользоваться известным ему значением угла ε, фиксируя его в своем приборе. Например, в астролябии, глобусе и т.п. При этом ошибка в определении истинного значения ε, допущенная автором каталога, привела бы к повороту всей звездной сферы как целого на некоторый угол, равный величине ошибки. Другими словами, неточность, допущенная при фиксации угла ε в астрономическом приборе, приводит к систематической ошибке в координатах всех звезд каталога. Точнее, той его части, которая измерялась с помощью данного прибора. Легко понять, что систематическая ошибка такого рода влияет прежде всего на широты звезд. Именно эту систематическую ошибку мы оценивали в главе 6, определяя значения γstat(t) при различных t. Зависимость ошибки от времени t обусловлена прежде всего тем, что истинное значение угла ε(t) меняется со временем. Это изменение монотонно и практически линейно в пределах априорного интервала времени 0 ≤ t ≤ 25.
Автор звездного каталога Альмагеста, сделав в момент наблюдений ошибку в определении и фиксации угла ε в своем приборе, либо уменьшил, либо увеличил истинное значение ε. Следовательно, он либо "удревнил", либо "омолодил" свой каталог по углу наклона эклиптики к экватору. Каждая из этих возможностей могла осуществиться с вероятностью 1/2. Фактически реализовалась первая возможность, а именно, значение ε, зафиксированное в каталоге Альмагеста, равняется истинному значению ε(t) для эпохи приблизительно 1200 года до н.э. См. главу 6. Тем самым, составитель Альмагеста сильно удревнил каталог звезд.
Предположим, что каталог Альмагеста составлен в момент времени t, а его автор считал, что угол наклона эклиптики к экватору равен 23o 51' 20''. Это -- значение, указанное в Альмагесте. Допустим далее, что составитель каталога пытался зафиксировать это значение угла в своем астрономическом приборе, предназначенном для определения (путем прямых наблюдений или пересчета) эклиптикальных координат звезд. Если учесть, что при этом он совершил ошибку в пределах допуска ± Δ ε, определяемого точностью изготовления прибора, то суммарная ошибка фиксированного в приборе угла ε составляла
εA-ε(t) ± Δ ε = 23o 51' 20''- ε(t) ± Δ(ε).
Сопоставим значение этой ошибки с найденной нами выше, в главе 6, доверительной полосой γstat(t) ± Δ γ для систематической ошибки γ, а также с множеством тех γ, при которых возможно совмещение конфигурации звезд информативного ядра Альмагеста с соответствующей расчетной конфигурацией звезд, причем с гарантированной точностью 10' по широте. См. главу 7. Последнее множество непусто только при 6 ≤ t ≤ 13. См. главу 7. В качестве γstat(t) возьмем значения, определенные по части неба Zod A, поскольку, как сказано выше, часть Zod A каталога Альмагеста обладает единой систематической ошибкой γ. Доверительная полоса для γ в этой части 'уже, чем в других частях каталога, и, кроме того, все звезды информативного ядра лежат либо в самой части Zod A, либо недалеко от нее, см. главу 7.
На
рис.8.1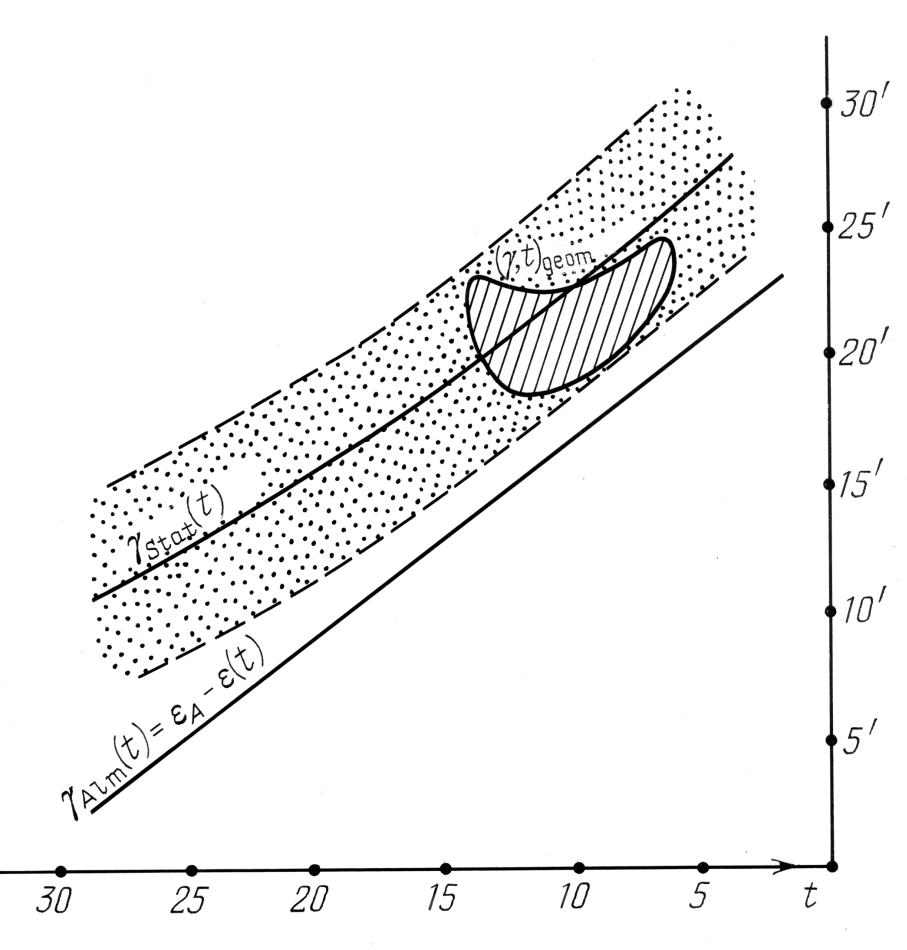
изображена доверительная полоса γstat(t) ± Δ γ, определенная по части неба Zod A с уровнем доверия 0,998. Показано также множество допустимых значений γgeom(t) для геометрической процедуры датировки, при которых максимальная широтная невязка звезд информативного ядра Альмагеста не превосходит 10'. См. главу 7. Наконец, на рис.8.1 представлен график зависимости отклонения значения ε=εA, указанного в Альмагесте, от истинного значения этого угла: γAlm (t) =εA - ε(t).
Из рис.8.1 видно, что график γAlm (t) проходит очень близко от "геометрически допустимой" области (γ, t)geom и от изображенной доверительной полосы вокруг γstat (t), хотя и не пересекает их. Чтобы это пересечение произошло, необходимо сместить график γAlm (t) приблизительно на 2,5' вверх. Тогда он начнет одновременно пересекаться и с доверительной полосой и с "геометрически допустимой" областью, которая смещена к соответствующему краю доверительной полосы. При смещении на 6,5' вверх график γAlm (t) практически совпадает с графиком γstat (t), все еще пересекаясь с "геометрически допустимой" областью. Величина необходимого смещения соответствует допуску Δ ε при фиксации εA в приборе и дает представление о той точности, с которой изготовлен астрономический прибор. В табл.8.1 приведены значения длин дуг величиной 2,5', 5', 10' и 1 градус (в мм) на астрономическом приборе, например астролябии, глобусе и т.п., радиуса 50 см, 75 см и 1 м.
Таблица 8.1.
Из табл.8.1 видно, что для ошибки Δ ε фиксации угла ε в астрономическом приборе, величина 2,5'- 5' вполне реальна для средних веков. Она соответствует допуску в линейных размерах всего 0,5--1,0 мм.
Таким образом, найденные нами значения наклона эклиптики в каталоге Альмагеста согласуются со значением εA, имеющимся в тексте Альмагеста.
