CAPITOLO 5
L’analisi degli errori sistematici dei cataloghi stellari
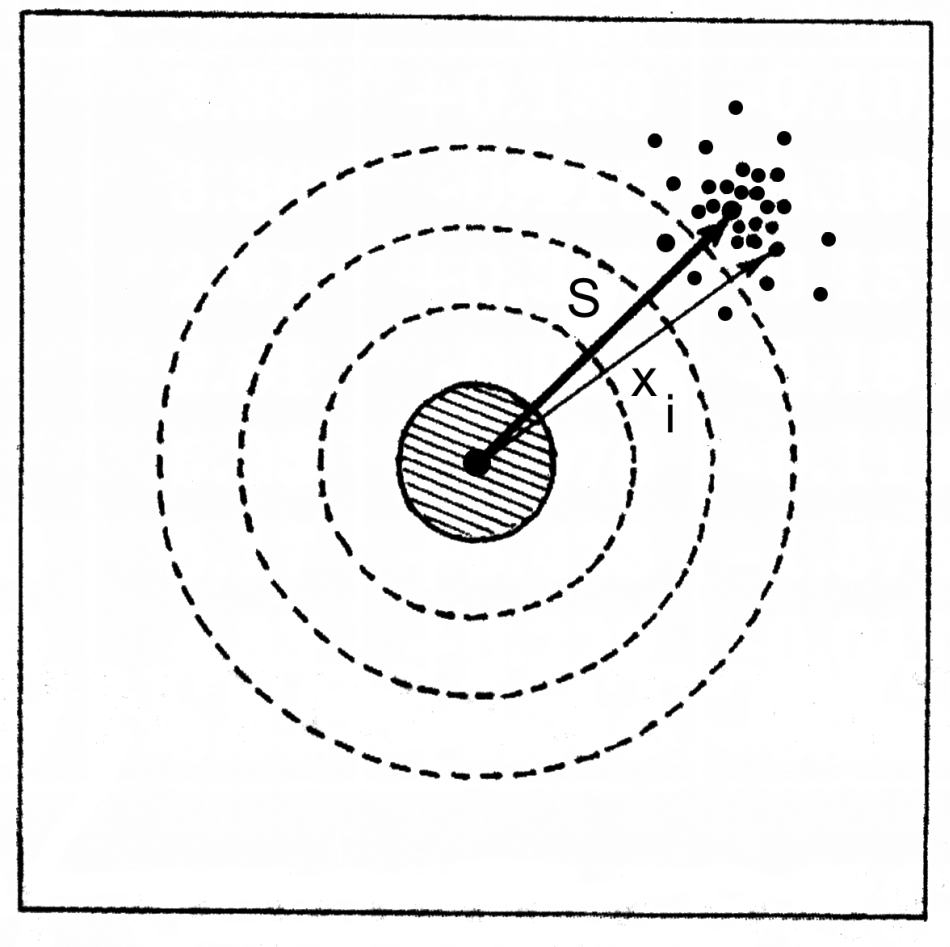
Figura 5.0.
Un bersaglio con i fori dei proiettili.
0. Concetto base.
0.1. Analogia dimostrativa.
La necessità di analizzare gli errori contenuti nei cataloghi stellari sono già stati spiegati in precedenza. Innanzitutto ci stiamo riferendo all'Almagesto; tuttavia, il metodo in questione potrà essere applicato anche ad altri cataloghi, sia quelli reali che quelli generati artificialmente. Nel presente capitolo dimostreremo come scoprire e compensare gli errori sistematici. L'idea alla base del metodo è semplice e del tutto ovvia. Inoltre, viene utilizzata in matematica statistica da ormai un po' di tempo. Al fine di spiegare il concetto di base, consideriamo il seguente esempio. Supponiamo di doverci occupare dei risultati di un concorso di tiro a segno come mostrato nella Figura 0.1.
I punti rappresentano i fori dei proiettili. Quanto è buona la precisione dei colpi? La risposta è ovvia: non lo è affatto. Tuttavia, possiamo vedere che il raggruppamento effettivo dei colpi è abbastanza buono. Questo ci porta all'assunto che il tiratore è stato in effetti bravo; il fatto che i proiettili abbiano colpito un punto che si trova a lato del bersaglio può essere spiegato da un difetto nel mirino del fucile. Ovviamente non possiamo dire nulla sulla natura del difetto senza vedere il fucile, tuttavia possiamo stimare il valore della deviazione. Un modo ragionevole per farlo ci potrebbe richiedere di determinare il centro geometrico di tutti i risultati e disegnare un vettore dal centro del bersaglio verso il centro calcolato (il vettore S sullo schema). Come facciamo a calcolare formalmente il vettore S? La procedura è semplice. Dobbiamo prendere i vettori xi che corrispondono ai risultati dei tiri e fare una media per la quantità totale dei colpi N:
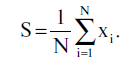
Dobbiamo anche sottolineare che il vettore S può essere calcolato in alternativa dal problema della minimizzazione della discrepanza media quadratica, per cui dobbiamo trovare il vettore S che fornisca il minimo della funzione
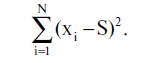
Ora stimiamo che (xi - S)2 = (xi1 - S1)2 + (xi2- S2)2, dove xi2, xi2 e S1, S2 sono le rispettive coordinate dei vettori xi e S.
La precisione effettiva del tiratore può quindi essere caratterizzata dal campo di diffusione dei risultati attorno al centro che è stato scoperto; questa precisione è quindi molto più superiore a quella di colpire il bersaglio. Il calcolo del vettore S rappresenta l'effettiva procedura di compensazione dell'errore sistematico per questo esempio (il cui valore equivale a S).
Se volessimo usare formalmente un sistema di coordinate diverso, spostando lateralmente il punto iniziale del centro del bersaglio tramite il vettore S, i risultati degli spari come indicati nel nuovo sistema di coordinate dovrebbe contenere solo le componenti casuali (quelle risultanti dal tremolio delle mani, ecc.), senza nessuna componente regolare.
Ritorniamo ora al catalogo stellare e ipotizziamo di dover verificare se potrebbe esserci un errore sistematico in alcune parti del catalogo e determinarne il valore qualora dovesse effettivamente esserci. Supponiamo di non dover ancora affrontare il problema della datazione, vale a dire che conosciamo la data di quando il catalogo tA è stato compilato per certo (ovviamente, A sta per Almagesto; comunque sia, tutte le considerazioni di cui sopra sono valide anche per gli altri cataloghi). Dobbiamo quindi confrontare le coordinate effettive delle stelle per il momento tA (noto dai cataloghi moderni precisi) con i valori delle coordinate prese dal catalogo in fase di studio, che riguardano quella parte che sarà utilizzata nella nostra ricerca. Questo confronto richiede il calcolo del tasso medio di discrepanza per le coordinate messe a confronto, proprio come abbiamo fatto nell'esempio della precisione dei colpi di fucile.
Mettiamo che il totale delle stelle nell'area selezionata sia uguale a N. Useremo le indicazioni l
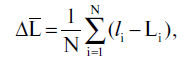
con l'errore sistematico latitudinale pari a
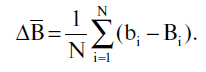
Come abbiamo già accennato, questi errori possono risultare dalla stima errata del piano dell'eclittica come anche da una serie di altre ragioni che rimangono a noi sconosciute. Non siamo in grado di dire nulla riguardo alla natura esatta di queste circostanze, tuttavia avanzeremo una serie di ipotesi. Nonostante tutto questo, possiamo e vogliamo compensare l'errore che è stato causato. Occorre solo alterare il sistema delle coordinate del catalogo analogamente a come è stato fatto nell'esempio del bersaglio, in un modo che renderebbe la media risultante dagli errori longitudinali e latitudinali pari a zero.
0.2. L’implementazione del metodo.
In questo paragrafo dimostreremo l'applicazione pratica del concetto generale di cui sopra.
Prima di tutto, vogliamo sottolineare che compenseremo solo l'errore latitudinale. Le ragioni sono state tutte citate in precedenza; in pratica ci consente di minimizzare l'errore nei calcoli, che è vitale se si considera la scarsa precisione dei vecchi cataloghi.
Pertanto, ciò che abbiamo a disposizione è il catalogo da cui abbiamo selezionato un folto gruppo di stelle il cui numero totale è pari a N, con le coordinate (li, bi)Ni=1. I loro doppioni del catalogo moderno ci sono già noti dalla procedura di identificazione condotta in precedenza. Usiamo le indicazioni (Li(t), Bi(t))Ni=1 per far riferimento alle coordinate dei menzionati doppioni calcolati per il momento t. Ora supponiamo di voler esaminare il valore del possibile errore sistematico, partendo dal presupposto che la data di compilazione del catalogo sia tA.
Definiamo
e introduciamo la discrepanza latitudinale
Il nostro obiettivo è quello di minimizzare il valore di
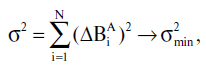
cambiando il sistema delle coordinate o disegnando semplicemente una nuova griglia di coordinate, diversa da quella utilizzata nel catalogo.
Qualora volessimo considerare il problema di minimizzare l'espressione menzionata sopra, la modifica della griglia delle coordinate potrebbe essere parametrizzata da due valori: γ e φ. Li potete vedere più avanti nella Figura 5.1. Permetteteci di spiegare cosa rappresentano. Qui, γ è l'angolo tra l'eclittica effettiva e l'eclittica del catalogo, mentre φ rappresenta l'angolo tra linea dell'equinozio e la linea di intersezione tra l'eclittica effettiva e l'eclittica del catalogo.
Per cui, dopo aver risolto il problema di minimizzare l'espressione di cui sopra, possiamo calcolare i valori di γstat e φstat che sono in grado di parametrizzare l'alterazione del sistema delle coordinate e darci il minimo iniziale. La loro forma esplicita può essere vista di seguito nelle formule 5.5.2 e 5.5.3.
Il valore di σmin è l’errore residuale della latitudine media quadratica a cui siamo arrivati dopo la compensazione dell'errore sistematico. La forma esplicita della formula di dispersione residuale σmin può essere vista di seguito, dopo la formula 5.5.10. Deriva dall'uso di γstat e φstat come parametri per l'aberrazione dell'espressione media quadratica. La derivazione di queste formule può essere vista sotto.
Tuttavia, non possiamo presumere di aver trovato l'errore sistematico (o piuttosto, i parametri γstat e φstat che lo caratterizzano) con assoluta precisione. La questione è che i singoli errori di misurazione (che sono di natura casuale) influenzano anche i valori di γstat e φstat. Pertanto, possiamo solo affermare che i valori effettivi dell'errore sistematico sono vicini a γstat e φstat.
Per rendere più precisa la nostra affermazione, introduciamo il concetto di “intervallo di confidenza”. Mettiamo che 1-ε rappresenti un certo livello di confidenza. Ad esempio, se ε = 0.1 il livello di confidenza dovrebbe essere pari a 0,9. Il livello di confidenza rappresenta la probabilità che garantisce la precisione dei nostri risultati; l'intervallo di confidenza è l'intervallo che include il valore reale sconosciuto del parametro con una probabilità minima di 1-ε. Definiamo
(ovvero l'intervallo di confidenza per il valore effettivo del parametro γ) e
che è l'intervallo di confidenza per il valore effettivo del parametro ϕ. Si può dimostrare (vedi sotto) che i valori di xε e yε possono essere calcolati dalle formule xε = qε, yε = qε, dove qε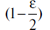 il frattile della distribuzione normale standard come calcolata dalle tabelle.
il frattile della distribuzione normale standard come calcolata dalle tabelle.
Pertanto, se volessimo definire un certo livello di confidenza 1-ε, potremmo garantire che il valore reale di γ cada nell'intervallo Iγ(ε) e che il valore di φ rientri nell'intervallo Iφ(ε), con una probabilità non inferiore a 1-ε.
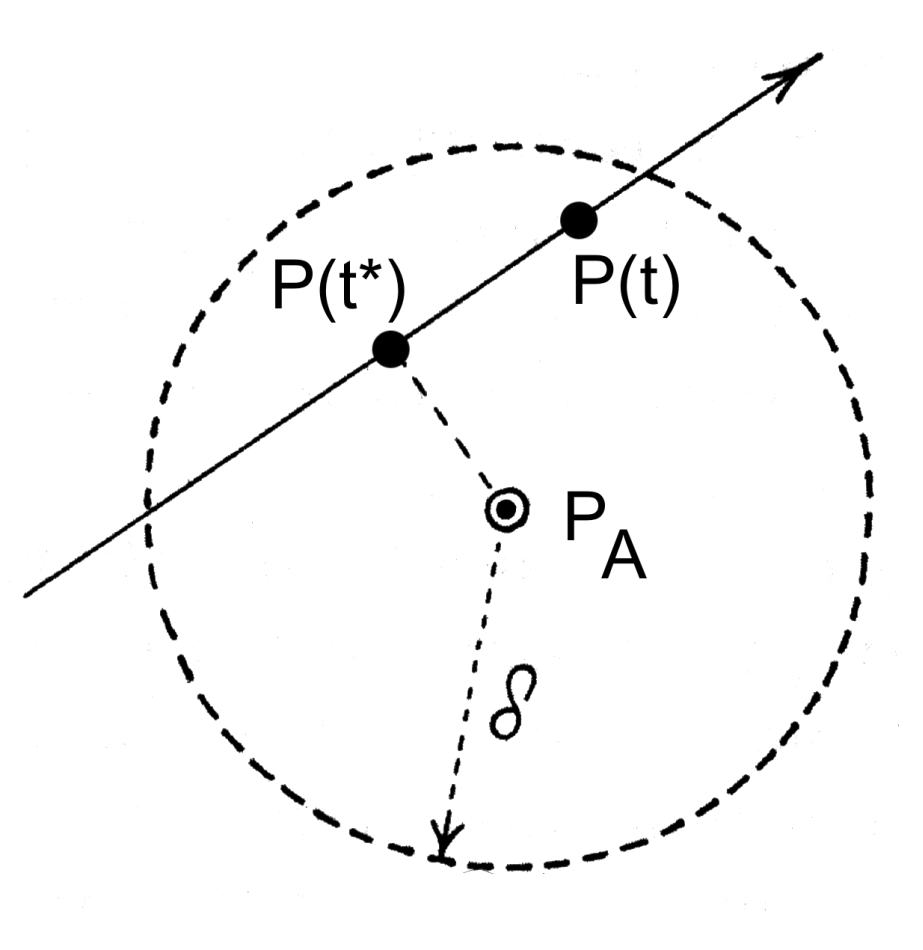
Figura 5.0a.
Un bersaglio con i fori dei proiettili.
0.3. Il valore dell’errore sistematico non può essere usato per datare il catalogo.
Ora forniamo un'interpretazione un po' diversa dei valori calcolati per γstat e φmin. L'uso delle coordinate stellari (di fatto è sufficiente considerare solo le latitudini) permette il facile calcolo dei poli dell'eclittica PA (per il catalogo in fase di studio) e P(t) per i calcoli nel catalogo del momento t, vedi il diagramma nella Figura 5.0a.
È ovvio che la distanza dell'arco tra PA e P(t) sia precisamente uguale a γstat e che la compensazione dell'errore sistematico non richieda altro che la sovrapposizione di questi due poli. Consideriamo ora i cambiamenti nel quadro generale che avvengono nel corso del tempo. Poiché P(t) si sposta all'interno dei limiti per un grado, possiamo usare un diagramma piatto e assumere che il moto di P(t) sia uniforme, vedi il diagramma nella Figura 5.0a.
La velocità v di questo moto uniforme sarebbe abbastanza facile da calcolare se conoscessimo i valori di
Pertanto, a seconda dell'errore sistematico di Tolomeo, ossia l'errore nella determinazione dell'eclittica, il momento t* potrebbe precedere la data effettiva di compilazione del catalogo o postdatarla. Nel primo caso, il catalogo (o piuttosto, la parte per la quale stiamo provando a stimare il valore di γstat), guadagnerà un'età “extra” e inizierà ad assomigliare al catalogo compilato nell'anno t*. Nel secondo caso (quando t* posdata la data effettiva della compilazione) il catalogo diventerà più recente. Di seguito potremo vedere che nell'Almagesto sono state implementate entrambe queste possibilità. Tuttavia, i termini “età extra” e “più recente” si riferiscono a un catalogo dove gli errori sistematici non sono stati compensati. Ciò che otteniamo dopo la compensazione è un “catalogo raffinato” che contiene solo gli errori casuali i cui valori medi quadratici possono essere stimati pari a σmin, sebbene non possa essere determinato nessun valore individuale.
Consideriamo ora l'uso pratico dell'idea generale come specificata nei dettagli in precedenza.
1. Definizione principale.
Da questo capitolo in poi ipotizzeremo di avere a che fare con un catalogo in cui ogni stella ha un solo doppione tra le stelle del catalogo moderno. Di conseguenza, useremo l'indice i per identificare le stelle, così come li e bi rispettivamente per la longitudine e la latitudine dell'eclittica della stella i nell'Almagesto. Li(t) e Bi(t) saranno utilizzati per riferirsi alla longitudine e latitudine effettive della stella i nell'epoca t. Tenete a mente che il tempo t è stato calcolato a ritroso dal 1900 d.C. e misurato in secoli; vale a dire che t = 3.15 corrisponde all'anno 1900 - 3.15 × 100 = 1585 d.C., ad esempio, mentre t = 22.0 corrisponde all'anno 1900 - 22 × 100 = 300 a.C.
Mettiamo che tA sia pari al periodo sconosciuto della compilazione del catalogo dell'Almagesto. La longitudine e latitudine effettive della stella i per l'anno in cui il catalogo è stato compilato, dovranno essere indicate come LiA e BiA, cioè LiA=Li(tA), BiA= Bi(tA). Mettiamo che ΔBi(t) =Bi(t) -bi rappresenti la differenza tra la latitudine effettiva della stella i per il momento t e la sua latitudine come indicata nell'Almagesto. Il valore di ΔBi(t) è stato descritto come la discrepanza latitudinale per il periodo t. Questo valore indica l'errore nella stima della latitudine della stella dell'Almagesto a condizione che sia stato compilato nell'epoca t. È ovvio che l'errore effettivo nella stima della latitudine è rappresentato da ΔBi(tA)= ΔBiA.
Come abbiamo già sottolineato nel Capitolo 3, dobbiamo solo analizzare gli errori latitudinali nel caso dell'Almagesto. Le ragioni sono state spiegate nei dettagli in precedenza.
2. La parametrizzazione degli errori di gruppo e degli errori sistematici.
Consideriamo un certo gruppo di stelle tipo una costellazione o più costellazioni. Definiremo l'errore di gruppo nelle coordinate latitudinali di queste stelle, come l'errore nella stima delle latitudini stellari per il gruppo in questione risultante dal moto della configurazione stellare sotto esame attraverso la sfera celeste nel suo insieme. Pertanto (mettiamo un'enfasi speciale su questa circostanza a causa del suo ampio utilizzo più avanti) anche ogni sottoinsieme di questa configurazione si sposterà attraverso la sfera celeste con lo stesso angolo dell'intera configurazione. Questi spostamenti hanno tre gradi di libertà, cioè possono essere descritti dalla specifica dei tre parametri che definiremo tra poco.
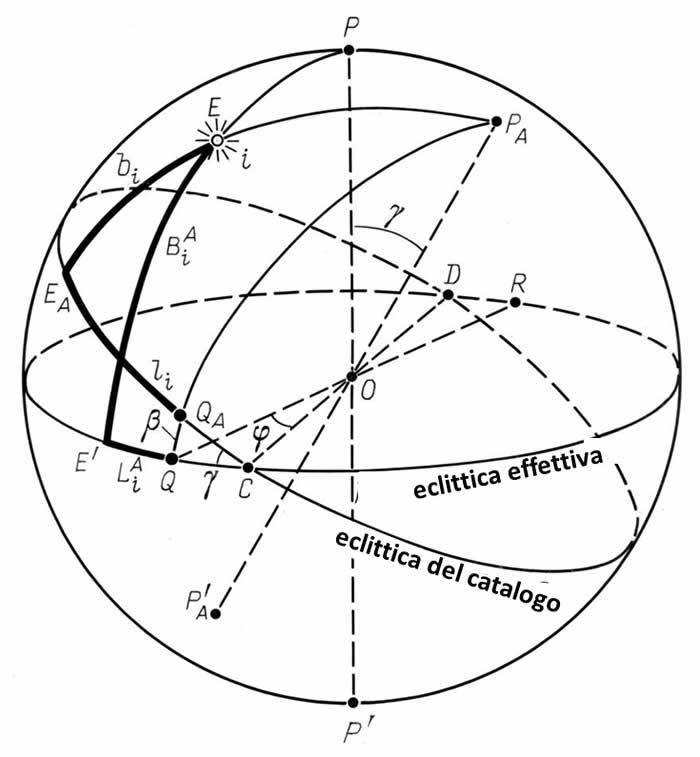
Figura 5.1.
Figura 5.1. I parametri che definiscono l’errore sistematico.
Nella Figura 5.1 si può vedere lo schema di quanto detto sopra. La posizione dell'eclittica effettiva per il momento tA, è rappresentata sulla sfera celeste il cui centro è nel punto O. I rispettivi punti dell'equinozio di primavera e di autunno sono stati segnati sull'eclittica con una Q e una R. Il punto P rappresenta il Polo Nord dell'eclittica. Il punto E rappresenta la posizione di una data stella. Come abbiamo già menzionato, tutti gli errori di gruppo per un gruppo stellare fissato nella latitudine dell'eclittica creata dal compilatore del catalogo, può essere considerato senza eccezioni come derivante dal calcolo errato del polo dell'eclittica, ovvero è risultato dal fatto che il compilatore usò un punto sbagliato come polo: PAinvece che P.
Questo punto corrisponde all'eclittica perturbata che nella Figura 5.1 viene indicata come l'eclittica del catalogo. La sua posizione può essere determinata in un solo modo dopo aver definito i seguenti due parametri: in primo luogo, l'angolo γ tra le linee OP e OPA, ossia proprio lo stesso angolo piano tra i piani dell'eclittica effettiva e l'eclittica del catalogo. In secondo luogo, dobbiamo calcolare l'angolo φ tra la linea dell'equinozio RQ e la linea CD che risulta dall'intersezione del piano dell'eclittica effettiva con quello dell'eclittica del catalogo. Questa parametrizzazione è utile per scopi analitici. Tuttavia, insieme a φ utilizzeremo anche il valore β che può essere interpretato come segue (vedere la Figura 5.1). Lo spostamento dell'eclittica può essere scomposto in due rotazioni: una attorno all'asse equinoziale RQ uguale all'angolo γ, l'altra attorno all'asse che si trova anche all'interno del piano dell'eclittica, è perpendicolare all'asse RQ ed è uguale all'angolo β. Per cui, β indica la lunghezza dell'arco QAQ che riguarda la circonferenza grande che attraversa il polo PA e il punto Q. Il significato astronomico del punto QA è abbastanza chiaro. È il punto dell'equinozio primaverile sull'eclittica del catalogo. È ovvio che gli angoli γ e φ definiscono in modo inequivocabile gli angoli γ e β; tuttavia, è vero anche il contrario. La relazione desiderata può essere determinata dalla considerazione del triangolo rettangolo sferico CQAQ. L'angolo nel vertice QA è retto, l'angolo sul vertice C è uguale a γ, mentre la lunghezza dell'arco CQ è uguale a β. Il risultato è il seguente:
sin β = sin γ · sin φ. (5.2.1)
Il terzo grado di libertà è definito dalla rotazione della sfera attorno all'asse PAP'A, vedi la Figura 5.1. Tuttavia, questa rotazione interessa solo le longitudini stellari, lasciando intatte le latitudini. Pertanto, non dovremo prendere in considerazione questo grado di libertà. Facciamo notare che al posto dei parametri specificati potremmo scegliere qualsiasi altra serie di parametri base che definiscono la rotazione della sfera. Ovviamente, questo non potrà influenzare l'ulteriore sviluppo concettuale del nostro metodo.
Ora proviamo a studiare la distorsione delle coordinate effettive della stella i influenzate da un errore sistematico di questo tipo. La latitudine effettiva e la latitudine della stella sono uguali alle lunghezze degli archi EE' e QE', contate rispettivamente in senso orario come viste dal polo P. La rispettive latitudine e longitudine distorte bi e li sono pari alle lunghezze dell'arco EEA e QAEA. Tenete presente che le latitudini delle stelle le cui longitudini effettive sono maggiori della latitudine del punto D e minori di quelle del punto C, si riducono, mentre le altre latitudini aumentano, vedi la Figura 5.1. Ad onor del vero, questo corollario non si applica a tutte le stelle. È falso per quelle situate a una distanza angolare di γ, o inferiore, dai poli P e P'. Tuttavia, poiché il valore di γ è tutt'altro che grande, ci sono pochissime stelle nelle quali si può trovare un'area così piccola. Praticamente non ce n'è nessuna nel catalogo dell'Almagesto. Come vedremo, il valore di γ equivale a circa 20'.
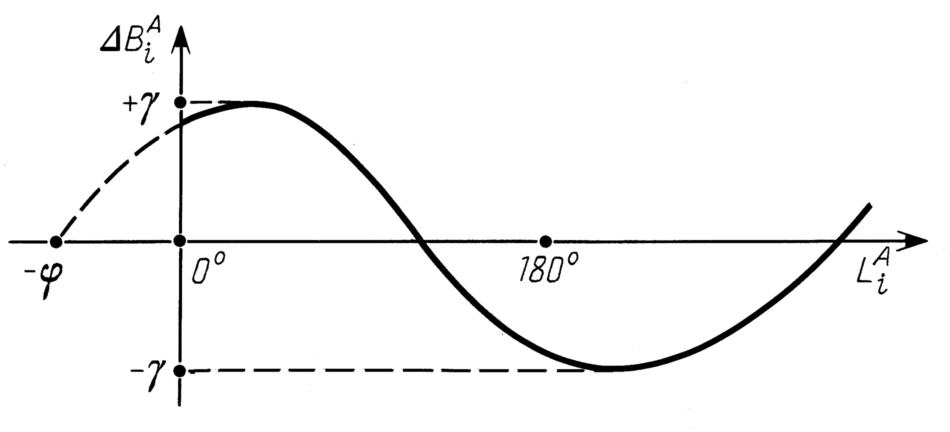
Tenendo presente che il valore di γ è piccolo, si può suggerire la seguente formula approssimativa per la discrepanza latitudinale:
Δ BiA=γ · sin(LiA+φ). (5.2.2)
In altre parole, l'errore sistematico nella stima della latitudine stellare può essere rappresentata con la sinusoide che si vede nella Figura 5.2. È molto simile alla curva scoperta in precedenza da Peters e Knobel ([1339]) mentre stavano elaborando i dati del catalogo dell'Almagesto. Il tasso di errore della formula 5.5.2 non supera 1' per le stelle il cui |bA| ≤ 80° e pertanto non ha importanza per noi. Per cui prenderemo in considerazione la formula 5.2.1 che è assolutamente precisa. Per correttezza escluderemo da ulteriori considerazioni le stelle i cui valori latitudinali assoluti superano gli 80 gradi. Faremo riferimento all'errore sistematico di seguito, poiché i metodi descritti sono validi solo partendo dal presupposto di prendere in considerazione un grande gruppo di stelle. La verifica se discrepanza rilevata coincide o meno con gli errori di gruppo per le singole costellazioni, è un problema a parte. La sua applicazione nell'Almagesto sarà considerata più avanti nel Capitolo 6.
Supponendo che il tempo tA della compilazione del catalogo sia noto, possiamo calcolare i parametri γ e φ che definiscono l'errore sistematico, come segue:
- Calcoleremo le effettive latitudini e longitudini per tutte le stelle del gruppo in esame (corrispondenti al momento tA).
- Dopodiché dobbiamo trovare i valori dei parametri γ* e φ* che ci portano alla soluzione del problema in questione.
dove
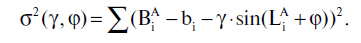
Se non ci fossero altri errori nel catalogo ad eccezione di quelli sistematici, la relazione 5.2.3 si trasformerebbe nell'equazione σ2(γ*, φ*) = 0. Tuttavia, la presenza di errori casuali nelle coordinate stellari rende il valore minimo di 5.2.3 diverso da zero.
Nella nostra situazione, il momento tA della compilazione del catalogo rimane sconosciuto; pertanto, dobbiamo calcolare gli errori sistematici per tutti i valori possibili di t nell'intervallo 0 ≤ t ≤ 25 in esame, vale a dire che la posizione dell'eclittica effettiva e l'asse dell'equinozio vengono calcolati per ogni valore di t. Quindi, proprio come si vede nella Figura 5.1, sono stati introdotti i parametri γ = γ(t), φ = φ(t) e β = β(t); definiscono le posizioni relative dell'eclittica del catalogo e dell'eclittica per l'epoca t. I valori di γ(t) e φ(t) costituiscono la soluzione del problema
dove
Ancora una volta, se questo caso fosse quello ideale (senza altre discrepanze tranne l'errore sistematico inerente al catalogo), la relazione 5.2.4 potrebbe essere trascritta con la seguente equazione (ignorando gli effetti minimi del moto proprio della stella): σ2(γ(t), φ(t), t) = 0.
Per quanto riguarda gli effetti del moto proprio, ricordiamo ai lettori che la quantità delle stelle visibilmente mobili sulla sfera celeste è molto piccola rispetto al numero totale delle stelle dell'Almagesto. La soluzione di quest'ultima equazione potrebbe esistere per tutti i valori di t; tuttavia, queste equazioni potrebbero non consentirci di calcolare la data tA. Sarebbe ancora più impossibile calcolarla dal rapporto 5.2.4 che funge da sostituito per l'equazione in questione, qualora si prendesse in considerazione un catalogo effettivo contenente degli errori casuali. Possiamo semplicemente calcolare l'errore sistematico come una funzione della presunta datazione t. Questo errore dipende naturalmente dalla presunta datazione dovuta alla fluttuazione dell'eclittica nel corso del tempo. È proprio per questo che non ci stiamo riferendo alla datazione del catalogo, ma piuttosto alla deduzione del suo errore sistematico in funzione della presunta datazione t. Il catalogo effettivo contiene degli errori casuali oltre agli errori sistematici indicati. Pertanto, le discrepanze Bi(t)-Bi sono casuali e i loro valori sono sparsi attorno alla curva sinusoidale del loro valore medio come si vede nella Figura 5.2. Supponendo che, a parte quelli sistematici, altri errori del catalogo siano di natura casuale, il problema del calcolo di γ(t) e φ(t) è quello della determinazione dei parametri di regressione.
3. Il calcolo dei parametri γ(t) e φ(t) con il metodo dei minimi quadrati.
Cerchiamo di trovare la soluzione per il problema della minimizzazione 5.2.4 e 5.2.5 espresso con γ(t) e φ(t). Negli esempi riportati qui sotto, questo problema verrà preso in considerazione per i gruppi contenenti quantità differenti di stelle. Pertanto, per i nostri calcoli utilizzeremo i seguenti valori standardizzati, nei quali N definirà la quantità di stelle nel gruppo in esame.
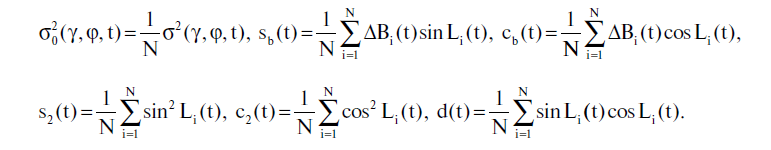
Facciamo notare che tutti questi valori possono essere calcolati per ogni momento t, a seconda dei valori delle coordinate stellari moderne e delle coordinate stellari nel catalogo dell'Almagesto.
Ovviamente, il problema di minimizzazione 5.2.4 è equivalente al problema di minimizzazione
σ02(γ, φ, t) → min (5.3.1)
nel senso che i parametri γ(t) e φ(t) definiti dalla relazione 5.3.1 coincidono con i parametri definiti dalla soluzione del problema 5.2.4.
Come abbiamo già sottolineato, la soluzione del problema 5.3.1 ha senso solo per i grandi gruppi stellari, ma dal momento che dobbiamo studiare le proprietà statistiche della seguente qui sotto, d'ora in poi utilizzeremo γstat(t) e φstat(t) per fare riferimento ai valori che soddisfano la relazione 5.3.1.
Il valore di
σmin(t) = σ0(γstat(t), φstat(t), t) (5.3.2)
è piuttosto trasparente dal punto di vista della fisica. Si tratta della discrepanza latitudinale media quadratica applicata al gruppo di stelle studiate per il momento t, risultante dalla compensazione dell'errore sistematico scoperto in γstat(t) e φstat(t). Come vedremo di seguito, il valore di σmin(t) non dipende affatto dal tempo, a causa della velocità estremamente bassa del moto proprio della maggior parte delle stelle. Pertanto utilizzeremo anche l'indicazione σmin. Tenete presente che la discrepanza latitudinale media quadratica precedente alla compensazione di questo errore sarebbe pari al seguente valore del momento t:
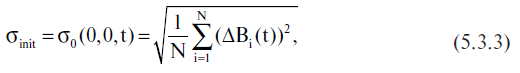
Pertanto, la differenza Δσ(t) = σiniz(t) - σmin(t) stima l'effetto di compensazione dell'errore sistematico γstat(t), φstat(t).
Più avanti, quando definiremo i valori di γstat(t) e φstat(t) dalla relazione 5.3.1, ipotizzeremo che il momento temporale t sia da fissare. Pertanto, ometteremo l'argomento t dai nostri calcoli, vale a dire che useremo Li al posto di Li(t), sb al posto di sb(t), ecc...
Per trovare il valore minimo nella relazione 5.3.1, prenderemo le derivate parziali delle funzioni da γ e φ e le faremo diventare pari a zero. Tenendo a mente la formula sin(Li + ϕ) = sinLicosφ + cosLisinφ, finiremo con le seguenti equazioni:
-cb cos φ + sb sin φ = γ [-d cos2 φ + (s2 - c2) cos φ sin φ + d sin2 φ]. (5.3.5)
Se dividessimo l’equazione 5.3.4 con la 5.3.5, otterremmo
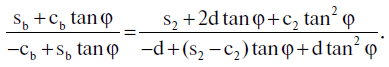
Dopo aver trasformato entrambe le parti di questa equazione in un denominatore comune, arriveremo alla seguente equazione riguardante tan φ:
Ciò semplifica il calcolo della tangente del valore ottimale di φstat:

L'equazione 5.3.6 consente una determinazione unica di φstat; dopodiché, il valore ottimale di γstat potrà essere dedotto dalla 5.3.4, ad esempio:
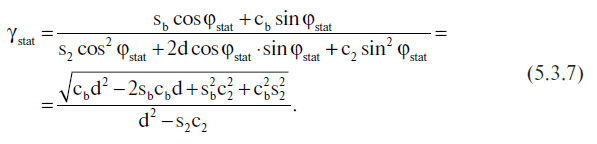
Le formule 5.3.6 e 5.3.7 rendono possibile la ricerca della soluzione desiderata per il problema del calcolo delle stime per φstat e γstat con il metodo dei minimi quadrati.
Sarebbe opportuno condurre un'analisi sensibile a questo problema. Consideriamo il secondo ordine delle derivate parziali della funzione σ2(γ, φ, t) rispetto a γ e φ:γstat
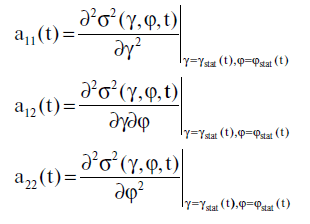
Tenendo a mente le equazioni 5.3.4-5.3.7 possiamo facilmente determinare le seguenti espressioni per queste derivate parziali:
| a11 = 2(s2 cos2 φstat + 2d cos φstat sin φstat + c2 sin2 φstat) = (2/γstat)(sb cos φstat + cb sin φstat), | |
| a12 = 2(cb cos φstat - sb sin φstat), | (5.3.8) |
| a22 = 2γ2stat(s2 sin2φstat - 2d sin φstat cos φstat + c2 cos2 φstat). |
Per poter stimare gli errori nel calcolo del tasso dell'errore medio quadratico σ(γ, φ, t) considerando l'aberrazione dei valori γ e φ rispetto al valori ottimali calcolati φstat e γstat, utilizziamo la seguente decomposizione della funzione σ2(γ, φ, t) per la vicinanza del punto (γ(t), φ(t)):
Per poter stimare gli errori nel calcolo del tasso dell'errore medio quadratico σ(γ, φ, t) considerando l'aberrazione dei valori γ e φ rispetto al valori ottimali calcolati φstat e γstat, utilizziamo la seguente decomposizione della funzione σ2(γ, φ, t) per la vicinanza del punto (γ(t), φ(t)):
Nell'ultima formula abbiamo ignorato i termini di magnitudine pari e superiori a tre, come riferito per le differenze γ - γstat(t) e φ - φstat(t).
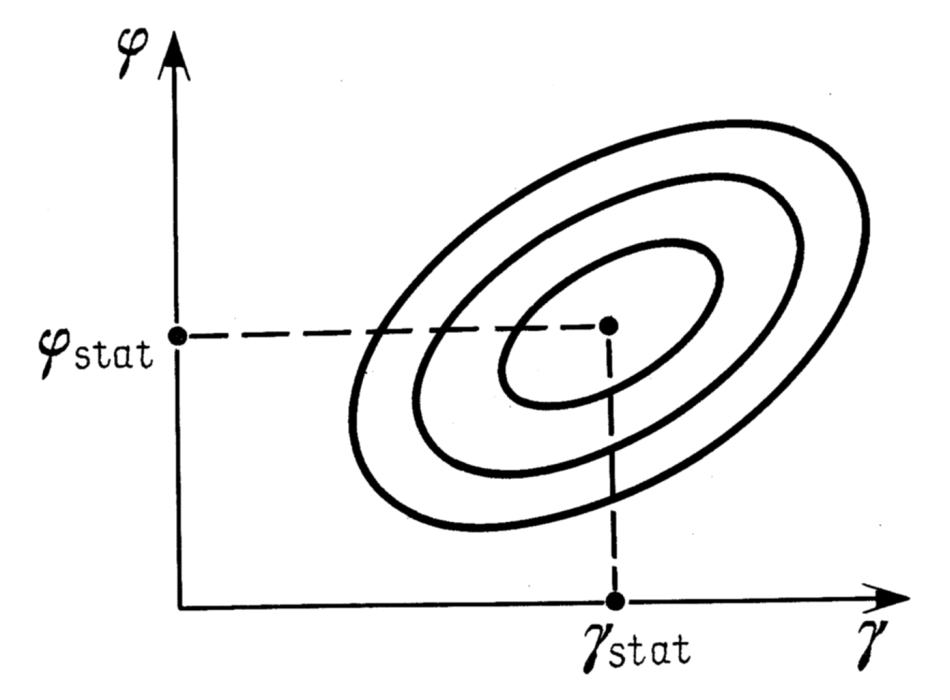
Figura 5.3.
Le curve di livello dell'errore medio quadratico σ(γ, φ, t), dove t è un valore fisso.
La formula (5.3.9) consente una stima elementare della sensibilità dell'errore medio quadratico σ(γ, φ, t) per la variazione dei parametri γ e φ. Per questo scopo è sufficiente determinare i valoria11, a12 e a22 pertinenti alla parte corretta di 5.3.9, che dopo la stima di γstat(t) e φstat(t) possono essere facilmente calcolati con φstatla formula 5.3.8.
La formula 5.3.9 dimostra che le “curve di livello” degli errori medi quadratici si manifestano come delle ellissi sul piano (γ, φ), vedi la Figura 5.3. Il centro delle ellissi è nel punto (γstat, φstat) per il quale il valore dell'errore medio quadratico è uguale a σmin. La direzione degli assi dell'ellittica e la relazione tra loro sono determinate dalle formule standard di geometria analitica attraverso i valori a11, a12 e a22, vale a dire che l'angolo di inclinazione α di uno degli assi de'ellisse è determinato dalla seguente relazione:
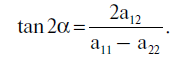
Il secondo asse è perpendicolare al primo. Le lunghezze degli assi si relazionano l'una all'altra con λ1/λ2, dove λ1 и λ2sono le radici dell'equazione quadratica