CAPITOLO 7
La datazione del catalogo stellare dell’Almagesto. Il metodo statistico e quello geometrico.
8. La datazione geometrica dell’Almagesto. L’influenza degli errori dei vari strumenti astronomici sul risultato della datazione.
8.1. Gli strumenti astronomici fabbricati male potrebbero aver compromesso la precisione delle misurazioni.
Il metodo di datazione geometrica non contiene il fattore di probabilità ε. Tuttavia bisogna testare la sua stabilità rispetto alla precisione dichiarata nel catalogo, così come il contingente del kernel informativo. Le conclusioni a cui siamo giunti sono in buona parte simili a quelli del paragrafo 6. Per cui, aumentando il livello di precisione da 10' a 15' si sposta il limite inferiore dell'intervallo di datazione indietro al 250 d.C. Anche l'intervallo di datazione del kernel informativo compatto delle 6 stelle che si trovano nell'area Zod A o nelle sue immediate vicinanze, è cresciuto solo di 100 anni, diventando quindi il 500 d.C. - 1300 d.C. Una volta tolta la stella veloce Arturo dal kernel informativo del catalogo, l'intervallo di datazione si espande e diventa il 200 d.C. - 1600 d.C.
Pertanto, l'intervallo di datazione del catalogo dell'Almagesto stimato per mezzo di una procedura geometrica, non riesce a coprire l'epoca scaligeriana di Tolomeo, figuriamoci quella di Ipparco.
A parte questo, dimostreremo la stabilità della procedura di datazione geometrica con la possibile influenza degli errori causati dagli strumenti astronomici.
Il metodo di datazione geometrica si basa sugli errori dell'osservatore durante la stima del polo dell'eclittica. Devono essere prese in considerazione tutte le possibili rotazioni della sfera, in altre parole la rotazione ortogonale della griglia delle coordinate nello spazio. Se fossimo interessati solo alle latitudini, la rotazione della sfera potrebbe essere definita esclusivamente dal vettore di spostamento del polo, poiché il componente residuale di rotazione non influisce sulle latitudini.
Supponiamo che il vettore di spostamento dei poli abbia le coordinate (γ, φ). Se riuscissimo a far ruotare la sfera in modo tale da ridurre la discrepanza latitudinale massima (per esempio quella del kernel informativo del catalogo, ossia le stelle zodiacali in esso contenute) a un valore inferiore a quello di Δ, la datazione del catalogo sarebbe fattibile. Ricordiamo ai lettori che per il catalogo dell'Almagesto Δ = 10'.
In tutti i casi considerati sopra, le rotazioni ortogonali della sfera celeste erano sufficienti ad abbassare la discrepanza latitudinale massima sotto il tasso di precisione dichiarato del catalogo Δ, datando ipso facto il catalogo e confermando anche la precisione di Δ dichiarata da Tolomeo. Tuttavia, finora non abbiamo escluso il fatto che Tolomeo potesse aver usato uno strumento astronomico imperfetto. Per esempio, un astrolabio provvisto di anelli metallici con una leggera aberrazione nella perfezione della forma circolare. Un anello che potrebbe essere oblato da un'estremità e allungato dall'altra. A parte questo, alcuni piani di questi strumenti, nella realtà potrebbero non essere perpendicolari come avrebbero dovuto essere idealmente. Alcuni angoli potrebbero essere distorti e dare delle misure leggermente diverse su assi differenti.
In altre parole, sia lo strumento che la griglia delle coordinate che definisce lo spazio tridimensionale, potrebbe essere soggetta a una certa deformazione. Potrebbe persino far sballare del tutto i risultati della misurazione. E' del tutto logico chiedersi come mai delle lievi deformazioni dello strumento o la griglia delle coordinate a cui corrisponde detto strumento, possano influenzare il risultato della misurazione. Quanto grandi dovrebbero essere le distorsioni dello strumento, per compromettere sostanzialmente i risultati delle osservazioni? Rispondiamo a tutte queste domande di seguito.
8.2. La formulazione matematica del problema.
Formuliamo il problema con precisi termini matematici. Consideriamo uno spazio tridimensionale euclideo il cui centro contenga una sfera che corrisponde alle tre coordinate reciprocamente ortogonali agli assi. Questi assi definiscono le coppie dei piani delle coordinate ortogonali. Per poter misurare le coordinate stellari dell'eclittica, si dovrebbe proiettare la stella dall'inizio della scala delle coordinate al punto A, vedere la Figura. 7.32. Il punto A risultante sulla sfera viene definito dalle sue coordinate sferiche, per esempio. Dopodiché, queste coordinate vengono incluse nel catalogo dell'osservatore.
Consideriamo ora l'asse z da indirizzare al polo P dell'eclittica, mentre il piano xy attraversa l'eclittica della sfera. Abbiamo già spiegato nei dettagli il fatto che le latitudini stellari sono le coordinate misurate in modo molto affidabile. Pertanto, quella che di più interessa a noi è la latitudine della stella A. La latitudine viene misurata attraverso il meridiano che collega il polo P dell'eclittica alla stella A. La latitudine zero è l'eclittica stessa, ossia il parallelo zero. Nella Figura 7.32 la latitudine dell'eclittica della stella A è stata misurata dalla lunghezza dell'arco AB.
Il processo di inclusione delle coordinate stellari sopra descritto, implica che lo strumento dell'osservatore crei un sistema ideale di coordinate sferiche nello spazio tridimensionale circostante. Tuttavia, lo strumento effettivo potrebbe essere leggermente deformato. Ignorando gli effetti di secondo ordine e senza una qualsiasi perdita di generalità, si potrebbe considerare che la deformazione dello strumento abbia causato una sorta di trasformazione dello spazio lineare nel sistema euclideo delle coordinate. Sarebbe ovvio considerare questa trasformazione lineare come un caso identico, dal momento che una grande distorsione verrebbe notata da un osservatore che rivendica una precisione di 10'. Anche se la deformazione del sistema delle coordinate contenesse delle piccole perturbazioni non lineari, staremmo di fatto considerando la prima approssimazione lineare che descrive la distorsione dello strumento.
Una trasformazione lineare dello spazio tridimensionale che lascia intatto l'inizio delle coordinate, è specificata dalla matrice

Questa trasformazione distorce il sistema euclideo delle coordinate originale. La teoria elementare della forma quadratica ci dice esplicitamente che una trasformazione lineare non degenerata vicina a quella identica deforma la sfera creando una specie di ellissoide, vedere la Figura 7.33. Per cui, sebbene le rette originali delle coordinate ortogonali vengono in qualche modo spostate, cessando così di essere ortogonali, si possono sempre trovare tre nuove rette ortogonali allineate lungo gli assi ellissoidali. Nella Figura 7.33, queste tre nuove rette sono state indicate con x', y' e z'.
Pertanto, i fini della nostra ricerca ci consentono di ipotizzare che la trasformazione lineare deforma la sfera nella seguente maniera: la prima cosa che succede è una specie di rotazione (la trasformazione ortogonale) che trasforma gli assi ortogonali x, y e z nei nuovi assi ortogonali x', y' e z'. Quest'ultima trasformazione è stata specificata in modo univoco dalla matrice diagonale

I coefficienti di allungamento λ1, λ2 e λ3 rappresentano alcuni numeri reali che possono essere positivi o negativi, ma il concetto stesso del problema implica che siano differenti da zero.
8.3. La deformazione della sfera in un ellissoide.
Le deformazioni della griglia delle coordinate che sono state causate dalle curve ortogonali, sono state studiate in precedenza, per cui ora possiamo concentrare tutta la nostra attenzione sulla seconda trasformazione, vale a dire quella della similarità definita dalla matrice diagonale R.
Pertanto, senza perdita di generalità possiamo ipotizzare che la deformazione dello strumento astronomico che genera una trasformazione lineare nella griglia delle coordinate euclidee tridimensionali, è specificato dalla trasformazione della similarità R con i coefficienti di allungamento λ1, λ2 e λ3, vedere la Figura 7.34. Facciamo notare che i valori di λi possono essere pari a uno, maggiori di uno o più piccoli di uno, a prescindere l'uno dall'altro. Pertanto, quando ci riferiamo ai coefficienti di allungamento, in realtà non si tratta solo di questo (l'espansione dimensionale lineare lungo l'asse), ma anche della possibile compressione o riduzione dimensionale lineare. Se λi fosse maggiore di 1 per alcuni punti di i, avremmo l'espansione; se il valore fosse inferiore a uno, potremmo osservare che sull'asse in questione avviene la compressione.

Figura 7.32. La procedura geometrica di
datazione del catalogo dell'Almagesto.
Figura 7.33.
Le discrepanze latitudinali individuali del catalogo
dell’Almagesto con β ≈ 0’ ≈ 21’.
I valori di λ1, λ2 e λ3 possono essere considerati come i valori del semiasse dell'ellissoide. Nella Figura 7.34 questi semi-assi sono rappresentati con i segmenti Oλ1,Oλ2 e Oλ3.
8.4. Le discrepanze delle misurazioni nel “sistema delle coordinate ellissoidali”.
Procediamo a discutere i cambiamenti nel sistema delle coordinate deformate descritte sopra, quello che chiameremo “ellissoidale”. Nella Figura. 7.35 il piano del disegno attraversa il centro O, la stella A e il polo P dell'eclittica. Questo piano interseca l'ellissoide creato dallo strumento lungo l'ellisse, che è stato disegnato nella Figura 7.35 con una curva continua. La rispettiva circonferenza dello strumento ideale è stata disegnata con una curva tratteggiata. Dal momento che siamo solo interessati alle latitudini, ricordiamo ai lettori che sono quelle che vengono comunemente più contate dal punto dell'eclittica, ossia il punto M della Figura 7.35 utilizzato come punto di riferimento. L'osservatore ha diviso l'arco MP' in 90 parti uguali, per cui ha diviso l'anello (o ellisse) in gradi. Dal momento che quella che abbiamo diviso era un'ellisse e non un cerchio, i gradi uniformi sull'ellisse distorcono di qualche misura gli angoli, per cui la divisione non sarà uniforme. Ipotizziamo che l'osservatore non l'abbia notato, altrimenti lo strumento sarebbe stato messo a punto.
Dopo l'osservazione, la posizione della stella effettiva A è stata contrassegnata dallo “strumento ellittico” con A'. L'osservatore l'ha considerata come la latitudine effettiva della stella e l'ha inserita nel suo catalogo, in cui ovviamente si presume che il sistema delle coordinate sia idealmente sferico; pertanto è stata trascritta come un certo punto A". La posizione effettiva della stella si sarebbe spostata e abbassata un po', se 1 = λ1> λ3.
La natura dell'ellisse dovrebbe indicare il punto P' sopra il punto P (in altre parola con 1 = λ1 < λ3), per cui la stella verrà spostata in una direzione diversa. In questo caso il punto A" sarà maggiore del punto A sulla circonferenza PM. Ovviamente, la risultante trasformazione della circonferenza (da A ad A") è di natura non lineare. Può essere continua fino alla trasformazione dell'intero piano e dell'intero spazio tridimensionale. Il punto di riferimento iniziale delle coordinate rimane lo stesso tutto il tempo. Tuttavia, poiché consideriamo che l'effetto di distorsione dello strumento sia stato lieve, basterà studiare l'approssimazione lineare come detto in precedenza. In altre parole, se utilizzassimo la parte principale lineare al posto dell'intera trasformazione non lineare descritta sopra, avremmo un errore non troppo grande. Questa parte principale si manifesta nell'allungamento dei tre assi ortogonali con i coefficienti λ1, λ2 e λ3.
Per cui, siamo tornati alla formulazione matematica del problema riportata sopra (vedere i paragrafi 8.2 e 8.3). I valori precisi degli errori introdotti nelle latitudini stellari da questa trasformazione sono stati calcolati dagli autori; i risultati dei calcoli sono stati riportati nella Tabella 7.4.
Tabella 7.4. I valori dell'errore calcolati quantitativamente, inerenti alle latitudini stellari e risultanti dalle imperfezioni nella forma degli anelli dell'astrolabio. Qui, λ3 / λ1 = 1 + ε. I valori della distorsione angolare sono indicati in minuti e frazioni di minuti. |
|||||||
| b | ε = | ||||||
| -0.02 | -0.01 | -0.004 | 0 | 0.004 | 0.01 | 0.02 | |
| 10° | 5.0’ | 3.0’ | 1.0’ | 0 | -1.0’ | -3.0’ | -5.0’ |
| 20° | 11.0’ | 5.5’ | 2.0’ | 0 | -2.0’ | -5.5’ | -11.0’ |
| 30° | 15.0’ | 7.5’ | 3.0’ | 0 | -3.0’ | -7.5’ | -15.0’ |
| 40° | 17.0’ | 8.5’ | 3.4’ | 0 | -3.4’ | -8.5’ | -17.0’ |
| 50° | 17.0’ | 8.5’ | 3.4’ | 0 | -3.4’ | -8.5’ | -17.0’ |
| 60° | 15.0’ | 7.5’ | 3.0’ | 0 | -3.0’ | -7.5’ | -15.0’ |
8.5. La stima della distorsione degli angoli misurata dallo “strumento marginalmente ellissoidale”.
Pertanto, prendiamo in considerazione la trasformazione lineare dello spazio tridimensionale definito dai tre valori λ1, λ2 e λ3, ossia la matrice

Dobbiamo stimare la risultante distorsione dell'angolo. Mettiamo che ψ sia uguale alla latitudine effettiva della stella effettiva. Se venisse misurata con uno strumento ellissoidale, si trasformerebbe nel valore diverso ψ'. La differenza Δψ = ψ - ψ' è il valore della distorsione effettiva. Geometricamente, la distorsione è specificata dall'angolo Δψ tra la direzione della stella effettiva e la direzione misurata per mezzo di uno strumento deformato.
Secondo noi non è necessario considerare l'intero spazio tridimensionale, ma che dopo tutto dovrebbe essere sufficiente il piano piatto. Infatti, la Figura 7.36 dimostra che la trasformazione lineare R sposta la stella A nella nuova posizione A", mentre la parallela della stella A si trasformerà nella parallela della stella A". Questo è il risultato del piano ortogonale all'asse OP, che definisce la parallela della stella A, la quale occuperà una nuova posizione e resterà ortogonale all'asse OP. Dal momento che siamo interessati solo alle latitudini, sarà sufficiente studiare il punto B al posto del punto A", quello che si trova sul meridiano della stella A, vedere la Figura 7.36.
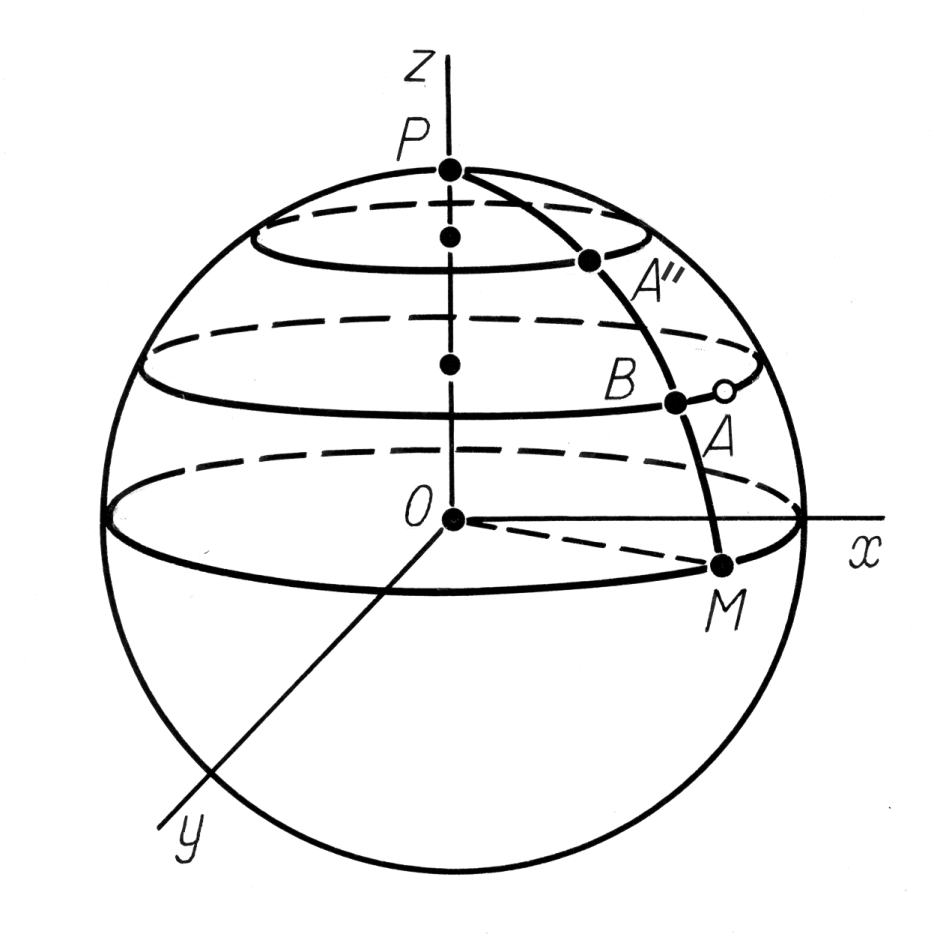
Figura 7.36.
Come conseguenza della trasformazione lineare del sistema
delle coordinate, la stella dovrà “alterare la sua posizione”
(qui λ1 = 1).
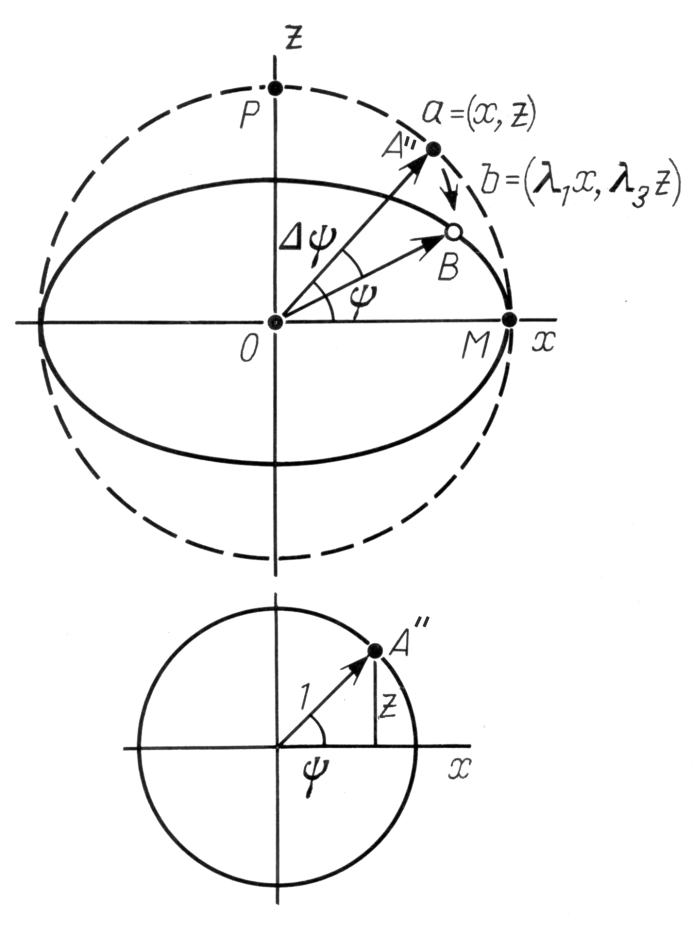
Figura 7.37.
La trasformazione di una circonferenza in un ellisse
a seguito di una lieve distorsione del sistema delle coordinate.
La trasformazione R fa in modo che il piano che attraversa l'asse OP e il meridiano della stella A ruotino attorno all'asse OP. Il piano spostato genera una trasformazione lineare della similarità; il problema tridimensionale diventa così bidimensionale, per cui dovremo studiare l'ellisse nelle due dimensioni, vedere la Figura 7.37. Ignorando le indicazioni precedenti, introduciamo sul piano le coordinate cartesiane (x, z) e consideriamo la trasformazione lineare

definita dagli allungamenti λ1 e λ3 lungo i rispettivi assi x e z.
La posizione della stella A è specificata sulla circonferenza per mezzo del raggio-vettore a = (x, z), mentre la posizione della “stella spostata” è contrassegnata con la B dal raggio-vettore b = (λ1x, λ3z). Il nostro obiettivo è quello di calcolare l'angolo Δψ in funzione della latitudine iniziale ψ e dei coefficienti di allungamento (compressione) λ1 e λ3.
8.6. La possibile stima della distorsione e la stabilità della datazione risultante.
Secondo i teoremi elementari della geometria analitica, cos Δψ è uguale al prodotto scalare (a, b) dei vettori a e b diviso per la lunghezza del vettore b. Il raggio della circonferenza OM viene naturalmente presunto uguale a 1, che può sempre essere ottenuto tramite la scelta della scala. Per cui,

Ora cerchiamo di trovare le stime numeriche effettive di ε. Tenete presente che λ3 / λ1 = 1 + ε, il che vuol dire che il valore di ε rappresenta il tasso di distorsione del sistema delle coordinate. I valori che utilizziamo nelle nostre formule sono comodi da esprimere in radianti. Per cui: 1° = π / 180; 1' = 1° / 60 = 3,14 / (60 × 180) ≈ 4,35 × 10–4, ossia 1' ≈ 0.00044.
Pertanto, per i valori sensibili di ε, ossia gli errori dello strumento non visibili a occhio nudo, le latitudini delle stelle che sono vicini al polo o all'eclittica sono solo leggermente distorte. La questione è che in questi casi sin2ψ tende a essere pari a zero, il che dovrebbe dirci che gli errori ragionevolmente possibili dello strumento non possono influenzare significativamente il risultato della misurazione delle stelle che possiedono valori latitudinali sia piccoli che grandi, in altre parole le latitudini vicine a 0° e 90°. Possiamo aspettarci le massime aberrazioni latitudinali dalle stelle situate a grande distanza sia dal polo che dal polo dell'eclittica.
Forniamo le stime quantitative precise utilizzando il materiale di un vero catalogo stellare: l'Almagesto, per esempio. Come si vede dalla Figura 7.27, il grafico della massima discrepanza latitudinale del kernel informativo dell'Almagesto cresce piuttosto rapidamente sia a sinistra che a destra dell'intervallo tra il 600 d.C. e il 1300 d.C. Ci si potrebbe chiedere se tenendo conto degli errori dello strumento ci consentirebbe di annullare o minimizzare questa discrepanza latitudinale intorno all'inizio della nuova era, che è l'epoca in cui fu creato l'Almagesto secondo la versione di Scaligero della cronologia.
In altre parole, ci chiediamo se si potesse trovare qualsiasi prova dell'ipotesi scaligeriana secondo cui il catalogo stellare dell'Almagesto sarebbe stato creato in un certo periodo vicino all'inizio della nuova era. Tuttavia, si presume che l'osservatore abbia usato uno strumento un po' deformato che è risultato nell'introduzione di un certo errore nelle latitudini stellari. Se tenessimo conto di questo errore, ci consentirebbe di datare il catalogo a un'epoca più vicina all'inizio della nuova era?
Dimostreremo che ciò è impossibile. Ipotizziamo che i risultati della misurazione siano stati compromessi dagli strumenti astronomici deformati e teniamo conto di questi errori al fine di minimizzare la discrepanza latitudinale del kernel informativo dell'Almagesto, supponendo che le stelle siano state osservate intorno all'inizio della nuova era. Tuttavia, avevamo già calcolato questa discrepanza piuttosto sostanziale: il suo minimo è di 35' per lo 0 d.C. Può essere corretto dalla scelta di un valore idoneo di ε?
In precedenza è stato dimostrato che la minimizzazione della discrepanza latitudinale per le stelle con valori latitudinali piccoli e grandi non è affatto possibile; tuttavia, potremmo provare con le stelle le cui latitudini sono vicine a 30° - 40°. Il kernel informativo del catalogo dell'Almagesto contiene Arturo; la sua latitudine corrisponde a 31 gradi. Inoltre, dal momento che Arturo possiede un'alta velocità di moto proprio, è il fattore principale per produrre la massima discrepanza latitudinale del kernel informativo all'inizio della nuova era. La Figura 7.31 dimostra che il grafico della discrepanza latitudinale di Arturo fa in modo che questa discrepanza raggiunga i 35' attorno all'inizio del periodo dopo Cristo. Quindi cerchiamo di indagare se sia possibile una sostanziale riduzione della discrepanza in prossimità della datazione di Scaligero del catalogo dell'Almagesto, supponendo che lo strumento dell'osservatore fosse deformato.
Calcoliamo il valore di ε. Come è stato detto in precedenza, il tasso di precisione Δ del catalogo dell'Almagesto equivale a 10' come dichiarato dal compilatore. Perciò, al fine di annullare la discrepanza latitudinale di Arturo, questa deve essere ridotta da 35' a 10', rendendola più piccola di un fattore di 25'. Quindi dobbiamo trovare quel valore di ε che renderà Δψ uguale a 25'. In radianti Δψ = 0,01. La formula di ε ci dice immediatamente questo

Pertanto, ε dovrebbe essere più o meno uguale a 0,023. Solo le distorsioni dello strumento potrebbero spiegare la discrepanza latitudinale di Arturo osservata nell'inizio dell'epoca dopo Cristo. Tuttavia, questo valore di ε è eccessivo; per esempio, se il raggio dell'astrolabio fosse uguale a 50 centimetri, lo strumento dovrebbe essere deformato in misura tale che uno dei semi-assi sarebbe uguale a 51 cm; vale a dire che l'errore deve manifestarsi come una deformazione di 1 cm! Difficilmente si può tollerare una precisione così bassa da uno strumento astronomico, altrimenti dovremmo supporre che all'epoca di Tolomeo anche le capriole erano più precise degli astrolabi.
8.7. La tabella dei valori numerici per le “distorsioni ellissoidali” possibili.
Prima abbiamo riportato la tabella dei valori esatti di distorsione derivanti dalle misurazioni della latitudine stellare realizzate con un certo strumento, ad esempio un astrolabio che aveva un anello latitudinale deformato. Facciamo notare che il tasso dell'errore latitudinale della stella A dipende anche dal valore della latitudine effettiva di A, come anche il valore di λ = R3 / R1. Qui R1 e R3 sono i semiassi latitudinali dell'anello ellissoidale dello strumento. Come sopra, supponiamo che λ = 1 + ε. Quindi, il valore di ε = 0 dovrà corrispondere all'anello ideale, quando l'ellisse diventerà una circonferenza. In questo caso le discrepanze devono essere uguali a zero per tutte le latitudini. Come si può vedere dalla Tabella 7.4, i valori massimi assoluti degli errori compaiono alla latitudine di 45 gradi, che è anche facile da dimostrare teoricamente. La Tabella 7.4 contiene i valori della differenza b' - b, dove b è il valore preciso della latitudine di una stella e b' il valore della latitudine misurata dai segni sugli anelli ellissoidali con il parametro λ = 1 + ε. I valori di b e ε sono le voci della tabella; i valori delle distorsioni b' - b sono stati calcolati quantitativamente con l'uso del computer.
La Tabella 7.4 mostra solo quale tasso di errore abbiamo considerato accettabile, sostituendo la trasformazione della griglia delle coordinate non lineari considerate sopra, per mezzo della sua parte lineare principale. Prendendo in considerazione questo errore non si influenzano le nostre conclusioni sull'impossibilità di concepire che lo strumento di Tolomeo sia stato deformato a tal punto da consentire un intervallo di datazione che copra l'epoca scaligeriana dell'Almagesto, ovvero il I-II secolo d.C.
8.8. Conclusioni.
- È teoricamente possibile che uno strumento astronomico deformato produca un sistema di coordinate spaziali soggetto a una certa trasformazione lineare.
- Si può teoricamente calcolare la dipendenza tra il coefficiente di distorsione dello strumento ε e l'errore risultante nella stima della latitudine stellare.
- I dati contenuti nei cataloghi veri (come ad esempio l'Almagesto) consentono la stima dei valori numerici di ε e Δψ.
- Nessuna deformazione sensibile dello strumento astronomico può spiegare il gigantesco errore latitudinale scoperto nel catalogo dell'Almagesto, supponendo che le osservazioni sono state condotte all'inizio della nuova era.
9. Il comportamento longitudinale delle stelle con nome dell’Almagesto.
Durante i nostri sforzi volti alla datazione, abbiamo considerato separatamente le latitudini e le longitudini del catalogo. Abbiamo scoperto che la precisione latitudinale dell'Almagesto è molto più alta di quella longitudinale. E' stata l'analisi delle latitudini che ci ha permesso di costruire un possibile intervallo informativo di datazione per il catalogo dell'Almagesto.
Ovviamente, abbiamo condotto tutti i calcoli necessari per verificare la datazione che finisce per usare le longitudini anziché le latitudini. Come ci si potrebbe aspettare se si fossero presi in considerazione i risultati della nostra analisi preliminare, è venuto fuori che non si può datare il catalogo dell'Almagesto in qualsiasi punto dell'intervallo tra 1000 d.C. e il 1900 d.C. tramite le longitudini stellari, poiché la loro precisione è troppo bassa.
Più avanti studieremo la possibilità di utilizzare sia le latitudini che le longitudini per datare il catalogo dell'Almagesto.
Ora consideriamo la datazione dell'Almagesto che finisce per usare come base le longitudini e non le latitudini.
Useremo Li (t, γ, φ) per riferirci alla latitudine della stella i tenendo conto degli angoli di rotazione della sfera celeste γ e φ. Tenete presente che queste indicazioni rappresentano la compensazione del possibile errore nella posizione dell'eclittica. L'errore è definito dai parametri γ e φ. Al fine di rendere più precise le nostre conclusioni, considereremo solo le 6 stelle con nome del catalogo dell'Almagesto provenienti dall'area celeste Zod A e dalle sue immediate vicinanze, ovvero Arturo, Regolo, Antares, Spiga, Aselli e Procione. Nel Capitolo 6 siamo riusciti a capire che per queste sei stelle l'errore di gruppo γ coincide con il valore di γstatZod A.
Calcoliamo i valori di Li (t, γstatZod A (t), φstatZod A (t)) per queste stelle, ossia le loro latitudini dopo la compensazione del rispettivo errore di gruppo per l'epoca t. Ovviamente, qui si può fare un errore significativo per almeno due motivi. Il primo è che il parametro φ influenza notevolmente i valori delle longitudini. Allo stesso tempo, abbiamo osservato che non c'è stabilità nella stima di questo parametro; pertanto, non si può assolutamente garantire che sia lo stesso per tutte e sei le stelle e che sia uguale a φstatZod A. La seconda ragione è la seguente: prima non abbiamo considerato gli errori di gruppo nelle longitudini, che potrebbero benissimo esserci, vedere [1339]. La loro analisi porta alla necessità di introdurre un altro valore che renderebbe parametrizzabile l'errore di gruppo. Il parametro τ può servire a tale scopo, vedere il Capitolo 3. Rappresenta l'angolo di rotazione della sfera celeste attorno ai due nuovi poli dell'eclittica definiti dai parametri γ e φ.
Definiamo ΔLi (t, γstatZod A (t), φstatZod A (t)) - li. Se tracciassimo il grafico di funzione per ΔLi(t), potremmo rappresentarlo con la somma di una funzione quasi lineare (la variazione longitudinale uniforme derivante dalla precessione) e la “aggiunta” irregolare corrispondente a tutti i tipi di errori.
Pertanto, al fine di escludere dalla considerazione gli effetti della precessione, così come il possibile errore sistematico τ, introduciamo il valore
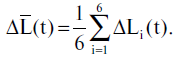
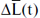 è un valore piuttosto preciso che misura gli spostamenti longitudinali delle 6 stelle in esame risultanti dalla precessione. Supponiamo che
è un valore piuttosto preciso che misura gli spostamenti longitudinali delle 6 stelle in esame risultanti dalla precessione. Supponiamo che
ΔLi0 (t) = ΔLi (t) - 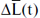
La precessione non ha praticamente nessun effetto sul valore
Nella Figura 7.38 si possono vedere i cambiamenti di ΔLi0 (t) come funzioni della presunta datazione per le sei stelle dell'Almagesto prese in considerazione. La prima implicazione dell'immagine è la bassa velocità di variazione dei valori di ΔLi0 (t) nel corso del tempo. Dopo la compensazione della precessione, le stelle “veloci” dell'Almagesto risultano essere molto “lente” per quanto riguarda le longitudini. Per esempio, le velocità di variazione della longitudine di Arturo e Regolo sono quasi uguali tra loro. Procione diventa la stella più veloce delle sei; tuttavia, la sua longitudine oltre i 3000 anni (tra il 1100 a.C. e il 1900 d.C.) è modificata solo di 17', che è leggermente superiore a 5' per millennio. Questi lenti cambiamenti longitudinali sono ovviamente insufficienti per una datazione informativa.
Nella Figura 7.39 possiamo vedere due grafici che potrebbero teoricamente servire ai fini della nostra datazione. Tuttavia, il comportamento di questi grafici testimonia la loro totale inutilità in questa veste. Consideriamo in particolare le due seguenti funzioni:
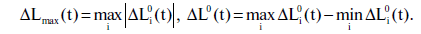
La prima corrisponde alla massima discrepanza longitudinale tra le stelle effettive in fase di studio e quelle trovate nell'Almagesto. Il valore assoluto dell'aberrazione si considera che tenga conto della precessione. La seconda funzione non dipende dalla precessione, in quanto è la differenza tra l'aberrazione minima e quella massima. La funzione di ΔLmax(t) raggiunge il suo minimo a t = 15, ossia nel 400 d.C., mentre la funzione ΔL0(t) lo raggiunge a t = 32.5, che corrisponde approssimativamente al 2350 a.C. Entrambe le funzioni assumono dei valori considerevolmente grandi (ΔL0(t) ≥ 25' e ΔL0(t) ≥ 30' a partire dall'epoca scaligeriana di Ipparco). Infine, ΔLmax(t) ≥ 17'. Tutto ciò dimostra che la precisione latitudinale è troppo bassa rispetto alle velocità di moto proprio. Non ci offre alcuna dea di quale potrebbe essere stata la vera data di osservazione.

Figura 7.38.
Le longitudini delle sei stelle con nome
(Arturo = 110 nella numerazione di Bailey, Regolo = 469, Procione = 848,
Antares = 553, Spiga = 510, Aselli = 452) e il loro comportamento.
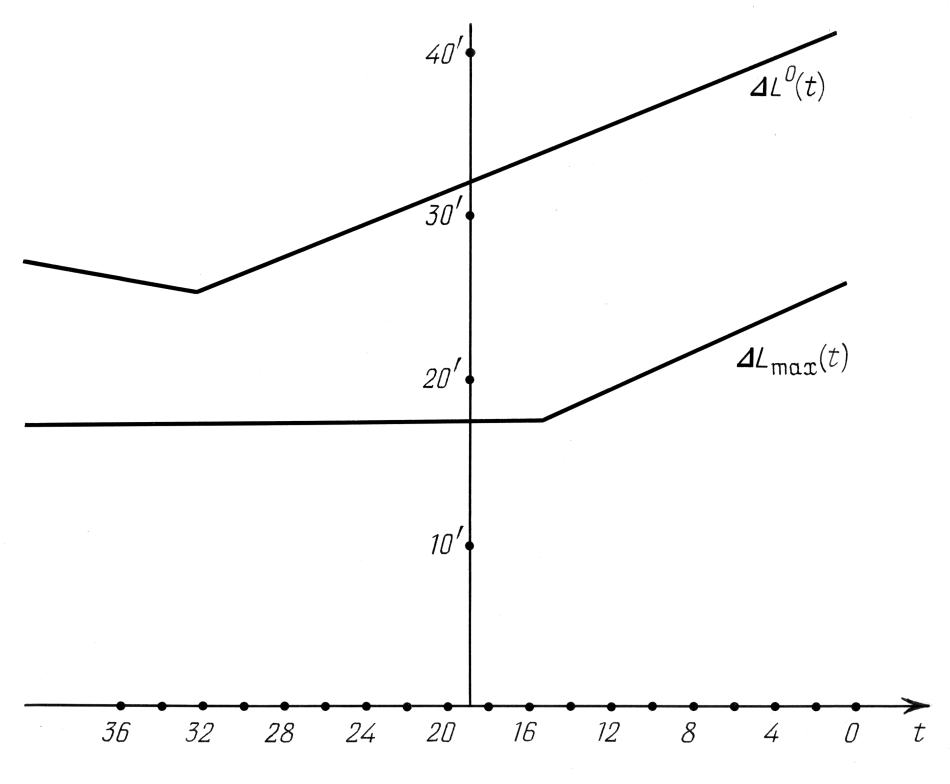
Figura 7.39.
Il comportamento delle funzioni ΔLmax (t) e ΔL0(t).
I nostri calcoli hanno quindi confermato che le longitudini del catalogo dell'Almagesto non sono particolarmente informative a causa del loro basso tasso di precisione. A quanto pare, la vera ragione è stata scoperta da R. Newton ([614]). Afferma che le longitudini dell'Almagesto sono state contraffatte da qualcuno (vedi anche il Capitolo 2). Non abbiamo condotto alcuna ricerca approfondita in questa direzione: è anche possibile che l'analisi statistica delle longitudini rilevi dei modelli consecutivi nel loro comportamento. Ciò potrebbe dimostrare l'esistenza di errori di gruppo in alcune parti del catalogo dell'Almagesto, per esempio. Tuttavia, a prescindere dal fatto che ciò si riveli essere vero o no, la nostra ricerca dimostra che non ha senso usare le longitudini per ottenere una datazione più precisa del catalogo dell'Almagesto.
10. Il comportamento delle discrepanze d’arco nella configurazione che comprende il kernel informativo dell’Almagesto.
Nel Capitolo 3 abbiamo già menzionato la possibilità di datare il catalogo tramite un'analisi comparativa di due configurazioni, una delle quali è immobile e composta dalle stelle dell'Almagesto, mentre l'altra è mobile e composta da stelle moderne. Abbiamo fatto notare che questo confronto non richiede alcun riferimento alla teoria di Newcomb; per esempio, se dobbiamo considerare solo le differenze della distanza dell'arco. L'uso di questo metodo ci consente di affrontare i seguenti ostacoli: i possibili errori nell'identificazione della stella e la bassa precisione nella misurazione delle coordinate che porta a intervalli di datazione eccessivamente grandi, come pure l'impossibilità di distinguere con questo approccio le coordinate misurate in modo preciso da quelle imprecise: le latitudini e le longitudini, per esempio.
Se dovessimo scegliere il kernel informativo del catalogo dell'Almagesto come configurazione da studiare, i primi due ostacoli diventerebbero irrilevanti. Infatti, l'identità delle stelle in questione è certa e la nostra ipotesi primaria implica che la loro precisione sia abbastanza alto, almeno per quanto riguarda la latitudine. A parte questo, il kernel informativo contiene due stelle che si muovono a velocità sufficientemente elevate: Arturo e Procione. È ovvio che l'errore sconosciuto nelle misurazioni della longitudine possa portare ad errori di datazione inestimabili. Tuttavia, il fatto che con questo approccio non abbiamo bisogno di considerare gli errori di gruppo, rende più considerevoli i corrispondenti calcoli. Tuttavia, purtroppo è impossibile stimare gli errori di questi calcoli (almeno, basando tali stime sulla nostra ricerca).
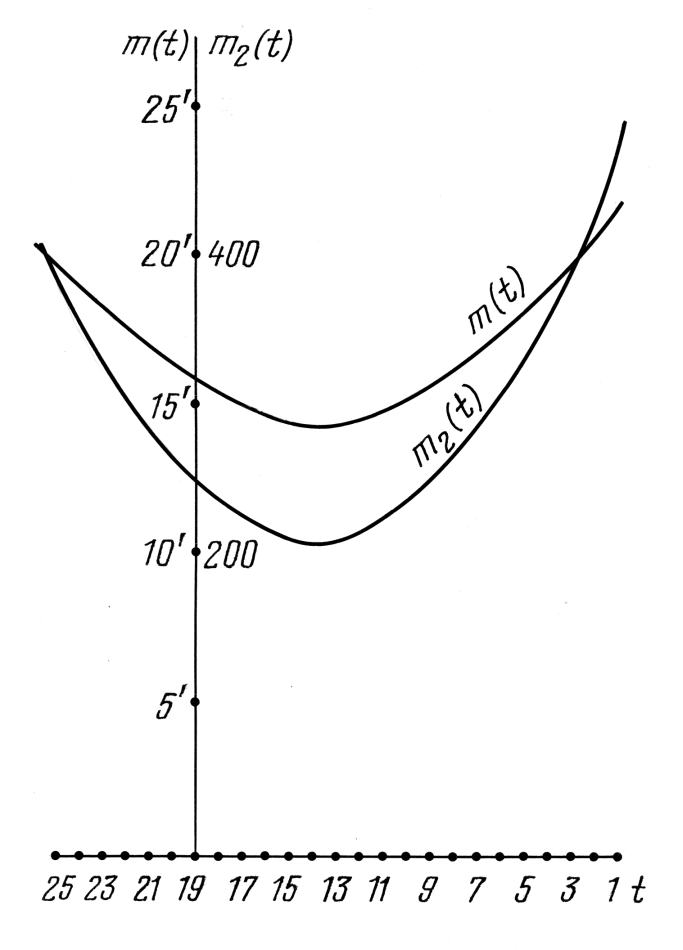
Figura 7.40.
I grafici m2(t) e m(t) che caratterizzano la variazione
nella configurazione delle 8 stelle con nome dell'Almagesto.
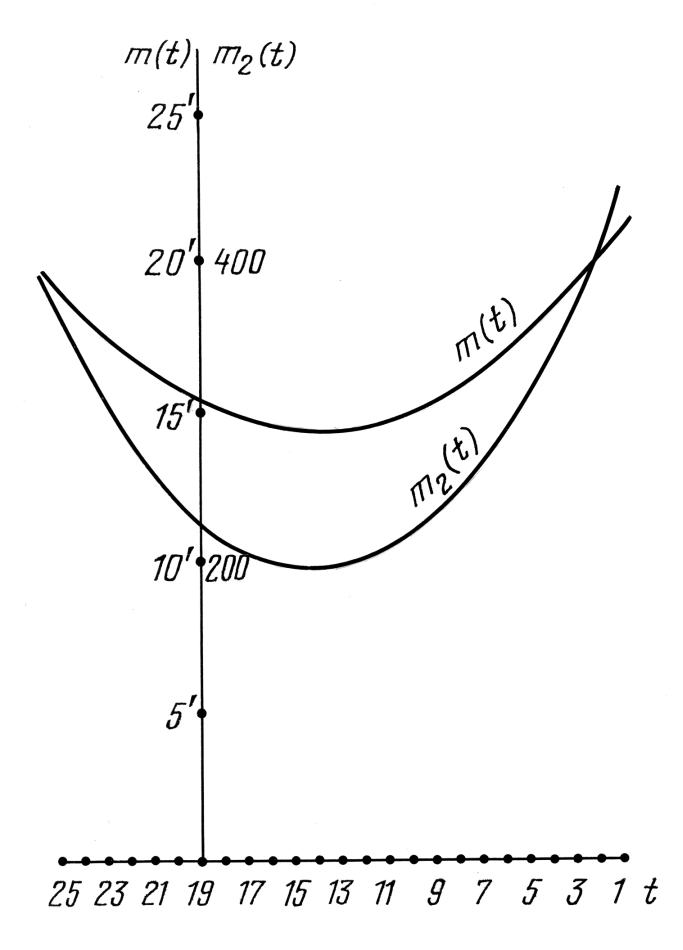
Figura 7.41.
. I grafici m2(t) e m(t) che caratterizzano l’alterazione
nella configurazione delle 6 stelle con nome dell'Almagesto.
Riportiamo i risultati dei calcoli che abbiamo condotto in questa direzione per 8 e 6 stelle con nome dell'Almagesto.
Mettiamo che lijA rappresenti la distanza d'arco tra le stelle dell'Almagesto i e j. Presumeremo che lijt rappresenti la distanza simile tra le stelle moderne, calcolata per il momento di osservazione t = 1,…, 25. Il numero di stelle nella configurazione in studio sarà rappresentato da n. Segniamo
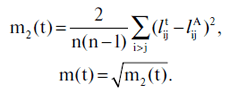
Il valore di m(t) può essere considerato come la distanza generalizzata tra la configurazione calcolata per l'epoca t e la rispettiva configurazione delle stelle dell'Almagesto. I punti minimi delle funzioni m2(t) e m(t) devono essere vicini alla data di compilazione del catalogo. Nella Figura 7.40 si possono vedere i grafici delle funzioni m2(t) e m(t) per la configurazione di 8 stelle con nome dell'Almagesto, mentre nella Figura 7.41 gli stessi grafici per la configurazione di 6 stelle con nome.
È ovvio che in entrambi i casi possiamo vedere un punto minimo ben distinto che cade su t = 14 (il 500 d.C.). In entrambi i casi, il valore minimo di m(t) è pari più o meno a 14', che corrisponde al tasso medio di precisione di 10' per ogni coordinata. La datazione del 500 d.C. si trova molto chiaramente a una distanza considerevole dalla data di Scaligero della compilazione dell'Almagesto.
Il fatto che la datazione a cui siamo giunti, il 500 d.C., sia più antica rispetto all'intervallo di datazione calcolato sopra con l'aiuto dell'analisi latitudinale, è spiegato dal fatto che l'errore longitudinale preso indipendentemente dalle latitudini assume il valore minimo in t ≈ 31, ossia il 1200 a.C., vedere il paragrafo 9. La datazione dell'Almagesto al 1200 a.C. ovviamente non ha alcun senso, tuttavia bisogna tener presente che il minimo della discrepanza longitudinale media si manifesta molto male, per cui il tasso di precisione di questa datazione potrebbe essere pari a diversi millenni. In altre parole non contraddice nulla, vedere le Figure. 7.38 e 7.39. D'altra parte, il minimo della discrepanza latitudinale avviene in t = 10, ossia il 900 d.C. ed è molto più ovvio. Tutto ciò risulta nel minimo delle aberrazioni dell'arco medio quadratico che cade nel punto intermedio t = 14, ovvero il 500 d.C. Questa datazione è molto più vicina al punto minimo latitudinale rispetto che a quello longitudinale.
11. Conclusioni.
- La stima della datazione del catalogo dell'Almagesto con le procedure statistiche e geometriche che abbiamo suggerito si trova nell'intervallo tra il 600 d.C. e il 1300 d.C.
- Le datazioni precedenti il 600 d.C. non ci offrono alcuna opportunità di far coincidere la sfera celeste effettiva e l'atlante stellare dell'Almagesto, con le discrepanze latitudinali di tutte le stelle che formano il kernel informativo dell'Almagesto che rimangono sotto la soglia dei 10".
- Persino se dovessimo presumere che la precisione del catalogo dell'Almagesto sia pari a 15'e non a 10', l'epoca scaligeriana di Tolomeo (I-II secolo d.C.) rimarrebbe al di fuori del possibile intervallo di datazione.
- Anche cambiando il contingente del kernel informativo dell'Almagesto non porterebbe all'inclusione del periodo di vita di Tolomeo (secondo Scaligero) nel possibile intervallo di datazione.
- Nemmeno gli errori effettivi nella fabbricazione di strumenti astronomici che portano a distorsioni non lineari della sfera celeste nel catalogo, sono in grado i spostare o ampliare abbastanza l'intervallo di datazione, tanto da includere l'epoca scaligeriana di Tolomeo.