В.В.Калашников, Г.В.Носовский, А.Т.Фоменко
ЗВЕЗДЫ СВИДЕТЕЛЬСТВУЮТ.
Астрономический анализ хронологии.
Датировка Альмагеста Птолемея. Коперник, Тихо Браге и "античный" Гиппарх.

Том 3 , книга 1

Глава 6.
СТАТИСТИЧЕСКИЕ И ТОЧНОСТНЫЕ СВОЙСТВА КАТАЛОГА АЛЬМАГЕСТА.

1. ВВОДНЫЕ ЗАМЕЧАНИЯ.

В предыдущих главах мы выяснили, что одной из узловых трудностей при датировании Альмагеста по собственным движениям звезд является проблема реальной точности звездных широт каталога Альмагеста в различных областях неба. Таким образом, необходим тщательный анализ ошибок звездных координат как каталога в целом, так и его частей по отдельности. Предварительный, довольно грубый анализ уже проведен выше, в главах 2 и 4.

Основным инструментом этой главы будут методы определения систематических ошибок звездных координат, описанные в главе 5. Прежде всего, мы покажем, что выделенные нами выше семь областей звездного атласа Альмагеста действительно отличаются друг от друга как величиной систематической ошибки, так и случайными погрешностями измерений. Мы найдем для этих областей ошибки в положении полюса эклиптики и величины остаточных среднеквадратичных ошибок звездных координат. Кроме того, в каждой области будут построены доверительные интервалы для параметров систематической ошибки γ_stat и φ_stat.

Далее, мы проанализируем сравнительно малые участки звездного неба -- созвездия и окружения отдельных звезд. Цель этого анализа -- убедиться, что найденные значения γ_stat и φ_stat действительно имеют природу систематических ошибок в достаточно больших частях каталога Альмагеста, а не являются результатом наложения множества групповых ошибок, различных для разных небольших групп звезд.

В результате, мы выделим хорошо измеренную Птолемеем область звездного неба. Забегая вперед, отметим, что она оказалась довольно значительной. Наша датировка каталога Альмагеста будет основываться на координатах звезд именно в этой, хорошо измеренной им области.

 

2. СЕМЬ ОБЛАСТЕЙ ЗВЕЗДНОГО НЕБА.

2.1. ХАРАКТЕРИСТИКА ОБНАРУЖЕННЫХ СЕМИ ОБЛАСТЕЙ В АТЛАСЕ АЛЬМАГЕСТА.

В главе 2 были описаны семь областей звездного неба, естественным образом выделяющиеся на небе, а также отчетливо "проявляющие себя" в каталоге Альмагеста, рис.6.1.

В этой главе мы проанализируем птолемеевские координаты в общей сложности 864 звезд из этих областей. Эти 864 звезды оставлены нами из примерно 1000 звезд каталога Альмагеста после следующего отбора. Во-первых, по причинам, разъясненным в главе 2, исключены из рассмотрения так называемые звезды-информаты, то есть звезды, не входящие в канонические созвездия. Во-вторых, мы исключили также звезды-"выбросы", и неоднозначно отождествляемые звезды. Табл.6.1 содержит точные указания -- какие именно звезды Альмагеста входят в ту или иную область и какое количество звезд осталось в каждой области после указанной "чистки". В этой таблице для звезд использованы номера Байли, то есть сквозные номера в каталоге Альмагеста.

Таблица 6.1.

Обратимся к рис.6.1, схематично изображающему разбиение неба на указанные области. На нем черными точками отмечены все 12 именных звезд Альмагеста. Легко видеть, что контур области A совершенно явно очерчен именными звездами. Возникает впечатление, что Птолемей придавал области неба A какое-то особое значение. Это подтверждается и нашим предварительным анализом в главе 2. Как мы увидим в дальнейшем, часть A оказывается самой важной для датировки. Отметим, между прочим, что именно она содержит полюс мира N и полюс эклиптики P.

Именные звезды, окаймляющие область A, возможно, служили опорными для наблюдений Птолемея. Отправляясь от них, он двигался внутрь части неба A, измеряя координаты остальных звезд. При движении от звезды к звезде неизбежно накапливались ошибки измерений. Поэтому можно ожидать, что звезды области неба A, лежащие вне Зодиака, будут в среднем измерены чуть хуже, чем зодиакальные звезды. Дело в том, что половина именных звезд Альмагеста, -- 6 из 12-ти -- либо лежат на Зодиаке, либо находятся в непосредственной близости от него. На Зодиаке расположены Регул, Спика, Антарес, Превиндемиатрикс, Аселли. Непосредственно примыкает к Зодиаку Процион.

 

2.2. РАСПОЛОЖЕНИЕ ПОЛЮСОВ ЭКЛИПТИКИ ДЛЯ КАЖДОЙ ИЗ СЕМИ ОБЛАСТЕЙ ЗВЕЗДНОГО АТЛАСА АЛЬМАГЕСТА.

Найдем сначала расположение полюсов эклиптики для каждой из семи выделенных нами областей неба в Альмагесте. В главе 5 показано, что положение полюса эклиптики относительно звезд каталога задается параметрами γ_stat и φ_stat. Эти параметры определяются по каталогу методом наименьших квадратов по формулам (5.3.6) и (5.3.7).

Рассчитаем по формулам (5.3.6) и (5.3.7) значения параметров γ_stat и φ_stat для каждой из семи областей неба по отдельности. После этого изобразим соответствующее каждой области положение полюса эклиптики на рис.6.2. Кроме того, на этом же рисунке изобразим движение реального полюса эклиптики P(t) при изменении предполагаемой датировки.

На рис.6.2 показан в качестве примера отрезок, соединяющий полюс эклиптики для части неба B с реальным полюсом эклиптики в эпоху t=10, который обозначен P(10). Длина этого отрезка равна величине γ_stat^B(10). Угол между этим отрезком и прямой, изображающей дугу D(10)D'(10), определение которой было дано в связи с рис.5.4.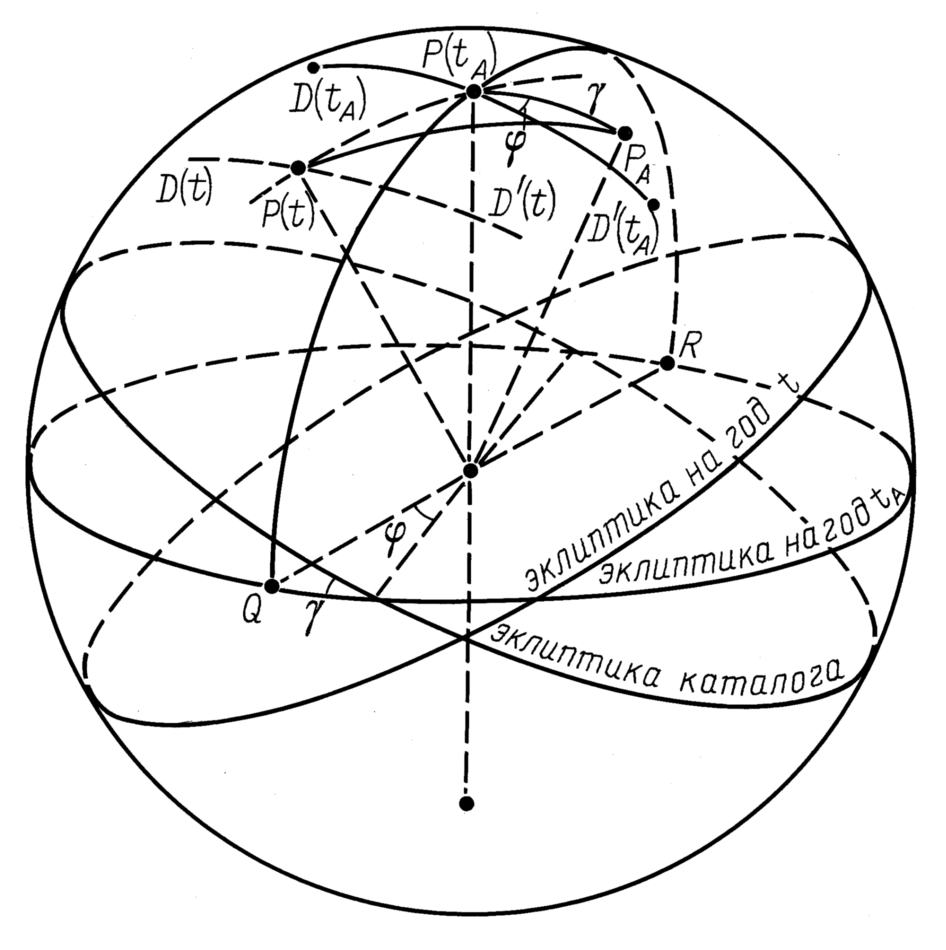 и рис.5.5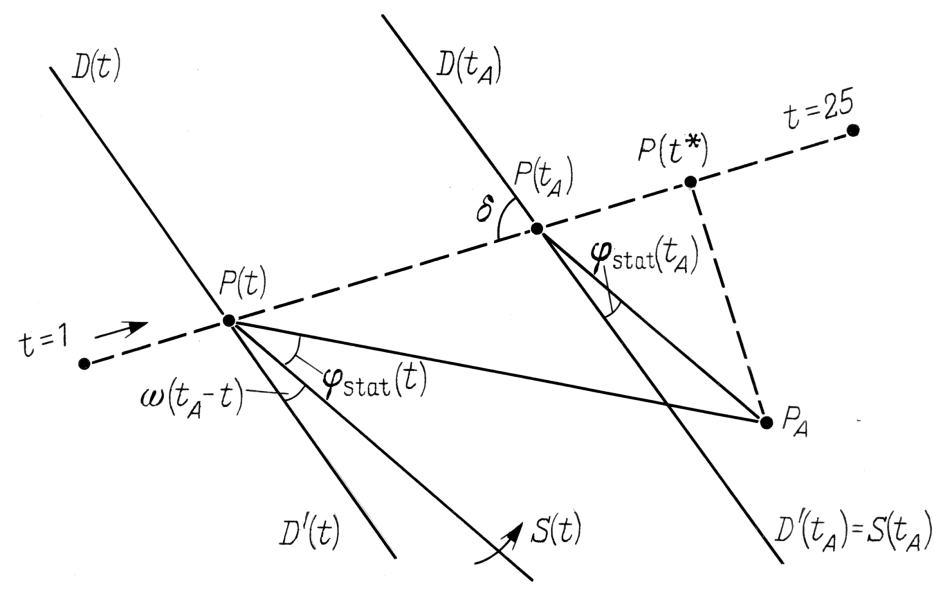, равен φ_stat^B(10). Естественно, в качестве t можно взять любую другую эпоху, а вместо области B любую другую область -- и "считать" с рис.6.2 соответствующие значения γ_stat и φ_stat.

В табл.6.2 приведены рассчитанные нами значения γ_stat(18) и φ_stat(18) для всех семи областей неба. Эти значения однозначно задают положение полюса "эклиптики наблюдателя" для каждой области по отдельности. Впрочем, мы могли бы с тем же успехом взять любую пару значений γ_stat(t), φ_stat(t) для произвольного t. См. раздел 5.4. Кроме того, в табл.6.2 приведены исходная σ_init(18) и остаточная σ_min среднеквадратичные широтные невязки, получившиеся после компенсации систематической ошибки. См. формулы (5.3.2), (5.3.3). В разделе 5.4 мы показали, что σ_min не зависит от рассматриваемого момента времени t, если пренебречь слабым влиянием собственного движения звезд. Таким образом, σ_min задается лишь положением полюса эклиптики, статистически определяемого по данной группе звезд Альмагеста.

Таблица 6.2.

По поводу собственного движения звезд отметим, что оно практически не влияет ни на оценку систематической ошибки γ_stat(t),φ_stat(t), ни на остаточную среднеквадратичную погрешность звездных координат в каталоге Альмагеста. Поэтому о влиянии собственных движений мы здесь пока можем не говорить. Хотя, конечно, в наших расчетах оно всегда учитывалось.

Значение t=18 выбрано в табл.6.2 лишь по причине соответствия этого момента времени скалигеровской датировке Альмагеста.

Далее, в табл.6.2 приведены следующие статистические характеристики точности звездных координат Альмагеста. Величина p_init(18) -- это доля звезд, получивших при датировке каталога 100-м годом н.э. (t=18) широтную невязку не более 10'. Напомним, 10' -- это цена деления шкалы каталога Альмагеста. Величина p_min -- это доля звезд, получивших широтную невязку не более 10' после компенсации систематической ошибки. Для рассматриваемых здесь больших совокупностей звезд эта величина от датировки наблюдений практически не зависит.

Показанное на рис.6.2 расположение статистически определяемых полюсов Альмагеста по отношению к траектории движения истинного полюса говорит о том, что систематическая ошибка каталога Альмагеста во всех областях неба, кроме области C, "удревняет" каталог даже по сравнению со временем Гиппарха. Напротив, минимум систематической ошибки в области неба C приходится на t ≈ 10, то есть на ≈ 900 год н.э. Однако, как указывалось ранее, расположение полюса "эклиптики Птолемея" не имеет никакого отношения к дате составления каталога. Это расположение указывает лишь на характер и величину систематической ошибки, совершенной Птолемеем при измерении координат звезд в той или иной части неба.

Из рис.6.2 следует также, что статистически определяемые положения полюса для областей A, Zod A, Zod B расположены достаточно близко друг к другу, то есть, в этих частях неба Птолемеем сделана, по-видимому, одна и та же систематическая ошибка. Мы вернемся к этому ниже при анализе отдельных созвездий Альмагеста. Далее, полюс эклиптики, определяемый по области В каталога Альмагеста, как видно из рис.6.2, тоже расположен рядом с полюсом для групп A, Zod A, Zod B. Несколько дальше отстоит положение полюса для области M и еще дальше -- для D. По-видимому, в областях M и D систематическая ошибка Альмагеста другая, отличная, от ошибки в области Zod A. Явным "выбросом" на рис.6.2 выглядит область C.

 

2.3. ВЫЧИСЛЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ.

В предыдущем разделе, для неизвестных нам параметров систематической ошибки каталога Альмагеста γ и φ вычислены точечные статистические оценки γ_stat и φ_stat. Найдем теперь соответствующие доверительные интервалы для γ и φ. Определение доверительных интервалов мы уже напоминали в разделе 5.5.

Представим результат в наглядной форме. Сначала для каждой из рассматриваемых областей неба построим графики зависимости от t оценок γ_stat(t) и φ_stat(t), 1 ≤ t ≤ 25. Затем изобразим на получившихся графиках по'лосы, вертикальными сечениями которых являются доверительные интервалы I_γ(ε), I_φ(ε) с уровнем доверия ε=0,1. Доверительные интервалы мы рассчитаем по формулам (5.5.10) и (5.5.11).

Результат расчетов показан на рис.6.3, рис.6.4, рис.6.5, рис.6.6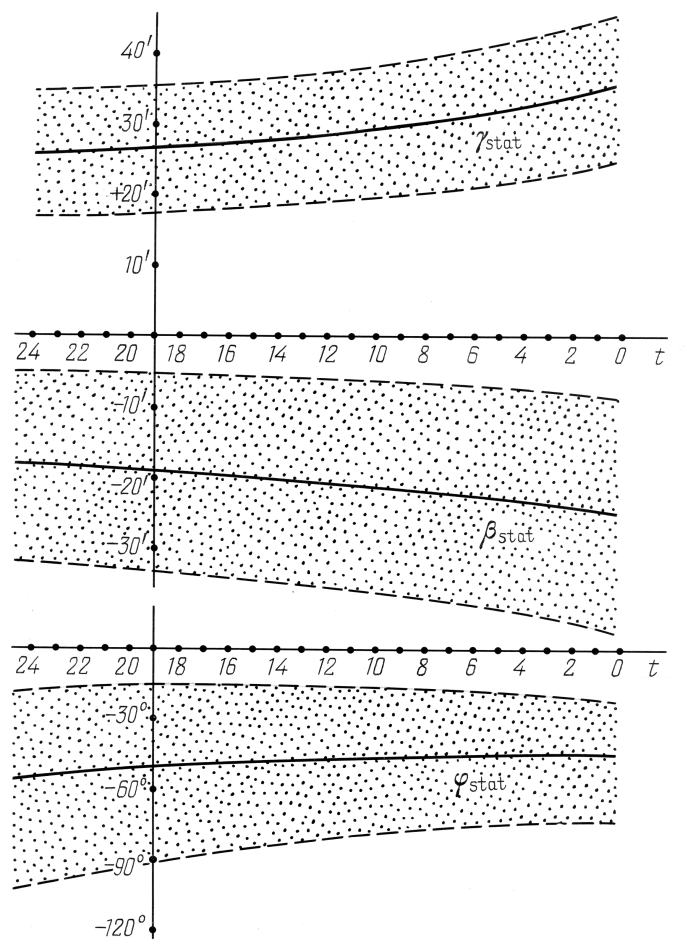, рис.6.7, рис.6.8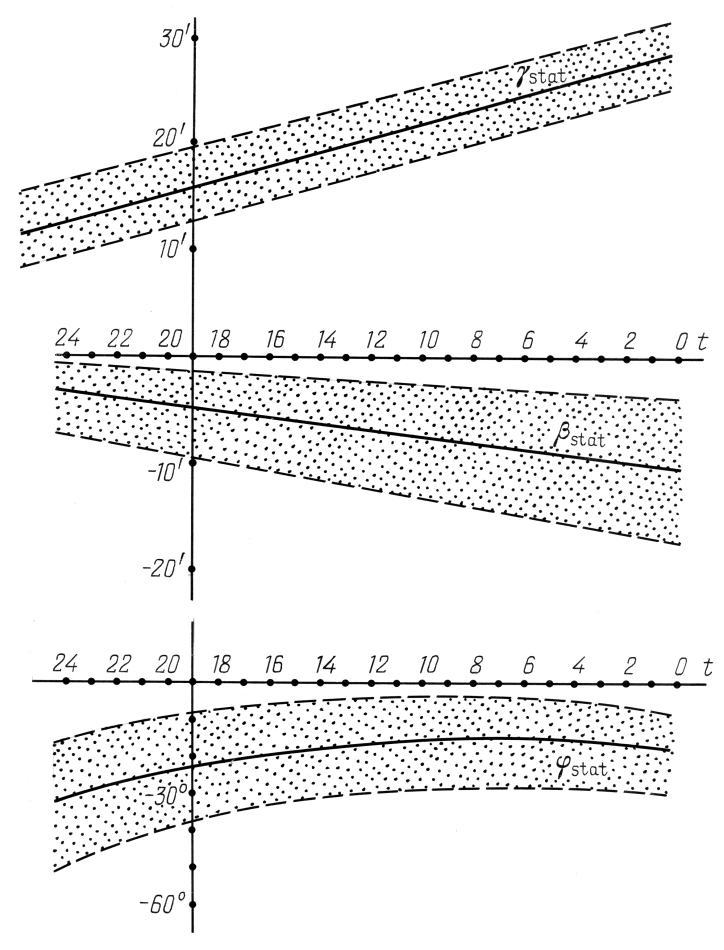, рис.6.9. Более полная информация о границах доверительных интервалов для различных уровней доверия ε и двух значений предполагаемой датировки каталога Альмагеста, -- для t=7(1200 г.н.э.) и t=18(100 г.н.э.) -- содержится в табл.6.3. В ней приведены значения полуширины доверительных интервалов I_γ(ε). Напомним, что центром доверительного интервала для γ при каждом фиксированном t является несмещенная оценка γ_stat(t). См. раздел 5.5. Доверительный интервал I_φ(ε) для φ располагается, вообще говоря, асимметрично относительно φ_stat(t), поскольку эта оценка может быть смещена. Однако указанная асимметрия достаточно мала и приближенно можно считать φ_stat(t) серединой доверительного интервала. Через x_ε^γ в таблице обозначена полуширина интервала I_γ(ε), а через x_ε^φ -- полуширина интервала I_φ(ε).

Таблица 6.3.

 

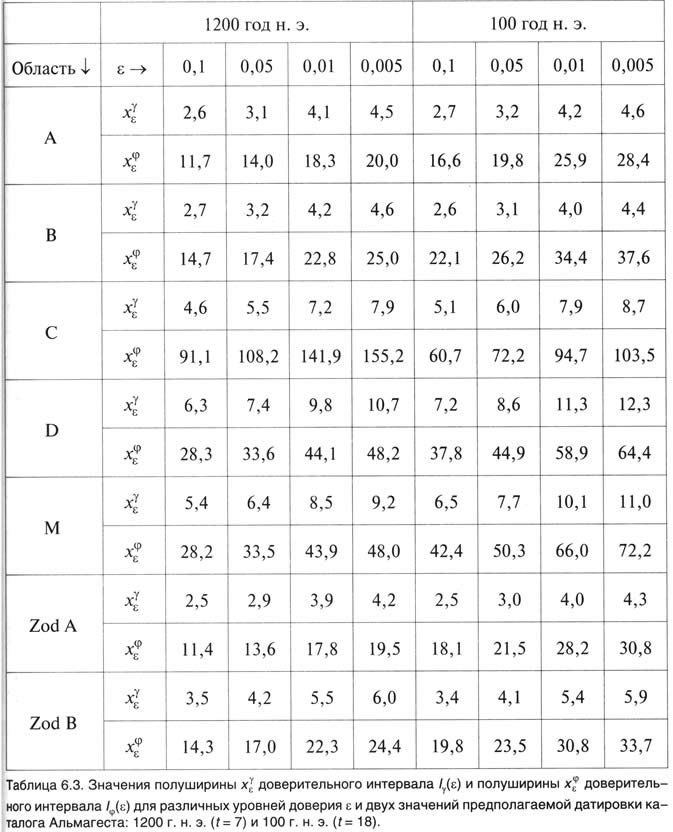
Цифры, приведенные в табл.6.2 и табл.6.3, позволяют сделать следующие выводы. Наиболее точно измерены в Альмагесте звезды из области неба Zod A. Это видно из того, что компенсация обнаруженной систематической ошибки для этой группы звезд позволила снизить среднеквадратичную ошибку до 12,8'. При этом оказалось, что около 64% звезд получили после компенсации широтную невязку менее 10'.

Следующей по точности группой звезд в Альмагесте является область A. Там среднеквадратичная широтная невязка снизилась после устранения систематической ошибки до 16,5'. При этом число звезд, имеющих широтную невязку меньше 10', возросло в этой области более чем до 50%.

Доверительные интервалы I_φ(ε) и I_γ(ε) для областей неба Zod A и A оказались близки по размерам. См. табл.6.3. Хотя точность измерений в области неба Zod A выше, чем в области A. Это объясняется разным числом звезд в этих областях. Размер доверительного интервала тем больше, чем меньше звезд. И тем меньше, чем выше точность измерений.

Данные табл.6.2 подтверждают претензии Птолемея на точность в 10'. По крайней мере -- для широт звезд.

Следующими по точности измерений оказываются группы звезд Альмагеста в частях неба B и Zod B. Их точностные характеристики весьма близки. Остаточная среднеквадратичная ошибка равняется приблизительно 19'. Звезды с широтной невязкой меньше 10' составляют около 44% в этих группах. Положения полюса эклиптики, определяемые по этим частям неба в Альмагесте, хотя "на глаз" и близки к положениям полюса для A и Zod A, но попадают в соответствующие доверительные полосы лишь при достаточно малых значениях ε ≈ 0,01. Это означает, что систематические ошибки в областях неба B и Zod B могут отличаться от ошибок в областях неба A и Zod A. Кроме того, в частях неба A и Zod A звезды измерены существенно точнее, чем в областях неба B и Zod B. Ниже мы приведем дополнительные аргументы, подтверждающие это обстоятельство.

Звезды в областях неба C, D, М измерены в Альмагесте хуже, чем в частях неба A и B. Более того, в этих областях значения оценок γ_stat и φ_stat попадают в доверительные интервалы для γ_stat и φ_stat по областям неба A, Zod A, B и Zod B лишь при достаточно малых ε. Это означает, что мы обязаны допустить в C, D, М наличие таких систематических ошибок Альмагеста, которые отличаются от систематической ошибки в областях A, Zod A, B и Zod B.

При анализе табл.6.2 и табл.6.3 уже возникал вопрос о том, какое изменение среднеквадратичной ошибки следует считать большим, а какое - малым. Для ответа на вопрос воспользуемся анализом чувствительности, проведенным в главе 5. Схема решения иллюстрируется на рис.6.10.

На координатной плоскости (γ, φ) изобразим эллипсоидальные линии уровней функции σ²(γ,φ,t), см. формулу (5.3.9). На этой же плоскости изобразим прямоугольник R(ε), имеющий координатные проекции I_γ(ε) и I_φ(ε). На рис.6.10 это -- заштрихованный прямоугольник. Тогда вероятность того, что истинное значение систематической ошибки (γ, φ) лежит в этом прямоугольнике, не меньше, чем 1-2ε. Найдем σ²_max(ε)=max σ²(γ, φ,t), где максимум берется по всем парам (γ,φ)∈ R(ε). Найденная величина σ_max(ε) определяет допустимую, -- с уровнем доверия 1-2ε, -- среднеквадратичную широтную невязку, а разность σ_max(ε) - σ_min определяет допустимое увеличение среднеквадратичной невязки из-за неточности оценивания параметров γ и φ значениями γ_stat и φ_stat.

В табл.6.4 для областей неба A и Zod A приведены величины a₁₁, a₁₂, a₂₂ на момент t=18, определяющие линии уровня среднеквадратичных ошибок. Линии уровня определяются формулой (5.3.9), в которой γ надо измерять в дуговых минутах, а φ -- в градусах. В таблице приведены также величины Δσ=σ_max(ε)-σ_min, рассчитанные для "крайних" значений ε=0,1 и ε=0,005. Отметим, что полученные величины, оказывается, мало меняются со временем. Эти цифры показывают уверенное разделение по точности областей неба A и Zod A, с одной стороны, и областей неба B и Zod B -- с другой. В самом деле, даже при уровне доверия 1-2ε=0,99 среднеквадратичная ошибка в доверительной области, построенной для области Zod A, не достигает минимального значения ошибки, полученного для областей неба B и Zod B.

Таблица 6.4.

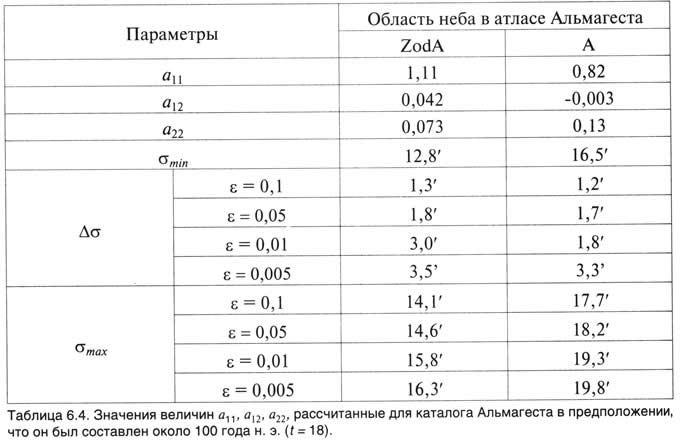
Аналогичное утверждение верно и для части неба A. Хотя σ_max^A для области неба A и больше σ_min^B, но это превышение происходит лишь при ε ≤ 0,01. При остальных значениях уровни ошибок в областях неба A и B следует считать существенно различными, то есть, разделяемыми статистическим критерием. Отметим здесь же, что точно так же звезды из группы Zod A, уверенно отличаются по точности от звезд из области неба A, так как при всех рассмотренных значениях ε величина σ_max, найденная для Zod A, является меньшей, чем σ_min, полученная для части неба A.

Далее, рис.6.3 показывает, что параметр φ_stat определяется недостаточно устойчиво, особенно для "плохих" в Альмагесте областей неба C, D, M. Об этом говорят размеры доверительных интервалов I_φ(ε). Так, для области C полная ширина этого интервала превышает 180 градусов!