Глава 7.
ДАТИРОВКА ЗВЕЗДНОГО КАТАЛОГА АЛЬМАГЕСТА.
СТАТИСТИЧЕСКИЙ И ГЕОМЕТРИЧЕСКИЙ МЕТОДЫ.
9. ПОВЕДЕНИЕ ДОЛГОТ ИМЕННЫХ ЗВЕЗД АЛЬМАГЕСТА.
При датировке каталога Альмагеста мы исследовали отдельно широты и долготы каталога. Выяснилось, что точность широт в Альмагесте существенно выше, чем точность долгот. Именно анализ широт позволил нам получить содержательный интервал возможных датировок каталога Альмагеста.
Естественно, мы провели все необходимые вычисления и проверили -- какая датировка получается, если вместо широт использовать долготы. Как и следовало ожидать по итогам нашего предварительного анализа, оказалось, что датировать каталог Альмагеста в пределах интервала времени от 1000 года до н.э. до 1900 года н.э., основываясь лишь на долготах звезд, не удается. Причина -- слишком низкая точность долгот звезд в Альмагесте.
Возможность датировки каталога Альмагеста на основе совместного учета широт и долгот мы рассмотрим в следующем разделе.
Итак, посмотрим, какая датировка Альмагеста получается, если за основу брать не широты, а долготы звезд.
Обозначим через Li(t, γ, φ) значение долготы i-й звезды с учетом поворота звездной сферы на углы γ и φ. Это означает, напомним, что мы компенсируем возможную ошибку в положении эклиптики. Ошибка задается параметрами γ и φ. Для того, чтобы по возможности повысить точность выводов, рассмотрим лишь 6 именных звезд каталога Альмагеста, лежащих в области Zod A и в ее непосредственной окрестности. Это -- Арктур, Регул, Антарес, Спика, Аселли, Процион. Про эти шесть звезд в главе 6 достоверно выяснено, что их групповая ошибка γ совпадает с величиной γstatZod A.
Вычислим для этих звезд величины Li(t, γstatZod A(t), φstatZod A(t)), то есть долготы этих звезд после компенсации соответствующей групповой ошибки на эпоху t. Разумеется, при этом можно совершить погрешность и, быть может, значительную. Причин, по крайней мере, две. Первая: параметр φ сильно влияет на значения долгот. В то же время, как мы видели, этот параметр определяется неустойчиво. Следовательно, нет никакой гарантии, что для всех шести звезд он один и тот же и равен φstatZod A. Вторая причина такова. Выше мы не изучали групповые долготные ошибки, которые также могут существовать, см. [1339]. Их анализ приводит к необходимости введения еще одной величины, параметризующей групповую ошибку. Можно взять параметр τ, см. главу 3. Это - угол поворота звездной сферы вокруг новых полюсов эклиптики, задаваемых параметрами γ и φ.
Обозначим Δ Li(t) = Li(t, γstatZod A(t), φstatZod A(t)) - li. Если изобразить поведение функции Δ Li(t), то она может быть представлена в виде суммы почти линейной функции (равномерное изменение долготы вследствие прецессии) и нерегулярной "добавки", отвечающей различного рода погрешностям. Поэтому, чтобы исключить из рассмотрения влияние прецессии, а также возможной систематической ошибки τ, введем величину
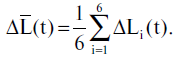
Величина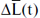 
достаточно точно измеряет изменение долгот рассматриваемых 6-ти звезд вследствие прецессии. Положим
Δ Li0(t) = Δ Li(t) - 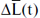. На величину Δ Li0(t) прецессия влияния уже практически не оказывает.
На рис.7.38
показаны изменения величин Δ Li0(t) как функций предполагаемой датировки t для шести рассматриваемых здесь звезд Альмагеста. Первое, что следует из рисунка, -- это малые скорости изменения величин Δ Li0(t) со временем. После компенсации прецессии "быстрые" звезды Альмагеста оказались очень "медленными" по долготам. Например, скорости изменения долгот Арктура и Регула почти равны друг другу. Самой быстрой звездой из шести становится Процион. Но его долгота за 3000 лет, -- от 1100 года до н.э. до 1900 года н.э., -- изменяется лишь на 17'. То есть чуть больше 5' за тысячу лет. Ясно, что такого медленного изменения долготы совершенно недостаточно для содержательной датировки.
На рис.7.39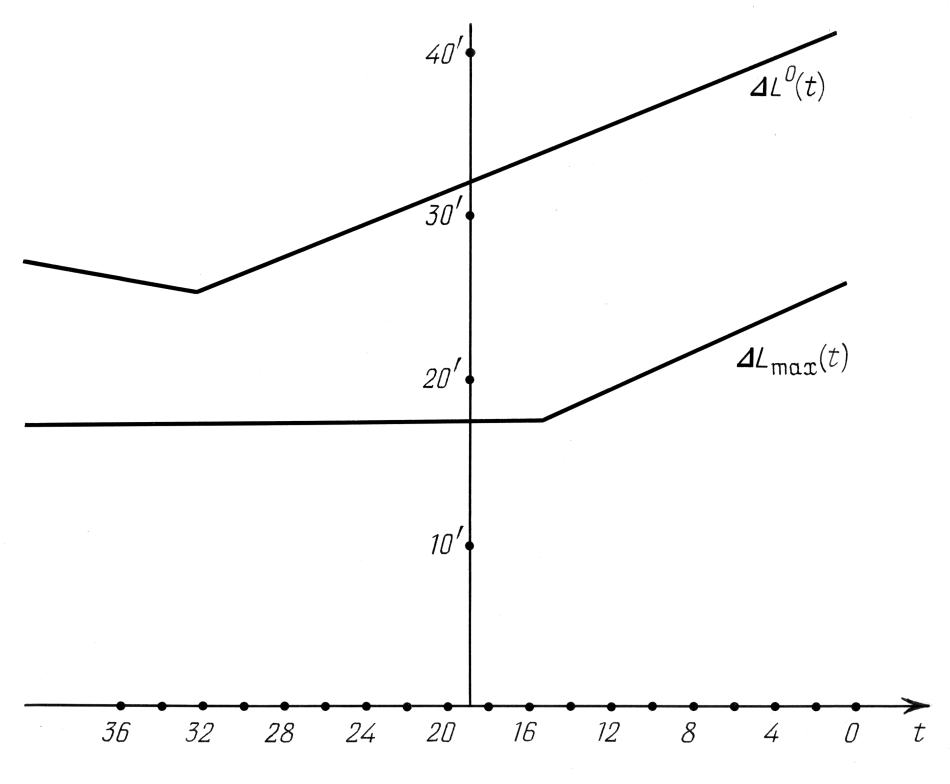
изображены два графика, которые в принципе могли бы служить для датировки. Однако поведение этих графиков говорит об их полной бесполезности в этом качестве. А именно, рассмотрим две функции:
Первая из них представляет собой максимальное по рассматриваемым звездам уклонение реальных долгот от долгот, записанных в Альмагесте. Уклонение берется по абсолютной величине, с учетом прецессии. Вторая функция, уже не зависящая от прецессии, -- это разность между максимальным и минимальным уклонениями. Функция Δ Lmax(t) достигает минимального значения при t=15, то есть в 400 году н.э., а функция Δ L0(t) -- при t=32,5, то есть около 2350 года до н.э. Обе функции принимают сравнительно большие значения, а именно, Δ L0(t) ≥ 25', а начиная со скалигеровской эпохи Гиппарха, Δ L0(t) ≥ 30'). Наконец, Δ Lmax(t) ≥ 17'. Все это говорит о том, что точность долгот слишком низка по сравнению со скоростями собственного движения. Мы не можем извлечь отсюда содержательное представление об истинной дате наблюдений.
Итак, вычисления подтвердили, что долготы каталога Альмагеста малоинформативны ввиду их низкой точности. По-видимому, причина этого правильно вскрыта Р.Ньютоном [614]. Он утверждал, что долготы в Альмагесте были кем-то подделаны, см. также главу 2. Сами мы подробных исследований в этом направлении не проводили. Вполне возможно, что при анализе долгот статистическими методами в их поведении также обнаружатся некоторые закономерности. Например, можно будет выявить в долготах отдельных частей каталога Альмагеста наличие групповых ошибок. Но, так это или нет, проведенные нами исследования показывают, что использовать долготы для уточнения датировки каталога Альмагеста, по-видимому, бессмысленно.
10. ПОВЕДЕНИЕ ДУГОВЫХ НЕВЯЗОК В КОНФИГУРАЦИИ, ОБРАЗОВАННОЙ ИНФОРМАТИВНЫМ ЯДРОМ АЛЬМАГЕСТА.
В главе 3 уже обсуждался вопрос о возможности датировки каталога путем сравнительного анализа двух конфигураций. Одна -- неподвижная, образованная звездами Альмагеста. Другая -- подвижная, образованная современными звездами. Было отмечено, что это сравнение можно провести вообще без ссылок на теорию Ньюкомба. Например, если рассматривать лишь разности дуговых расстояний в сравниваемых конфигурациях. Среди трудностей, препятствующих применению данного метода, были упомянуты следующие. Во-первых, -- возможные ошибки в отождествлениях звезд. Во-вторых, -- низкая точность измерений координат, приводящая к непомерно большим интервалам датировки. В третьих, -- невозможность, при таком подходе, разделить координаты на точно и неточно измеренные компоненты. Скажем, на широты и долготы.
Если выбрать в качестве исследуемой конфигурации информативное ядро каталога Альмагеста, то первые два препятствия снимаются. В самом деле, отождествление указанных звезд сомнений не вызывает, а точность их измерения в соответствии с нашей основной гипотезой должна быть высокой. Во всяком случае, это касается широт звезд. Кроме того, в состав информативного ядра входят две весьма быстро движущиеся звезды: Арктур и Процион. Разумеется, неизвестная нам неточность измерения долгот может привести к таким погрешностям датировки, которые невозможно оценить. Тем не менее, отсутствие необходимости оценивать групповые ошибки при таком подходе делает соответствующие вычисления интересными. Хотя оценить погрешности этих вычислений, к сожалению, не представляется возможным. По крайней мере -- на основе проведенных нами исследований.
Приведем здесь результаты наших вычислений в этом направлении, сделанных для уже рассматривавшихся выше конфигураций из 8 и 6 именных звезд Альмагеста.
Пусть lijA -- дуговое расстояние между i-й и j-й звездами Альмагеста. Пусть lijt -- аналогичное расстояние для "современных" звезд, рассчитанное для моментов наблюдения t=1, ..., 25. Обозначим через n число звезд в рассматриваемой конфигурации. Обозначим
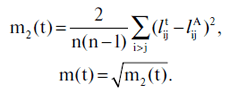
Величину m(t) можно рассматривать как обобщенное расстояние между конфигурацией, рассчитанной на эпоху t и соответствующей конфигурацией звезд Альмагеста. Точки минимума функций m2(t) и m(t) должны быть близки к дате составления каталога. На рис.7.40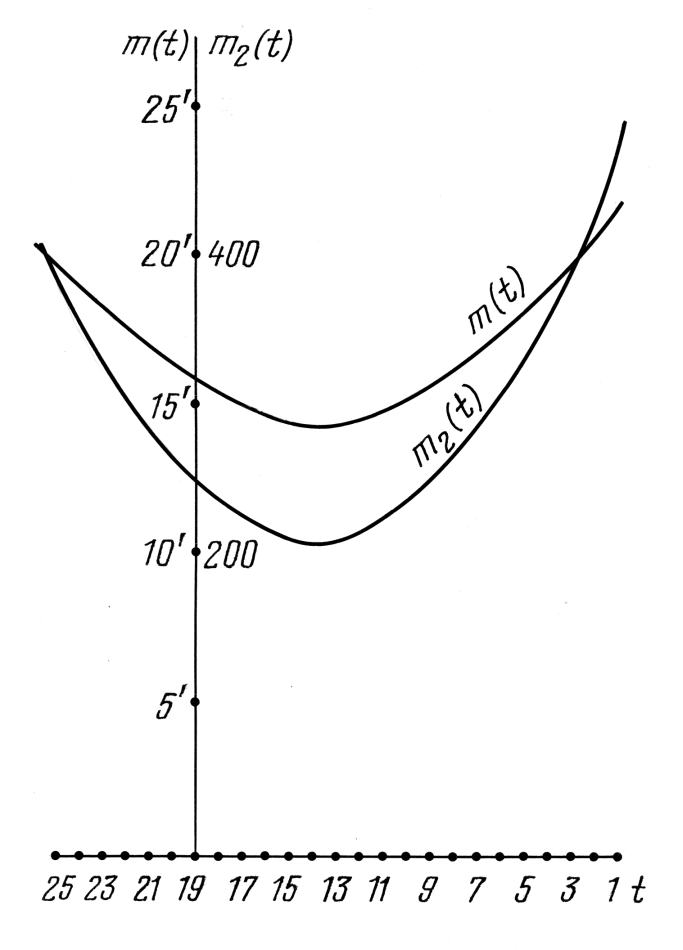
изображены графики функций m2(t) и m(t) для конфигурации из 8 именных звезд, а на рис.7.41
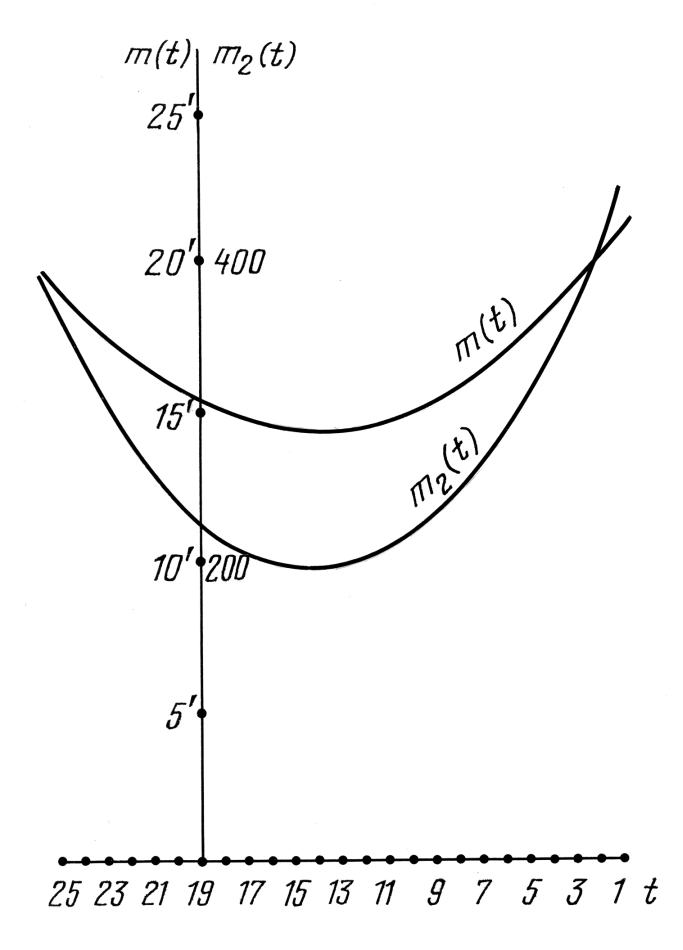-- для конфигурации из 6 именных звезд Альмагеста.
Видно, что в обоих случаях достаточно четкий минимум лежит в точке t=14 (500 год н.э.). При этом, минимум величины m(t) составляет около 14', что соответствует средней точности в 10' по каждой из координат. Ясно, что дата 500 год н.э. достаточно далеко отстоит от скалигеровской даты составления Альмагеста.
Некоторое "удревнение" полученной даты -- 500 год н.э. -- по сравнению с интервалом датировок, найденным выше с помощью анализа широт, объясняется тем, что ошибка по долготам, взятым отдельно от широт, принимает минимальное значение при t ≈ 31 (1200 год до н.э.). См. раздел 9. Конечно, датировка 1200 годом до н.э. для Альмагеста невозможна. Но все дело в том, что минимум средней невязки по долготам выражен очень слабо, поэтому точность этой датировки может составлять несколько тысяч лет. Другими словами, она ничему не противоречит, рис.7.38 и рис.7.39. Минимум же широтной невязки приходится на t=10, то есть на 900 год н.э., и выражен гораздо более ярко. В результате минимум дуговых среднеквадратичных отклонений оказывается в промежуточной точке t=14, то есть около 500 года н.э. Эта дата расположена гораздо ближе к точке более ярко выраженного минимума по широтам, чем к точке минимума по долготам.
11. ВЫВОДЫ.
1) Датировка каталога Альмагеста, получаемая предложенными нами статистической и геометрической процедурами, -- это интервал времени от 600 года н.э. до 1300 года н.э.
2) При датировке ранее, чем 600-м годом н.э. не существует способа совмещения реального неба и звездного атласа Альмагеста с менее чем 10-минутными широтными невязками для всех звезд информативного ядра Альмагеста.
3) Предположение о том, что точность каталога Альмагеста составляет не 10', а 15', все равно не приводит к включению скалигеровской эпохи Птолемея: I--II века н.э., в интервал возможных датировок.
4) Изменение состава информативного ядра Альмагеста также не приводит к расширению интервала датировки до скалигеровской эпохи Птолемея.
5) Реальные неточности в изготовлении астрономических приборов, приводящие к нелинейным искажениям звездного неба в каталоге, все равно не могут расширить или сдвинуть интервал датировки до скалигеровской эпохи Птолемея.
