BÖLÜM 5:
ESKİ OLAYLARIN TARİHLENMESİNDE MATEMATİKSEL İSTATİSTİK YÖNTEMLERİ
Kronolojinin analizindeki temel görev eski olayların tarihlenmesi için yeni bağımsız yöntemlerin geliştirilmesidir. Yalnızca bundan sonra, elde edilen sonuçları dikkate alarak kronolojiyi bir bütün olarak yeniden kurmak mümkündür. Tek tarz yöntemler -yukarıda tarif edilen astronomik yöntemler kadar etkin yöntemler bile- meselenin derin şekilde incelenmesi için yeterli değildir, çünkü tarihleme meselesi son derece zordur ve çeşitli yöntemler vasıtasıyla çapraz kontrolü gerektirmektedir. Çağdaş matematiksel istatistik eski vakayinamelerde anlatılan olayların tarihleme meselesine yeni bir yaklaşım sunmayı mümkün kılıyor. Bu bölümde, yazar ve çalışma arkadaşları tarafından geliştirilen yeni ampirik- istatistiksel yöntemler ve kronolojinin analizindeki bazı uygulamaları kısaca anlatılıyor.
Bu program şu şekilde uygulanmıştır:
1)Eski olayların tarihlenmesi için yeni ampirik-istatistiksel yöntemler geliştirilmiştir. Bu yöntemler bu kitabın yazarı tarafından şu yayınlarda sunulan birkaç istatistiksel ilke (model) temelinde geliştirilmiştir: [884], [885], [886], [888], [889], [890], [891], [895], [896], [897], [898], [899], [900], [901], [902], [903], [904], [905], [1129], [1130], [1131], [1132], [1135], [МЕТ1], [МЕТ2]. Ana yöntemler ve bunlara dayandırılmış modeller 1981 yılında 3. Vilnius Uluslararası Olasılıklar Kuramı ve Matematiksel İstatistik Konferansı’nda sunulan raporda formüle edilmiştir [885].
Sunulanlar şunlardı: Maksimumların korelasyonu ilkesi, küçük çarpıtmalar ilkesi (hükümdar hanedanları için), frekansların sönüm ilkesi, frekansların tekrarlama ilkesi, coğrafya haritalarının “iyileştirilmesi” ilkesi.
Bunların gelişimi 1985 yılında 4. Vilnius Uluslararası Olasılıklar Kuramı ve Matematiksel İstatistik Konferansı’nda [901] ve 1986 yılında Taşkent şehrinde düzenlenen Bernoulli Birinci Dünya Matematiksel İstatistik ve Olasılıklar Kuramı Derneği Kongresi’nde sunuldu. Daha sonra yeni ampirik-istatistiksel modeller A.T. Fomenko’nun, meslektaşları V.V. Kalaşnikov, G.V. Nosovskiy, S.T. Raçev ile birlikte yaptığı birtakım çalışmalarda sunulup deneysel olarak kontrol edildi: [357],[590], [591], [592], [593], [594], [595], [596], [597], [598], [600], [611], [723], [1140], [868].
2) Bu ilkeler ve modeller ile bunların etkinliği XVII-XX. yüzyılların pek geniş Orta Çağ ve Yeni Çağ tarih malzemeleri üzerinde denetlenmiştir. Bu denetleme, yöntemler vasıtasıyla elde edilen sonuçların doğruluğunu tasdik etmiştir.
3) Daha sonra aynı yöntemler en geç M.S. X-XVI. yüzyıllar ile tarihlenen Eski Çağ tarih malzemelerine uygulandı. Bkz. [884], [886], [887], [888], [891], [895], [897], [898], [900], [903], [905]. Burada ansızın, Eski Çağ ve Orta Çağ tarihinin Skaliger versiyonunda tuhaf “tekrarlamalar” ve “periyodisiteler” bulundu. Biz kolaylık sağlamak amacıyla bunları “hayalet suretler” olarak adlandırdık.
4) Bütün bu hayalet ikinci suretler yazarın makalelerinde [886], [888], [894], [896], [905] kısaca tasvir edilen küresel kronoloji haritası (KKH) olarak derlenip sıralandı. Önerilen yöntemlerin çok amaçlı, genel geçer yöntemler olduğunu düşünmüyoruz. Bütün bunların uygulanabilirlik sınırları açıkça belirtilmiştir, aşağıya bakınız. Elde edilen sonuçların doğruluğunun tek ölçütü yukarıda tasvir edilen astronomik tarihleme yöntemi dâhil olmak üzere çeşitli yöntemler vasıtasıyla bulunan tarihlerin uyuşmasıdır.
5) “Eski Çağ tarihi üzerine Skaliger ders kitabı” olan küresel kronoloji haritası yardımıyla Eski Çağ ve Orta Çağ kronolojisinin Skaliger versiyonunun oluşmasının varsayımsal mekanizmasını yeniden kurabildik. Bazı yöntemlerin özetini kısaca anlatalım.
1. LOKAL MAKSİMUMLAR İLKESİ
1.1.Tarihi Metnin Hacim Fonksiyonu
Maksimumlarım korelasyonu ilkesi ve bu ilkeye dayandırılan yöntem yazar tarafından geliştirilip [884], [885], [888], [1129]’da sunulmuştur.
Farz edelim ki, bir X tarih metnini, örneğin, bir A senesinden bir B senesine kadar uzanan genişçe zaman aralığında yer alan bilmediğimiz olayları anlatan bir vakayiname bulduk. Üstüne üstlük, bu seneler bilmediğimiz bir kronoloji sistemine göre yazılmış olabilir. Bundan sonra bu zaman aralığını (A,B) olarak işaretleyeceğiz. Tipik durum şudur: Vakayinamede betimlenen gelişmelerin tarihleri, yerel öneme sahip bir olaya göre hesaplanır. Örnek olarak bir şehrin kuruluşuna ya da şu ya da bu hükümdarın tahta çıkmasına göre vs. Böyle durumlarda, gelişmelerin tarihlenmesinin İZAFİ kronolojide verilmiş olduğunu söyleyeceğiz. Bu terim olayların bu şekildeki tarihlerini M.S. ya da M.Ö. terimleriyle ifade edilen MUTLAK tarihlerden ayırmamızı mümkün kılar. Eski bir belgede betimlenen olayların mutlak tarihleri nasıl yeniden kurulabilir? diye doğal bir soru ortaya çıkıyor. Mesela bir şehrin kuruluşunun bizi ilgilendiren olaylarının sayıldığı Jülyen tarihi nasıl hesaplanabilir?
Elbette bazı betimlenmiş olayları diğer tarihlenmiş vakayinamelerden biliyorsak, bu olayları çağdaş zaman skalasına bağlayabiliriz. Ama böyle bir özdeşleştirme çıkmıyorsa, tarihleme karmaşıklaşıyor. Bunun yanı sıra, bulunan vakayinamelerde betimlenmiş olayları fiilen biliyor olsak bile, görünürde bu olayların tasviri yine de tanınmıyor olabilir, çünkü bu vakayiname yabancı dilde yazılmıştır. Bunu yazan da bambaşka isimleri, lakapları, coğrafi isimleri kullanmış olabilir. Bu nedenle, olayların, incelenen metnin formel nicel özellikleri temelinde, tarihlenmesine yardım eden ampirik-istatistiksel yöntemlere sahip olmakta fayda var.
Farz edelim ki, X tarihî metni, her biri nispeten kısa – t numarasıyla bir senelik (ya da on senelik)- bir zaman aralığını betimleyen X(t) parçalarına bölünüyor. Bu tür metinlerin örneği çoktur. Mesela gelişmeleri sene sene anlatan vakayinameler, günlükler, birçok tarihî eser, ders kitapları ve tarih üzerine monografiler bu örneklerdendir. X(t) fragmanlarını, parçalarını, kolaylık sağlamak amacıyla, “bölüm” olarak adlandıracağız. Doğal olarak bu parçalar, söz konusu vakayinamenin iç izafi kronolojisi uyarınca kronoloji sırasına giriyor. Her biri ayrı bir seneyi tasvir eden “bölümler”e dayanan bu tarz bölümlendirme birçok tarihî metinde belirli biçimde bulunmaktadır. Örnek olarak meşhur Radzivilovskaya vakayinamesi (Geçmiş Zamanın Vakayinamesi) [715] dâhil olmak üzere birçok Rus vakayinamesi [671], [672], bu tarzdadır. Meşhur Roma kitabı Liber Pontificalis de aynı tarzdadır. (T. Mommsen, "Gestorum Pontificum Romanorum" Yayınevi, 1898).
X vakayinamesinin t senesinden aktardığı bilginin hacminin çeşitli nitelikleri mesela şöyle ölçülebilir:
1) vol X(t)= X(t) “bölümündeki” sayfa sayısıdır. Bu sayıyı X(t) “bölümünün” hacmi olarak adlandıralım. t senesi X vakayinamesinde hiç betimlenmemişse, hacim sıfıra eşit olabilir. Sayfaların sayısının yerine satırların, harflerin vs. sayısını saymak mümkündür. Bu durum yöntemin ana fikrini veya uygulamasını değiştirmiyor.
2) X vakayinamesinde t senesinden bahsedilme sayısı.
3) X(t) “bölümünde” anılan bütün tarihî şahsiyetlerin isimlerinin sayısı.
4) X(t) “bölümünde” somut bir isimden (şahıstan) bahsedilme sayısı.
5) X(t) “bölümünde” bir başka metne atıfların sayısı.
Bu tarz nicel özelliklerin hazinesi gayet büyük ve önemlidir. Bu özellikler vakayinamede tarif edilen her t senesine belli bir sayı atamaktadır. Genel olarak, farklı yıllara farklı sayılar uyacaktır. Bunun için, X(t) “bölümlerinin” hacimleri aslında t (senesinin) sayısının değişmesiyle birlikte değişecektir. X(A),...,X(B) hacimlerinin sırasını bu senelik X metninin HACİM FONKSİYONU (ya da HACİM GRAFİĞİ) olarak adlandıracağız.
1.2.Maksimumların Korelasyonu İlkesi
Bu suretle, bir G devletinin tarihinde A senesinden B senesine kadar olan bir tarih döneminin, senelik bir X vakayinamesinde yeterince geniş şekilde betimlenmiş olduğunu varsayalım. Yani X vakayinamesi, her biri ayrı bir seneyi betimleyen X(t) “bölümleri”ne bölünmüş ya da bölünebilir durumdadır. Bu parçaların her birinin hacimlerini sayalım. Mesela, sözcüklerin ya da harflerin, sayfaların vs. miktarını bulalım. Daha sonra elde edilen sayıları, yatay eksene t senelerini, düşey eksene “bölümlerin” hacimlerini, yani vol X(t), koyarak grafik suretiyle gösterelim, res.5.1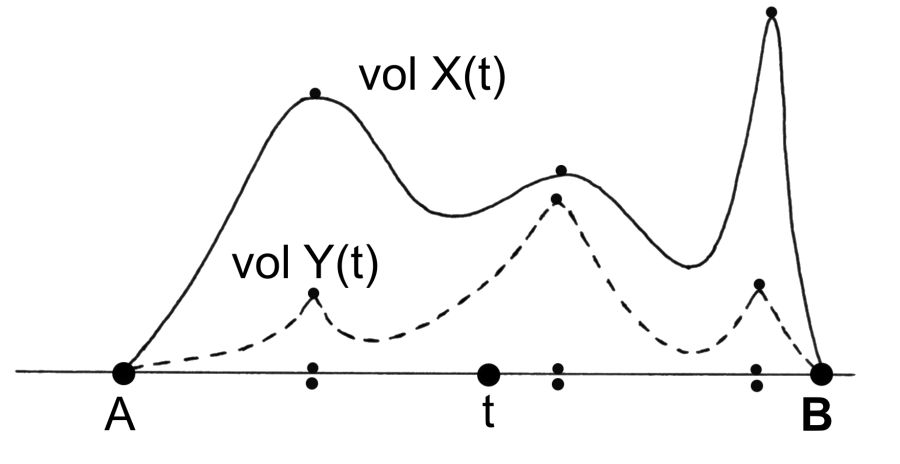
. Böylelikle bu X vakayinamesinin hacim fonksiyonunu göstermiş oluruz.
Aynı döneme (A,B) ait olup “olaylar akımını” sene sene gösteren başka bir senelik Y vakayinamesi için hacim fonksiyonu grafiği başka biçimde görünecektir, res. 5.1. Mesele şudur ki, X ve Y yazarlarının şahsi çıkarları hacimlerin dağılımında büyük önem taşıyor. Mesela, sanat tarihi üzerine X vakayinamesi ve askeri Y vakayinamesi bilginin hacminin dağılımını senelere epeyce farklı üleştiriyor. Örneğin, “yenilen” tarafın X vakanüvisi ordusunun yenilgisini pek zayıf ve ölçülü bir şekilde, birkaç kelime ile gösteriyor. Tersine, “yenen” tarafın Y vakanüvisi aynı savaştan ayrıntılı, coşkulu şekilde ve çok sayıda kelime ile bahsediyor.
Bu farklılıklar ne kadar mühimdir? Zaman aralığı, G devletinin tarihi ile belirlenen ve bu zaman aralığını ve bu devleti kesin bir şekilde tasvir eden tüm ya da hemen hemen tüm vakayinameleri niteleyen grafik nitelikleri var mı?
Grafiğin fırlayıp lokal maksimumlara ulaştığı t seneleri vol X(t) hacim grafiğinin önemli niteliğidir. Grafiğin bir t noktasında fırlaması bu senenin vakayinamede daha detaylı şekilde tarif edilmiş olması demektir. Mesela diğer senelere göre daha çok sayfada tarif edilmesi. O halde grafiğin fırlamaları, yani onun lokal maksimumları bize vakanüvis tarafından (A,B) zaman aralığında detaylı şekilde tarif edilen seneleri gösteriyor. Farklı X ve Y vakayinamelerinde farklı seneler detaylı şekilde tarif edilmiş olabilir.
Senelerin tariflerindeki bu eşitsizlik nasıl açıklanıyor? Açıklamalardan birisi şudur: Vakanüvis bu “eski seneyi” daha detaylı tarif etmiş, çünkü bu “eski seneden” kendisine korunmuş halde kalan daha çok bilgi ulaşmıştır. Mesela, ardışık senelere göre eski belgelerin hacminin daha büyük olması gibi.
Sonraki akıl yürütmemizin seyri şu şekildedir:
1) (A,B) Zaman aralığının hangi senelerinin, tasvir ettiği olayların çağdaşı olmayan sonraki vakanüvisler tarafından detaylıca yazılacağını önceden kestirmeyi mümkün kılan teorik modeli, yani istatistiksel varsayımı formüle edeceğiz.
2) Sonra bu istatistiksel modeli, yani varsayımı, matematiksel olarak anlatacağız.
3) XVI-XX. yüzyıllardaki geniş tarihî malzemeler üzerinde doğruluğunu denetleyeceğiz.
4) Teorik modelin bilgisayar deneyinde doğrulandığını keşfederek eski olayların tarihlenme yöntemlerini sunacağız.
Diyelim ki, С(t), t senesi hakkında çağdaşları tarafından yazılan bütün metinlerin hacmidir,
res. 5.2
. Yukarıdaki gibi, (A,B) zaman aralığında sayısal hacim grafiğini kuralım. Elbette С(t) grafiğinin kesin halini bugün bilemiyoruz. Mesele şudur ki, t senesinin çağdaşları tarafından yazılmış olan orijinal metinler gün geçtikçe kayboluyor. Günümüze kadar bunların yalnız bir kısmı ulaştı. С(t) grafiğini ORİJİNAL BİLGİ FONU GRAFİĞİ olarak adlandırabiliriz. Farz edelim ki, (A,B) devrinin çağdaşları bazı seneleri daha detaylı tasvir etmiş, yani bu senelerle ilgili daha çok bilgi kaydetmiş olsunlar. Böyle bir “orijinal eşitsizliğin” sebeplerini burada konuşmayacağız, çünkü bizim için bunlar bu aşamada önemli değil. С(t) hacim grafiğinin dilinde, “çağdaşları tarafından detaylı olarak tarif edilen” bu seneler, hacim grafiğinde fırlamalar ile belirecek.
Bir soru: С(t) grafiğinin sapmasına ve yüksekliğinin gittikçe azalmasına yol açan yazılı bilginin kaybedilip unutulmasının mekanizması nedir? BİLGİ KAYBI MODELİNİ formüle edelim.
С(t) grafiğinin yüksekliği gittikçe azaldığı halde, ÇAĞDAŞLARININ EN ÇOK METİN YAZDIĞI SENELERDEN DAHA ÇOK BİLGİ KALACAKTIR.
Bu modelin yeniden formüle edilmesi için şunu yapmakta fayda var. M zaman ânını B noktasının sağına kaydediyoruz,
res.5.2, ve M ânına kadar ulaşan ve (A,B) tarih döneminde bulunan t senesinin olaylarını anlatan metinlerin hacmini gösteren CM(t) grafiğini kuruyoruz.
Başka bir deyişle, CM(t) sayısı, M senesindeki “fonun gözlem ânına” kadar korunan t senesine ait orijinal eski metinlerin hacmini gösteriyor. CM(t) grafiği, kolaylık sağlamak amacıyla, (A,B) devrinin M senesine kadar korunmuş “kalan bilgi fonu” olarak adlandırılabilir. Şimdi modelimiz şu şekilde yeniden formüle edilebilir.
CM(t) KALAN BİLGİ FONUNUN HACİM GRAFİĞİNİN VE C(t) ORİJİNAL BİLGİ FONUNUN BİRİNCİL GRAFİĞİNİN FIRLAMALARININ (A,B) ZAMAN ARALIĞINDA AŞAĞI YUKARI AYNI SENELERDE OLMASI LAZIMDIR.
Elbette bu biçimdeki bir modeli sınamak güç, çünkü orijinal bilgi fonunun C(t) grafiğini bugün tam olarak bilmiyoruz. Ama teorik modelin sonuçlarının birini sınamak yine de mümkündür.
Aynı (A,B) tarih dönemini ve aynı “olaylar akımını” anlatan daha sonraki X ve Y vakanüvisleri bu eski dönemlerin çağdaşı olmadığı için, kendilerine ulaşan aşağı yukarı aynı metin kümelerine dayanmak zorundadırlar. Böylece daha çok metnin kaldığı seneleri “ortalama” olarak daha ayrıntılı ve daha az bilginin kaldığı seneleri “ortalama” olarak daha az ayrıntı ile tasvir edeceklerdir. Başka bir ifadeyle, vakanüvisler kendilerine daha çok eski metnin ulaştığı seneleri anlatırken anlatımın ayrıntı seviyesini artırmalıdırlar.
Hacim grafiklerinin dilinde bu model şöyle görünüyor. X vakanüvisi M devrinde yaşıyorsa CM(t) kalan bilgi fonuna dayanacak. Bir başka Y vakanüvisi M devrinden aslında farklı olan N devrinde yaşıyorsa CN(t) kalan bilgi fonuna dayanacaktır. Bkz.
res.5.3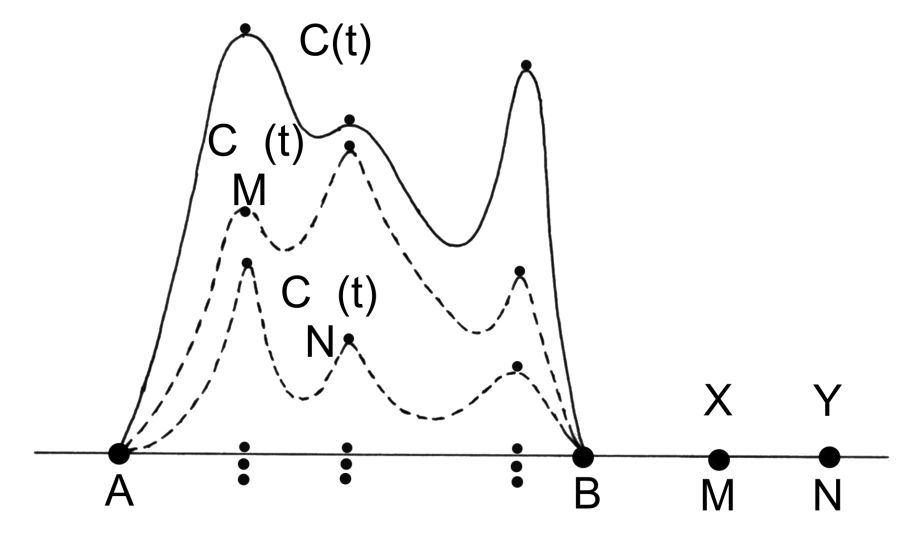
.
X ve Y vakanüvisinin “ortalama” olarak belli bir vazifeşinaslıkla çalışmış olduğunu beklemek doğaldır. Bu yüzden, (kendileri için) eski (A,B) döneminin kendilerine en çok bilginin, eski metnin ulaştığı senelerini daha detaylı anlatıyorlar.
Bir başka deyişle, vol X(t) hacim grafiği, CM(t) grafiğine göre yaklaşık olarak aynı senelerde fırlayacak. Aynı zamanda vol Y(t) grafiği, CN(t) grafiğine göre aynı senelerde fırlayacak,
res.5.3.
Ama CM(t) kalan bilgi fonu grafiğinin fırlama noktaları orijinal, birincil C(t) grafiğinin fırlama noktalarına yakındır. Benzer biçimde CN(t) kalan bilgi fonu grafiğinin fırlama noktaları birincil C(t) grafiğinin fırlama noktalarına yakındır. Buna göre, X ve Y vakayinamelerinin hacim grafikleri, yani vol X(t) ve vol Y(t) grafikleri aşağı yukarı aynı zamanda, zaman ekseninde “aynı” noktalarda fırlamalıdır. Başka bir deyişle, bunların lokal maksimum noktalarının belirgin şekilde birbirine yakın olması ve iyi uyuşması gerekir,
res.5.1.
Bu arada, vol X(t) ve vol Y(t) grafiklerinin genlikleri çok farklı olabilir,
res.5.4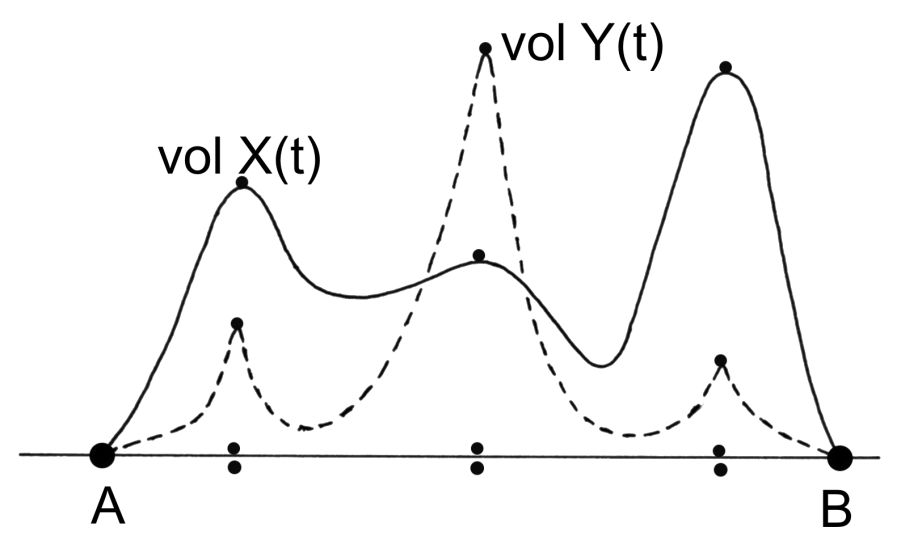
. Bunun yukarıda sayılan fikirleri etkilemediği ortadadır.
Nihai olarak maksimumların korelasyonu ilkesinin ifadesi şudur. Önceki fikirler yalnız yol gösterici olarak algılanabilir.
Maksimumların Korelasyonu İlkesi:
a) X ve Y vakayinameleri (metinleri) AÇIKÇA BAĞIMLI ise -yani aynı G devletinin (A,B) tarihî dönemindeki aynı “olaylar akımını” anlatıyorsa– X ve Y vakayinamelerinin hacim grafikleri (A,B) aralığında AYNI ZAMANDA LOKAL MAKSİMUMLARA ULAŞMALI (fırlamalı). Bir başka ifadeyle, “X vakayinamesinde detaylı şekilde anlatılmış” seneler ve “Y vakayinamesinde detaylı şekilde anlatılmış” seneler birbirine yakın olmalı ya da kesişmeli,
res.5.4.
b) Tersine, X ve Y vakayinameleri AÇIKÇA BAĞIMSIZ ise, yani ya (А,В) ve (C,D) farklı tarih dönemlerini ya da farklı devletlerdeki “olaylar akımını” anlatıyor ise, X ve Y vakayinamelerinin hacim grafikleri lokal maksimumlara FARKLI NOKTALARDA ulaşır. Başka bir ifadeyle, vol X(t) ve vol Y(t) grafiklerinin fırlama noktaları birbirine yakın olmamalı ve uyuşmamalı,
res.5.5
. Bu arada, iki grafiği kıyaslamak için önce (А,В) ve (C,D)’nin aynı boydaki kısımlarını birleştirmeliyiz.
Ne açıkça bağımlı ne de açıkça bağımsız olan diğer metin çiftlerini kolaylık sağlamak amacıyla YANSIZ olarak adlandıralım. Bunlar hakkında iddiada bulunmayacağız.
Bu ilke yeterince geniş, bağımlı, yani aynı “olaylar akımını” anlatan gerçek X ve Y vakayiname çiftlerinin hacim grafikleri aşağı yukarı aynı zamanda, aynı senelerde fırlıyorsa doğrulanacaktır. Öte yandan, BU FIRLAMALARIN YÜKSEKLİĞİ EPEYCE FARKLI OLABİLİR.
Tersine, gerçek bağımsız vakayinamelerin fırlama noktaları kesişmemelidir. Elbette somut bağımlı vakayinameler için hacim grafiğinin fırlamasının zamandaşlığı yalnızca yaklaşık olabilir.
1.3.İstatistiksel Model
Kabaca, fikir şudur: Fırlama noktalarının yakınlığını nicel olarak değerlendirmek için şunu yapacağız. Diyelim ki, iki vakayinamenin hacim grafiklerinin lokal maksimumlarının sayısı aynı. f[k] sayılarının karelerinin toplamı olan f(Х,Y) sayısını bulalım (f[k], sene katsayısında, X hacim grafiğinin k numaralı fırlama noktasından Y hacim grafiğinin k numaralı fırlama noktasına kadar olan uzaklıktır). İki grafik aynı zamanda fırlıyorsa, aynı numaralı fırlama noktaları kesişir ve bütün f[k] sayıları sıfıra eşit olur. Çeşitli gerçek H metinlerinin gayet büyük devinimsiz hazinesini ele alarak, her biri için f(Х,Н) sayısını hesaplayıp bu sayının f(Х,Y) sayısını aşamadığı H metinlerini seçelim. H metinlerinin bütün hazinesinde bu şekildeki metinlerin payını hesap ederek р(Х,Y) olasılığı olarak (rastlantısal H vektörünün düzenli dağılımı varsayımıyla) yorumlanabilen katsayıyı elde etmiş oluyoruz [904], [908], [1137], [884]. p(X,Y) katsayısı küçük ise, X ve Y vakayinameleri bağımlıdır, yani yaklaşık olarak aynı “olaylar akımını” anlatıyor demektir. Bu katsayı büyükse, X ve Y vakayinameleri bağımsızdır, yani farklı “olaylar akımından” haber veriyor demektir.
İstatistiksel modelin daha detaylı açıklamasına geçelim. Gerçek hacim grafiklerinin fırlamalarının zamandaşlığı yalnızca yaklaşık olabilir. Matematiksel istatistik yöntemi, iki grafiğin fırlamalarının ne kadar eşzamanlı olduğunu değerlendirmek için X ve Y vakayinamelerinde detaylı olarak anlatılan senelerin kesişmemesini ölçen bir p(X,Y) sayısını bulmayı mümkün kılıyor. Anlaşılacağı gibi, iki grafiğin fırlamalarının yakınlığını rastlantısal bir olay olarak inceliyorsak, p(X,Y) sayısını bu olayın olasılığı olarak algılayabiliriz (aslında bu durum yöntem için zorunlu değildir). Bu sayı ne kadar küçükse X’te detaylı şekilde anlatılan seneler, Y’de detaylı şekilde anlatılan senelerle o kadar iyi uyuşuyor. p(X,Y) katsayısının matematiksel açıklamasını verelim.
(A,B) zaman aralığını ve m1,..., mn-1 noktalarında lokal maksimumlara ulaşan vol X(t) hacim grafiğini inceleyelim. Kolaylık sağlamak için, her lokal maksimumun (fırlamanın) tek bir noktada bulunduğunu kabul edelim. Bu mi noktaları, yani seneler (A,B) zaman aralığını aslında farklı boydaki kısımlara bölüyor,
res.5.6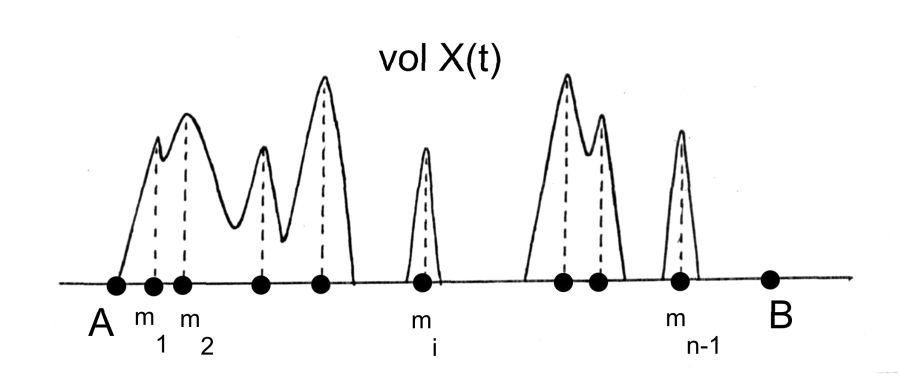
. Elde edilen kısımları senelerle ölçerek, yani bitişik lokal mi ve mi+1 maksimum noktaları arasındaki uzaklığı ölçerek a(X)=(x1,...,xn) tamsayı dizisini elde ediyoruz. Yani X1 sayısı A noktasından ilk lokal maksimuma kadar olan uzaklıktır. X2 sayısı ilk lokal maksimumdan ikincisine kadar olan uzaklıktır. Ve benzeri. Xn sayısı son lokal mn-1 maksimumundan B noktasına kadar olan uzaklıktır.
Bu diziyi n boyutlu Rn Öklid uzayında a(X) vektörüyle göstermek mümkündür. Örnek olarak, iki lokal maksimum olduğu durumda, yani n=3 ise, üç boyutlu uzayda tamsayısal a(X)=(x1,x2,x3) vektörünü elde ediyoruz. a(X)=(x1,x2,x3) vektörünü X vakayinamesinin LOKAL MAKSİMUMLAR VEKTÖRÜ olarak adlandıralım.
Bir başka Y vakayinamesi için bir başka a(Y)=(y1,y2,y3) vektörünü elde edeceğiz. Farz edelim ki, Y vakayinamesi uzunluğu (A,B) zaman aralığının uzunluğuna eşit olan (yani B- A=D-C) (C,D) zaman aralığındaki olayları anlatıyor. X ve Y vakayinamelerinin hacim grafiklerini karşılaştırmak için önce aynı uzunluktaki (A,B) ve (C,D) zaman aralıklarını birleştirelim. Elbette vol X(t) ve vol Y(t) grafiklerinin lokal maksimumlarının sayısı farklı olabilir. Ama maksimumlarının sayısının aynı olduğunu kabul edebiliriz ve bu nedenle karşılaştırılan X ve Y vakayinamelerinin a(X) ve a(Y) vektörleri aynı koordinat sayısına sahip olacaktır. Karşılaştırılan iki grafiğin maksimumlarının sayısı farklı ise şu yapılabilir. Bazı maksimumları kat kabul edelim, yani bu noktada birkaç maksimumun birleştiğini düşünelim. Bu kat maksimumların karşılığı olan kısımların uzunluklarının sıfıra eşit olduğu düşünülebilir. Bu iddiadan faydalanarak, X ve Y vakayinamelerinin hacim grafiklerinin lokal maksimumlarının sayısını açıkça eşitleyebiliriz. Elbette kat maksimumların kullanılması işlemi pek anlamlı değildir. Kat maksimumların kullanılmasının herhangi bir seçeneğini kaydedelim. Daha sonra kat maksimumların kullanılmasının bütün mümkün olan seçenekleri üzerinde bize gereken yakınlık katsayılarını azaltıp sözü geçen belirsizlikten kurtulacağız. Vurgulayalım ki, kat maksimumların kullanılması a(X) vektörünün bazı yerlerinde sıfır öğelerin, yani sıfır uzunluktaki kısımların çıkması demektir.
Böylelikle X ve Y vakayinamelerini karşılaştırarak a(X)=(x1,...,xn) ve a(Y)=(y1,...,yn) vektörlerinin, aynı koordinat sayısına sahip oldukları için, aynı Rn Öklid uzayında yer aldığını varsayabiliriz. Vurgulayalım ki, bu vektörlerin koordinat toplamı aynıdır ve B-A=D-C’e, yani (A,B) zaman aralığının uzunluğuna eşittir. Böylelikle:
x1 + ... + xn = y1 + ... + yn = B-A.
Şimdi koordinatları olumsuz olmayan ve c1+...+cn toplamı B-A sayısına, yani (A,B)
zaman aralığının uzunluğuna eşit olan bütün tamsayısal c=(c1,...,cn) vektörlerinin kümesini inceleyelim. Bu vektörlerin kümesini S vasıtasıyla işaretleyelim. Geometrik olarak bu vektörleri şöyle gösterebiliriz. Diyelim ki, bütün bunlar koordinat başlangıç noktasından, yani Rn uzayının 0 noktasından çıkıyor. Bütün bu c=(c1,...,cn) vektörlerinin uçlarını inceleyelim. Bütün bunlar, Rn uzayında
c1 + ... + cn = B-A,
denklemiyle (burada bütün c1,...,cn koordinatları negatif olmayan reel sayılardır) belirlenen L “çok boyutlu simpleks”i üzerinde yer alıyor. S’nin kümesi geometrik olarak L simpleksindeki “tüm noktaların” kümesi, yani L’den tamsayısal koordinatları olan bütün noktaların kümesi olarak gösteriliyor.
Açıktır ki, X ve Y vakayinamelerinin a(X) ve a(Y) lokal maksimumlarının vektörlerinin uçları S kümesine aittir,
res. 5.7
Şimdi a(X)=(x1,...,xn) vektörünü kaydedip bütün c=(c1,...,cn) vektörlerini inceleyelim. Bunların koordinatları L simpleksine ait ve şu denkleme uygundur:
[(с1 - x1)2 + ... + (cn - xn)2] < [(y1 - x1)2 + ... + (yn - xn)2].
Bütün bu c=(c1,...,cn) vektörlerinin kümesini K vasıtasıyla işaretleyelim. Matematiksel olarak bu vektörler devinimsiz a(X) vektöründen, a(X) vektörü ile a(Y) vektörü arasındaki r(X,Y) uzunluğunu aşmayan uzunlukta olarak tarif ediliyor. Burada vektörlerden bahsederken uçlarını kastediyoruz. Hatırlatalım ki,
(y1 - x1)2 + ... + (yn - xn)2
sayısı a(X) ile a(Y) vektörleri arasındaki r(X,Y) uzunluğunun karesine eşittir. Bu yüzden, K kümesi L simpleksinin, merkezi a(X) noktası olan, r(X,Y) yarıçaplı, n boyutlu küresinin bir kısmıdır.
Şimdi K kümesinde ve L kümesinde kaç tane tamsayısal vektör olduğunu sayalım. Elde edeceğimiz sayıları m(K) ve m(L) olarak işaretleyelim. p'(X,Y) “Hazırlık” katsayısı olarak bu iki sayının şu oranını alalım:
| p'(X,Y) = | m(K) |
| m(L) |
+9
| p'(X,Y) = | K kümesindeki “tüm noktaların” miktarı |
| L kümesindeki “tüm noktaların” miktarı |
K kümesi L kümesinin yalnız bir kısmı olduğu için p'(X,Y) sayısı [0,1] diliminde bulunuyor.
a(X) ve a(Y) vektörleri kesişiyorsa, p'(X,Y)=0. Tersine, a(X) ve a(Y) vektörleri birbirinden uzaksa p'(X,Y) sayısı bire yakın ve bire eşit bile çıkabilir.
Burada enteresan olan ama sonraları için gerekli olmayan p'(X,Y) sayısının yorumunu kayda geçirelim. Varsayalım ki, c=(c1,...,cn) vektörü rastlantısal olarak S kümesinin bütün vektörlerinden geçiyor olsun, hem de aynı olasılıkla bu kümenin herhangi bir noktasında ortaya çıkabilir. Bu durumda, rastlantısal c=(c1,...,cn) vektörü S kümesinde, yani (n-1) boyutlu L simpleksinin tamsayılar kümesinde DÜZENLİ OLARAK dağılıyor denebilir. O zaman, bulduğumuz p'(X,Y) sayısı olasılıksal yoruma yol açıyor. O sayı, basitçe, rastlantısal c=(c1,...,cn) vektörünün devinimsiz a(X) vektöründen a(X) ve a(Y) vektörleri arasındaki uzunluğu aşmayan uzunlukta çıkmasından ibaret olan rastlantısal olayın olasılığına eşittir. Bu olasılık ne kadar azsa, gözlemlediğimiz a(X) ve a(Y) vektörlerinin yakınlığı da o kadar azdır. Bir başka deyişle, bu durumda bunların yakınlığı aralarında bir bağımlılık olduğunu gösteriyor. p'(X,Y) sayısı ne kadar azsa, bu bağımlılık o kadar kuvvetlidir.
Rastlantısal c=(c1,...,cn) vektörünün L simpleksindeki dağılımının düzenliliği, bu vektörün tarihî vakayinamelerin ya da incelenen (A,B) zaman aralığını anlatan benzeri metinlerin veya “bölümlerin” hacim fonksiyonunun bitişik lokal maksimumları arasındaki uzunluğu göstermesi ile gerekçelendirilebilir. Farklı tarihî devirlerde farklı devletlerden bahseden farklı vakayinameler incelenirken lokal maksimumun (A,B) zaman aralığının herhangi bir noktasında “eşit olasılıkla” çıkabileceğini düşünmek gayet doğaldır.
Yukarıda tarif edilen çizim vakayinamelerin hacim grafiklerinin kat maksimumlarının kullanımının bir seçeneğini kaydetmiş olduğumuz tahminiyle yapıldı. Elbette bu tarz seçenekler çoktur. Bütün bu seçenekleri ele alıp her birisi için p'(X,Y) sayısını alalım. Daha sonra da elde etmiş olduğumuz en küçük sayıyı seçelim. Onu p''(X,Y) olarak işaretleyelim. Yani biz, p'(X,Y) katsayısını vol X(t) ve vol Y(t) grafikleri için lokal maksimumların kullanımının bütün var olan seçeneklerinde azaltacağız.
Nihayet hatırlayalım ki, X ve Y vakayinamelerinin p''(X,Y) katsayısı alınırken X ve Y vakayinameleri eşitsiz durumda kalmıştı. Mesele şudur ki, yukarıda r(X,Y) yarıçaplı, merkezi a(X) noktasında bulunan n boyutlu küreyi inceledik. X ve Y vakayinameleri arasında çıkmış olan eşitsizliği ortadan kaldırmak amacıyla bunların yerlerini değiştirip tarif edilen çizimi tekrarlayalım, ancak yeni durumda n boyutlu kürenin merkezi a(Y) noktasında bulunacak. Sonuçta bir p''(Y,X) sayısı elde edeceğiz. Kesin p(X,Y) “simetrik katsayısı” olarak p''(X,Y) ve p''(Y,X) sayılarının aritmetik ortalamasını alacağız, yani:
| p(X,Y)= | p''(X,Y) + p''(Y,X) |
| 2 |
Görsellik sağlamak için, p'(X,Y) hazırlık katsayısının anlamını yalnız iki lokal maksimumlu hacim grafiğinde örnek olarak açıklayalım. Bu durumda,
a(X) = (x1, x2, x3) ve a(Y) = (y1, y2, y3)
vektörleri üç boyutlu Öklid uzayındaki vektörlerdir. Uçları, R3 uzayındaki koordinat ekseninden aynı B-A sayısını kesen iki boyutlu eşkenar L üçgeninde yatıyor. Bkz.
res.5.8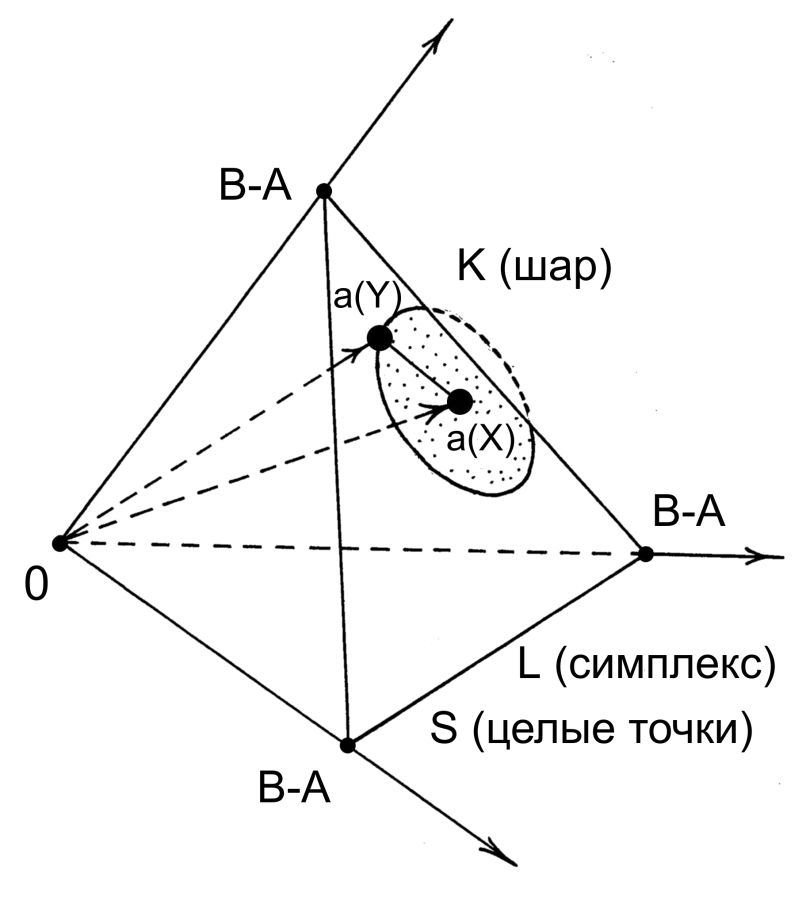
. a(X) noktasından a(Y) noktasına kadar olan uzunluğu |a(X)-a(Y)| olarak işaretlersek, K kümesi, L üçgeni ile merkezi a(X) noktasında bulunan ve yarıçapı |a(X)-a(Y)|’e eşit olan üç boyutlu kürenin kesişimidir. Bundan sonra, K kümesindeki ve L üçgenindeki “tamsayısal noktaların”, yani tamsayısal koordinatlı noktaların miktarını saymak gerek. Bulunan sayıların oranını alarak p'(X,Y) katsayısını elde edeceğiz.
Somut hesaplamalarda p'(X,Y) katsayısının hesaplanmasının yaklaşık (türetilmiş) seçeneğinden faydalanmak kullanışlıdır. Mesele şudur ki, K kümesinde tamsayısal noktaların hesaplanması gayet güçtür fakat ayrık (diskret) modelden aralıksız modele geçip bu güçlüğü yenmek mümkün görünüyor. İyi biliniyor ki, (n-1) boyutlu L simpleksindeki (n-1) boyutlu K kümesi gayet büyük ise K’deki tüm noktaların miktarı aşağı yukarı K kümesinin (n-1) boyutlu hacmine eşittir. Bunun için baştan itibaren p'(X,Y) hazırlık katsayısı olarak (n-1) boyutlu K hacminin (n-1) boyutlu L hacmine göre oranını, yani şunu kullanmak mümkündür:
| p'(X,Y)= | (n-1)-boyutlu K hacmi |
| (n-1)-boyutlu L hacmi |
Örneğin, iki lokal maksimum olduğunda p'(X,Y) katsayısı olarak şu oranı almak
gerekir:
| K kümesinin alanı --------------------------- |
| L üçgeninin alanı |
Elbette B-A değeri düşükse, “ayrık katsayı” ve “aralıksız katsayı” farklıdır. Ama bizim araştırmalarımızda B-A zaman aralığı onlarca ve hatta yüzlerce seneyi bile hesaplıyor, bu sebeple amaçlarımız için büyük bir hata yapmış olmadan, aralıksız p'(X,Y) modelini güvenle kullanabiliriz. “Aralıksız p'(X,Y) katsayısını” bulup yukarıdan ve aşağıdan değerlendirmek için net matematiksel formüller şu makalede bulunmaktadır, [884], s.107
Tarif edilen modeli bir daha açık ve kesin olarak belirtelim. Tarih metinlerinin somut grafikleri üzerinde çalışılırken rastlantısal küçük fırlamaları ortadan kaldırmak için grafikleri düzleştirmek gerek. Biz “komşulara göre ortalayarak”, yani her t noktasında hacim fonksiyonunun değerini fonksiyonun 3 noktasında, t-1, t, t+1 noktalarında aritmetik ortalamasının yerine geçirerek bunu yaptık. “Kesin p(X,Y) katsayısı” olarak böyle düzleştirilmiş grafikler için hesaplanmış değeri almak gerekmektedir.
X ve Y açıkça bağımlı metin çiftlerinin çoğunluğu için p(X,Y) katsayısı “küçük” ya da açıkça bağımsız metinler için p(X,Y) katsayısı tersine “büyük” çıkarsa yukarıda formüle edilmiş maksimumların korelasyonu ilkesi doğrulanacaktır.
1.4.Maksimumların Korelasyon İlkesinin Deneysel Testi. Bağımlı Ve Bağımsız Tarihî Metinlerin Örnekleri
1978-1985 yılları arasında yazar tarafından onlarca somut tarihî metin çifti için р(Х,Y) katsayısını hesaplamak amacıyla ilk kapsamlı deney yapıldı. Ayrıntılar için bkz. [904], [908], [1137], [884].
р(Х,Y) katsayısının gayet net bir şekilde açıkça bağımlı ve açıkça bağımsız metinler arasında ayrım yaptığı ortaya çıktı. Araştırdığımız bütün farklı tarihî dönemleri ve farklı devletleri tasvir eden, yani bağımsız gerçek X ve Y metin çiftleri için lokal maksimumların miktarı 10-15 ise, р(Х,Y) katsayısının 1 ila 1/100 arasında dalgalandığı keşfedildi. Aksine, tarihî X ve Y vakayinameleri açıkça bağımlı ise, yani aynı olayları anlatıyor ise, aynı maksimumların miktarı için р(Х,Y) katsayısı 10-8’i aşmıyor.
Böylelikle, bağımlı ve bağımsız metinlerin değerleri arasında birkaç büyüklük sırasını içeren kopma keşfediliyor. Vurgulayalım ki, önemli olan elde edilmiş katsayıların mutlak değerleri değil, “açıkça bağımlı metinler için katsayıların alanının” “açıkça bağımsız metinler için katsayıların alanından” birkaç büyüklük sırasıyla ayrılmasıdır. Tipik örnekler verelim. Özellikle enteresan vakayinamelerin hacim fonksiyonlarının net değerlerini kitabın sonundaki 2.Ek’te veriyoruz.
ÖRNEK 1. Res.5.9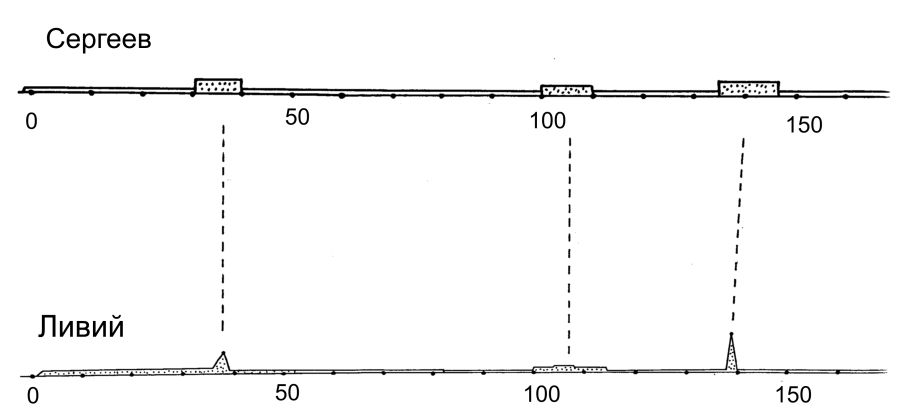
, рис.5.10
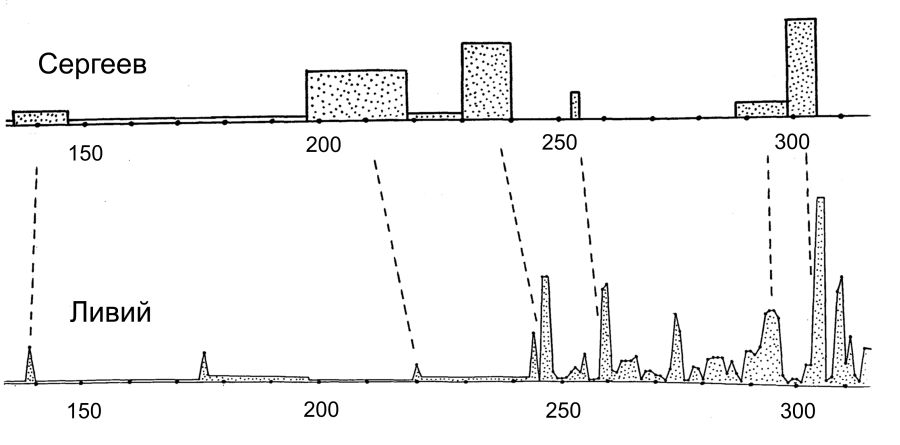, рис.5.11’de
açıkça bağımlı iki tarihî metnin hacim grafikleri gösterilmiştir.
X metni olarak, çağdaş yazar V.S. Sergeyev’in tarihî monografisi “Eski Roma’nın Tarihi Üzerine Denemeler” eserini (c.1-2, Moskova, 1938, OGİZ) aldık.
Y metni olarak, bir “antik” kaynağı, Titus Livius’un “Roma Tarihi” eserini (c.1-6, Moskova, 1897-1899) aldık.
Skaliger kronolojisine göre, bu metinler güya M.Ö. 757-287 senelerini anlatıyor. Böylece buradaki A = M.Ö. 757 senesi, B = M.Ö. 287 senesidir. Metinlerin ikisi de takriben aynı tarihî dönemi, aynı olayları anlatıyor. Apaçıktır ki, hacim grafiklerinin ana fırlamaları hemen hemen aynı zamanda yer alıyor. Fonksiyonların nicel karşılaştırması için önce grafiklerin ana, orijinal dalgalanmalarına yapışan “ufak dalgacıkları”, ikincil fırlamaları düzleştirmek gerek. p(X,Y) katsayısını hasaplarken miktarı onbeşi aşmayan ana lokal maksimumlarını bulabilmek için bu grafikleri düzleştirip ortaladık. Burada р(Х,Y) = 2X10-12 çıktığı görülmüştür. Katsayının küçük değeri karşılaştırılan metinlerin bağımlılığını gösteriyor. Bu durumda bu pek şaşırtıcı değil. Daha önce kaydettiğimiz gibi, iki metin “eski” Roma’nın aynı dönemini tarif ediyor. р(Х,Y) katsayısının küçük değeri gösteriyor ki, iki grafiğin fırlama noktalarının araştırılan yakınlığı rastlantısal olay olarak algılanacaksa, bu durumda bunun olasılığı son derece düşüktür. Gördüğümüz kadarıyla, çağdaş yazar V.S.
Sergeyev kitabında “antik” kaynağını çok titiz bir şekilde üretmiş. Tabii kendi fikir ve yorumlarıyla donatmış, ama anlaşıldığı gibi bu ekler metinlerin bağımlılığına hiç yansımıyor.
Şimdi Х' “vakayinamesi” olarak tekrar V.S. Sergeyev’in kitabını ve Y' “vakayinamesi” olarak metnindeki sene sırasını tersine geçirerek aynı kitabı alalım. Yani, Sergeyev’in kitabını arkadan öne doğru okumuş gibi yapalım. Bu durumda р(Х',Y') = 1/3 çıktığı görülüyor. Böylece karşılaştırılan metinlerin bağımsızlığını gösteren öncekine göre bire çok daha yakın bir değer elde ediyoruz. Bu da pek şaşırtıcı değildir, çünkü yaptığımız “vakayinamenin çevirme işlemi” iki açıkça bağımsız metin veriyor.
ÖRNEK 2. İki açıkça bağımlı tarihî metni, X – Nikiforovskaya vakayinamesi [672], Y – Supraslskaya vakayinamesi [672] olmak üzere iki Rus vakayinamesini alalım. İkisinde de aynı tarihî dönem, güya M.S. 850-1256 seneleri arası anlatılıyor.
Hacimlerinin grafikleri res.5.12’de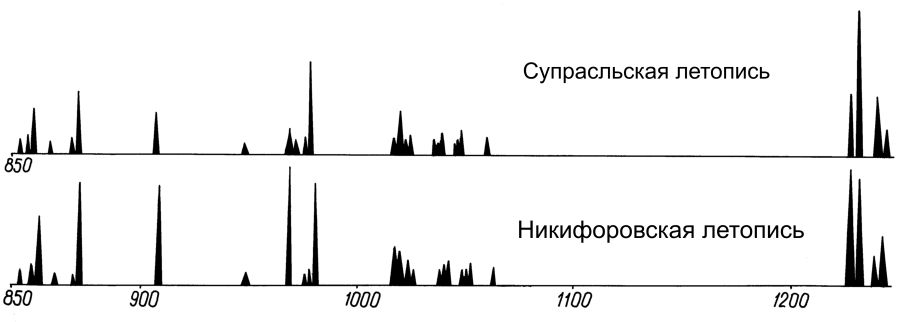
gösterilmiştir. “Bölümlerin” iki hacim grafiği 850-1256 senelerinin arasında hemen hemen aynı zamanda, aynı senelerde 31 fırlama yapıyor. Hesaplamaya göre р(Х,Y) = 10-24. Bu değer pek küçüktür, bu da bu metinlerin bağımlılığını ispatlıyor. 2. Ek’te bu vakayinamelerin hacim fonksiyonlarının net nicel değerlerini sunuyoruz.
ÖRNEK 3. Şu iki Rus vakayinamesini ele alalım: X – Holmogorovskaya vakayinamesi [672], Y – Geçmiş Yılların Vakayinamesi (Nestor Vakayinamesi).
İki vakayinamede de güya M.S. 850-1000 seneleri arası tanımlanmıştır. Vakayinamelerin hacim grafikleri de hemen hemen aynı zamanda lokal maksimumlara ulaşıyor. Yine bu durum da rastlantısal değil, doğaldır. Aksi halde 1015 ihtimalde bir ihtimal gerçekleşmiş olmalıdır. Burada p(X,Y)=10-15. Belirlenen zaman aralığında bu iki vakayiname bağımlıdır. Res.5.13’te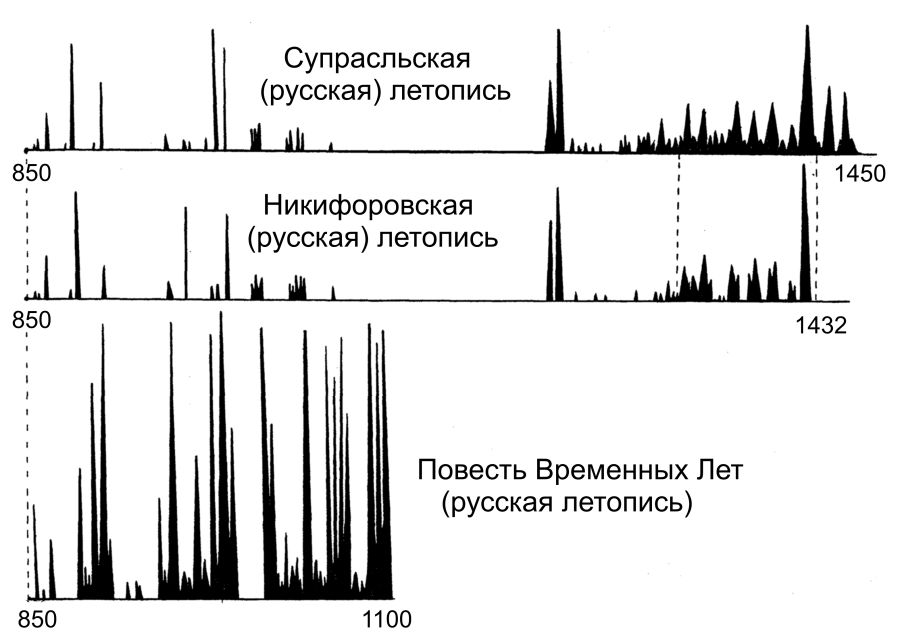
üç hacim grafiği gösterilmiştir: Bu grafikler Supralskaya, Nikiforskaya ve Nestor vakayinameleri içindir. Son vakayiname daha zengindir, bu yüzden grafiği daha çok lokal maksimuma sahiptir ve bağımlılığı o kadar ortada değildir. Ama grafik düzleştirildikten sonra bu üç grafik arasında belirgin bir bağımlılığın var olduğu ortaya çıkıyor. “Zengin” ve “yoksul” vakayinamelerin karşılaştırılması hakkındaki ayrıntıları “Tarihleri Değiştiriyoruz Her Şey Değişiyor” kitabının 3. bölümünde anlatıyoruz. Sözü geçen vakayinamelerin hacim dağılımı bu kitabın 2. Ek’inde bulunmaktadır.
ÖRNEK 4. Bu örnek Orta Çağ Roma tarihinden alınmıştır.
X – Alman tarihçisi Ferdinand Gregorovius’un “Orta Çağ Roma Şehrinin Tarihi” kitabı, c.1-6 [196]. Bu kitap çok sayıda Orta Çağ seküler ve dinsel belgesi temelinde XIX. yüzyılda yazılmıştır.
Y - Liber Pontificalis (T. Mommsen, Gestorum Pontificum Romanorum, 1898). Liber Pontificalis, yani Orta Çağ Roma Papalarının listesi ve yaşam öyküleri XIX. yüzyılda Teodor Mommsen tarafından Orta Çağ Roma metinleri temelinde yaratılmıştır. Buradaki p(X,Y)=10-10 değeri iki metnin belirgin bağımlılığını gösteriyor. Böyle bir yakınlığın rastlantısal olduğunun kabul edilmesi, 10 milyarda 1 ihtimalin gerçekleşmesi anlamına gelecektir.
Vesaire. Bütün incelediğimiz hem açıkça bağımlı hem de açıkça bağımsız onlarca tarihî metinde bizim teorik modelimiz doğrulanmıştır. Böylece bağımlı tarihî metinleri, yani aynı zaman dönemini, aynı devletin, bölgenin tarihindeki aynı “olaylar akımını” anlatan metinleri istatistiksel olarak nitelemeyi mümkün kılan bir eğilim keşfetmeyi başardık. Bunun yanı sıra, deneylerin gösterdiği gibi, iki tarihî X ve Y metni bağımsız ise, yani açıkça farklı tarihî dönemleri ya da farklı bölgeleri ya da çok farklı “olaylar akımını” anlatıyorsa, o zaman “olaylar akımı” grafikleri, vol X(t) ve vol Y(t) hacim grafikleri çok farklı senelerde fırlıyor. Yani aralarında hiç korelasyon gözlenmemekte. Bu son durumda p(X,Y) katsayısı için lokal maksimumların miktarı 10-15 ise tipik değer 1 ila 1/100 arasında dalgalanıyor. Tipik bir örnek verelim.
ÖRNEK 5. Tekrar Roma’nın “eski” tarihine dönelim. Karşılaştırılacak X ve Y metinleri olarak V.S. Sergeyev’in “Eski Roma’nın Tarihi Üzerine Denemeler” kitabından iki parçayı alalım [767]. Birincisi, güya M.Ö. 520-380 senelerini anlatan parça, öbürü ise güya M.Ö. 380-240 senelerini anlatan parça. Bu dönemlerin bağımsız olduğu kabul edilmektedir. Burada p(X,Y) katsayısı 1/5’e eşittir. Bu değer açıkça bağımlı lokal maksimumların benzer miktarı ile metinlerin tipik 10-12 - 10-6 değerlerinden çarpıcı biçimde farklıdır. Böylelikle bu iki metin, Sergeyev’in kitabının iki “yarısı”, gerçekten, bağımsız çıkıyor.
Yukarıda “bölümün” nicel özelliği olarak hacmini kullandık. Ama araştırmalarımızın gösterdiği gibi, gayet geniş tarihî metinler için benzer istatistiksel paralellikler diğer nicel özellikler kullanılırken de ortaya çıkıyor. Örnek olarak her “bölümde” ismin miktarı, diğer vakayinamelere atıfların sayısı vs. verilebilir.
Bizim bilgisayar deneyimizde, a) eski metinler eski metinler ile; b) eski metinler çağdaş metinler ile; c) çağdaş metinler birbirleriyle karşılaştırılmıştır.
Söylemiş olduğumuz gibi, “bölümün” hacim grafiklerinin yanı sıra metinlerin diğer nicel özellikleri de incelenmiştir. Mesela, kaydedilmiş isimlerin sayısının grafiği, metinde bir senenin anılma sayısının grafiği, bir başka devinimsiz metne atıfların sıklığının grafiği vs. [904], [908], [1137], [884].
Bütün bu nitelikler için maksimumların korelasyon ilkesinin geçerli çıktığı anlaşılmıştır. Yani, bağımlı metinlerin grafikleri hemen hemen aynı zamanda fırlama yapıyor ama bağımsız metinlerin fırlama noktaları birbirlerine yakın olmamakta ve hiç uymamaktadır.
Ana modelimiz olan istatistiksel varsayımdan bir sonuç daha çıkaralım.
Eğer iki tarihî metin açıkça bağımlı ise, yani aynı devlette aynı zaman aralığında aynı “olaylar akımını” anlatıyor ise, sözü geçen herhangi bir çift özellik için grafikler aşağı yukarı aynı senelerde fırlama yapıyor. Bir başka ifadeyle, iki vakayinamede bir sene bitişik senelere göre daha detaylı anlatılmış ise, iki vakayinamede bu senenin anılması sayısı, o senede anılan kişilerin isimlerinin sayısı vs. artacak. Aksine, metinler açıkça bağımsız ise, sözü geçen nicel özellikler arasında hiç korelasyon olmayacak.
“Maksimumların bu ikincil korelasyon ilkesinin” somut açıkça bağımlı tarihî metinler üzerinde sınanması bu ilkenin doğruluğunu ortaya koymuştur [884], s.110-111.
1.5.Tarihî Metinlerin Tarihlenmesi İçin Yöntemler
Teorik modelimiz büyük deneysel malzeme üzerinde doğrulandığından, eski olayların tarihlenmesi için yeni yöntemler sunabiliriz. Elbette bu model genel geçer değildir. Yöntemin ana fikrini betimleyelim.
Y, mutlak tarihleri kaybolan, bildiğimiz “olaylar akımını” anlatan belli bir tarihî metin olsun. t seneleri ise, metindeki tarihi bilinmeyen bir yerel olaydan, mesela bir şehrin kuruluşundan ya da bir çarın tahta çıkmasından itibaren sayılıyor olsun. Y metni için “bölümlerin” hacim grafiğini hesaplayıp, tarihlerini bildiğimiz olayların anlatıldığı diğer metinlerin hacim grafikleri ile kıyaslayalım. Bu metinler arasında р(Х,Y) katsayısı küçük olan – yani bağımlı metin çiftlerininki gibi aynı büyüklük sırasına sahip (örneğin lokal maksimumların uygun miktarı için 10-8 sayısını aşmayan) - X metni bulunursa, bu metinlerde anlatılan “olaylar akımının” yakınlığı ya da kesişmesi hakkındaki sonuca büyük ihtimalle varılabilir. Üstelik р(Х,Y) sayısı ne kadar küçükse bu olasılık o kadar büyüktür.
Bunun yanında, karşılaştırılan iki metin görünürde hiç benzemeyebilir. Örneğin, aynı kitabın farklı ülkelerde, farklı yazarlar tarafından, farklı dillerde yazılmış iki varyantı olabilir.
Bu yöntemler tarihleri bilinen Orta Çağ metinleri üzerinde deneysel olarak sınanmıştır.
Elde edilen tarihler bu tarihlerle uyuşmuştur. Tipik örnekler verelim.
ÖRNEK 6. Y metni olarak bir Rus vakayinamesini, 320 senelik zaman aralığındaki olayları anlatan Dvina vakanüvisinin kısa baskısı denilen eseri aldık [672]. Sunulan yöntemleri kullanarak vakayinamede anlatılan olayları tarihlemeyi deneyelim. “Rus vakayinamelerinin külliyatında” yayımlanan bütün vakayinameleri gözden geçirerek, vol X(t) hacim grafiğini, Y metninin vol Y(t) grafiğinin fırladığı senelerde fırlama yapan X metnini buluyoruz, res.5.14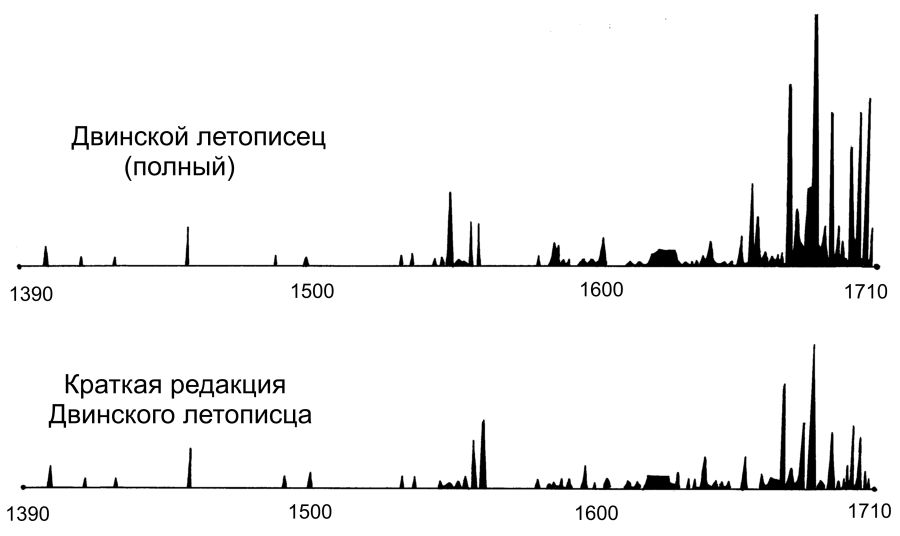
.
Grafikleri kıyaslayarak önce (А,В) ve (C,D) zaman aralıklarını birleştirip birbirinin üstüne koyuyoruz. Hesaplamaya göre burada р(Х,Y) = 2X10-25. Buna göre, bu iki vakayiname büyük ihtimalle aşağı yukarı aynı “olaylar akımını” anlatıyor. Böylece Y metninde betimlenen olayları, biçimsel olarak metinlerin yalnız istatistiksel niteliklerinin karşılaştırılması temelinde tarihlemeyi başardık. X vakayinamesinin Dvina vakanüvisinin uzun baskısı olduğu ortaya çıkıyor [672]. Bu vakayinamenin M.S. 1390-1707 senelerine ait olan “olaylar akımını” tasvir ettiği kabul edilmektedir. Sonuçta, X metninin elde ettiğimiz tarihinin standart tarihi ile uyuşması yöntemlerimizin etkinliğini ispatlıyor.
ÖRNEK 7. “Tarihi bilinmeyen Y metni” olarak Rus Akademik Vakayinamesi’ni alalım [672]. Yukarıda tarif edilen örneği takip ederek uzun zaman geçmeden X metnini buluyoruz. Bulunan metin de güya M.S. 1336-1374 senelerini betimleyen Supralskaya Vakayinamesi’nin bir kısmı. vol X(t) hacim grafiğinin de vol Y(t) hacim grafiğinin fırladığı senelerde fırlama yaptığı ortaya çıkıyor, res. 5.15.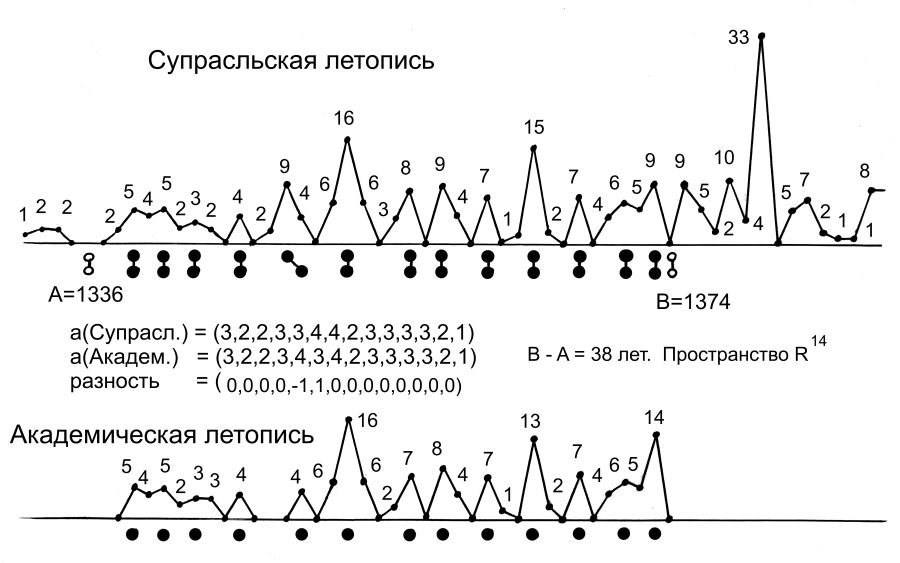
Hesaplamaya göre burada p(X,Y)=10-14. Katsayının değerinin bu kadar küçük olması bu iki metnin bağımlılığını gösteriyor. X vakayinamesi tarihlenmiş olduğu için Y vakayinamesini de tarihliyoruz. Y metninin elde ettiğimiz tarihi önceden bilinen tarihi ile uyuştu.
XV-XIX. yüzyıllardaki benzer onlarca metni ele aldık. Bütün durumlarda, bilinmeyen Y metninin elde ettiğimiz tarihi alışılmış tarihi ile uyuşmuştur.
Elbette son sayılan örneklerde yeni bir şey öğrenmedik, çünkü mesela Dvina vakanüvisi’nin kısa baskısı önceden biliniyordu ve doğruluğundan şüphe etmek için sebebimiz yoktu, çünkü bu eser kronoloji açısından nispeten sağlam bir dönem olan XIV- XVIII. yüzyıllara aittir. Ama uzun zaman geçmeden, yöntemlerimizin geleneksel olarak daha erken dönemlere ait, yani XIV. yüzyıldan erken olduğu kabul edilen vakayinameler için ilginç sonuçlar vereceğini göreceğiz.
Yukarıda maksimumların korelasyon ilkesini istatistiksel detayları geçerek kabaca betimledik, çünkü amacımız okuyucularımız tarafından hızlı şekilde anlaşılmaktır. Aynı zamanda yöntemin titiz matematiksel anlatımı ve arıtılması epeyce ayrıntı verilmesini gerektirir. Betimlenen yöntemi daha derin bir şekilde anlamak isteyen okuyucuyu bilimsel yayınlara [884], [892] yönlendiriyoruz.
p(X,Y) katsayısını X ve Y vakayinamelerinde ayrıntılı olarak anlatılan senelerin rastlantısal kesişme olasılığı, yani SRKO olarak adlandırabiliriz.
Yazarın fikrinin ileri düzeydeki gelişimi ve uyarlanması V.V. Fedorov, ve A.T. Fomenko [868], V.V. Kalaşnikov, S.T. Raçev ve A.T. Fomenko’nun [357] yapıtlarında gösterilmiştir. Daha sonra, maksimumların korelasyon ilkesinin, hacmi ve “betimleme yoğunluğu” benzer olan tarihî metinlerin karşılaştırılmasında kendini belirgin bir şekilde gösterdiği ortaya çıktı. Bazı durumlarda, açıkça bağımlı metinlerin yalnız lokal maksimum noktalarının değil, kendi hacim fonksiyonlarının, yani genliklerinin bile birbirlerine yakın olduğu ve uyuştuğu belli oldu! Bu gayet şaşırtıcı ve önemli bir olgudur. Hacim fonksiyonlarının genliklerinin korelasyonu, “gayet fakir” metinlerin, yani kendisinde yansıtılmayan zaman aralıkları büyük olan vakayinamelerin karşılaştırılmasında çok belirgin şekilde gözlenmektedir. Vakanüvisler tarafından “gayet fakir” vakayinamelerin yazılmasının, “bilgiye saygı” ya da “nadirlerin korunması” ilkelerine uyduğu belli oldu. Bu eğilim S.T. Raçev ve A.T. Fomenko [723],[1140] tarafından keşfedilmiştir. Ayrıca bu konudaki hazırlık araştırmaları ve bilgiye karşı saygı ilkesinin formüle edilmesi için hem [723], [1140] eserlerine hem de “Tarihleri Değiştiriyoruz Her Şey Değişiyor” kitabına, bölüm 3:1’e bakınız.
Maksimumların korelasyonu ilkesi M.S. XVI. yüzyılın sonu–XVII. yüzyılın başındaki Karışıklık Dönemi’ne ait bazı Rus vakayinamelerinin analizinde başarıyla uygulanmıştır. Bu konuda L.E. Morozova ve A.T. Fomenko’nun [902],[548] eserlerine bakınız. N.S. Kellin’in de bu araştırmalara büyük katkısı var. Elde edilen sonuçlar “Tarihleri Değiştiriyoruz Her Şey Değişiyor” kitabının 3:2 bölümünde anlatılmıştır.
