Parte 2: LA CINA. LA NUOVA CRONOLOGIA E LA CONCEZIONE DELLA STORIA CINESE. LE NOSTRE IPOTESI.
Capitolo 5: Le comete cinesi.
5. La cometa di Halley.
5.1. Introduzione.
La cometa di Halley è la cometa più famosa di tutte.
La cometa di Halley è anche la cometa più spettacolare di tutte.
La cometa di Halley è uno dei fondamenti principali della cronologia cinese e della teoria moderna sulla grande antichità della civiltà cinese.
Si ritiene che i cinesi abbiano osservato tutti gli spostamenti di questa cometa almeno dal I secolo a.C. ad oggi. Si ritiene che la moderna teoria del moto della cometa di Halley sia confermata dalle antiche cronache cinesi; questa teoria, a sua volta, conferma la cronologia scaligeriana della Cina. Nella fig. 5.6 riproduciamo un'antica rappresentazione della cometa dall'antico tappeto di Baille. La storia di Scaligero cerca di convincerci che la cometa in questione sia la cometa di Halley vista nel presunto anno 1066.
Persino Morozov, nella sua revisione radicale di molti strati della storia antica, mette in dubbio solo la veridicità dei documenti cinesi riguardanti la cometa di Halley prima dell'inizio della nuova era, ritenendoli più o meno corretti in seguito.
Egli fa la seguente confusa affermazione: “Qualunque sia l’origine di queste registrazioni di comete cinesi, alcune di esse sono in sorprendente concomitanza con le ricorrenze teoricamente calcolate della cometa di Halley, il che ci porta a trattarle seriamente come un valido mezzo per la verifica degli antichi documenti”. che contengono descrizioni di comete" ([544], Volume 6, pagina 156).
Per cui, non vi sono ragioni apparenti per diffidare della cronologia cinese, basata tra l’altro sulle ricorrenze della cometa di Halley; persino Morozov ne era convinto, sebbene nutrisse una serie di seri sospetti: “La cometa di Halley non conferma le segnalazioni di She-Ke e del “Cavallo della Foresta” riguardanti i primi secoli d.C. Che diritto abbiamo di supporre che questi libri possano dimostrare una scala cronologica che si estende più indietro nel passato?” ([544], Volume 6, pagina 154).

Figura 5.6. Cometa raffigurata su un tappeto antico di Baille. Gli storici la identificano come la cometa di Halley e datano l'osservazione al presunto anno 1066. Il tappeto fu presumibilmente realizzato intorno al 1073-1083. È conservato nella biblioteca comunale di Baille e realizzato in lana su lino. L'immagine è riprodotta in [930] come un frammento del "tappeto medievale più lungo e famoso che può servire anche come cronaca storica" ([930], pagina 161). Tratto da 930, pagina 161. Vedere anche la copia disegnata in [544], Volume 6, pagina 144.
Tuttavia, la situazione qui non è così semplice come potrebbe sembrare in origine. L'analisi di Morozov si è rivelata qui incompleta. Non avrebbe dovuto considerare “sorprendente” la corrispondenza tra alcuni degli “antichi” documenti cinesi e il ciclo di ricorrenza calcolato della cometa di Halley: la nostra analisi dimostra che la probabilità che detta corrispondenza sia una mera coincidenza è abbastanza alta; molte di queste corrispondenze risultano infatti puramente casuali, vedere sotto. Tuttavia, per fortuna, i creatori della "antica” cronologia cinese hanno rifiutato di fermarsi qui, tentando di portare l’intero quadro alla “perfezione”. Hanno commesso un errore, avendo aggiunto diverse registrazioni cinesi “antiche” dei presunti avvistamenti della cometa di Halley nel XVIII secolo e lasciando così una prova schiacciante che permette di dimostrare la falsità dell’intera cronologia cinese “antica”. Il falso in questione è stato commesso nel XVIII secolo.
5.2. L’analisi dei cicli di ricorrenza del Pianeta Halley.
5.2.1. L’elenco delle date dei presunti avvistamenti della Cometa di Halley.
Cominciamo con l'elenco delle date tradizionalmente associate agli avvistamenti della cometa di Halley. Di solito è diviso in due parti, vale a dire la registrazione cinese e quella europea delle osservazioni della cometa di Halley. Citiamo entrambi gli elenchi e confrontiamoli tra loro.
Gli astronomi Cowell e Crommelin hanno utilizzato queste date come base per la teoria astronomica e matematica del moto della cometa di Halley all’inizio del XX secolo. Hanno usato questa teoria per i loro calcoli teorici dei cicli ricorrenti delle comete nel passato. Nella tabella seguente riportiamo i risultati dei loro calcoli teorici nonché gli anni delle presunte osservazioni europee e cinesi legate alla cometa di Halley. I nomi dei mesi nella colonna di sinistra indicano il passaggio della cometa attraverso il punto del perielio.
Mesi |
Teoria di Cowell e Crommelin. Calendario giuliano. |
Date tradizionali delle registrazioni cinesi (secondo lo She-Ke). |
Date tradizionali indicate nelle cronache europee. |
Aprile |
1910 |
1910 |
1910 |
Marzo |
1835 |
1835 |
1835 |
Marzo |
1759 |
1759 |
1759 |
Settembre |
1682 |
1682 |
1682 |
Ottobre |
1607 |
1607 |
1607 |
Agosto |
1531 |
1531 |
1531 |
Giugno |
1456 |
1456 |
1456 |
Novembre |
1378 |
1378 |
-- |
Ottobre |
1301 |
1301 |
1301 |
Settembre |
1222 |
1222 |
1222 |
Aprile |
1145 |
1145 |
1145 |
Marzo |
1066 |
1066 |
1066 |
Settembre |
989 |
989 |
-- |
Luglio |
912 |
912 |
912 |
Febbraio |
837 |
837 |
837 |
Luglio |
760 |
760 |
- (761?) |
Novembre |
684 |
684 |
684 |
Marzo |
607 |
607 |
-(607?) |
Novembre |
530 |
532 |
531 |
Luglio |
451 |
451 |
-(450?) |
Novembre |
373 |
373 |
-- |
Aprile |
295 |
296? |
-- |
Aprile |
218 |
218 |
217 |
Marzo |
-141 |
141 |
-- |
Gennaio |
66 |
66 |
66 |
Ottobre |
-12 |
-11 |
-12 |
Agosto |
-86 |
-86 |
-86 |
Non si trovano altre menzioni della cometa di Halley né nelle fonti cinesi né in quelle europee, a parte qualche rara eccezione. Ad esempio, la documentazione cinese del 239 a.C. è talvolta considerata un riferimento alla cometa di Halley ([544], Volume 6, pagina 140). Vedere il grafico di Cowell e Crommelin e l'elenco delle comete a pagina 73 della fonte sopra menzionata.
La prima impressione che si ha è che la tabella ci porta inequivocabilmente alla seguente conclusione fondamentale: la teoria matematica del moto della cometa di Halley è in ottima corrispondenza con le osservazioni dei cinesi. A proposito, la corrispondenza di detta teoria con le fonti europee è assai peggiore. Evitiamo però di essere eccessivamente critici: dopo tutto, è risaputo che gli astronomi cinesi erano noti per la loro meticolosità, soprattutto nel lontano passato, ben distanti dai loro colleghi europei.
Ribadiamo: il grafico teorico appare conformato dalla coincidenza di tutte le date teoriche con quelle desunte dalle cronache cinesi, ad eccezione di una discrepanza di due anni e di due discrepanze di un anno. In realtà, le discrepanze annuali possono essere trascurate, a causa di una certa ambiguità riguardante l'inizio dell'anno nell'antichità.
5.2.2. Cosa è successo alla cometa di Halley nel 1986? Le ragioni per cui si è spostata nell'altro emisfero.
Bisogna sottolineare in particolare il fatto che si ritiene che gli astronomi cinesi abbiano osservato ogni singola apparizione della cometa di Halley nel corso di duemila anni senza perderne nessuna.
La Cina si trova nell’emisfero settentrionale. A parte questo, ogni descrizione del percorso di una cometa identificata oggi come cometa di Halley, si riferisce alle costellazioni dell'emisfero settentrionale o dello zodiaco. Abbiamo confrontato questo con l'elenco delle comete in [544], Volume 6.
L’inevitabile conclusione è che ogni singola apparizione della cometa di Halley negli ultimi duemila anni era teoricamente osservabile esclusivamente dall’emisfero settentrionale.
Finora tutto sembra comprensibile e naturale. Una grande cometa ricorrente segue la stessa orbita stazionaria, più o meno stabile rispetto all'eclittica, da duemila anni.
Chiediamo ai lettori residenti nell'emisfero settentrionale se hanno visto la cometa di Halley nel 1986? La risposta è negativa. Il motivo è semplicissimo: non era visibile dall’emisfero settentrionale e poteva essere osservata solo da quello meridionale (ed era piuttosto debole).
Cosa potrebbe essere successo alla cometa di Halley? Duemila anni di osservazioni dall'emisfero settentrionale seguite da un'improvvisa migrazione verso quello meridionale? I nostri avversari potrebbero suggerire che questo fatto sia una conseguenza della legge matematica del suo movimento. Proprio questa legge matematica è ciò che considereremo nella sezione seguente.
Per il momento facciamo un riassunto. Un cambiamento così drastico nel modello di movimento di una cometa rimasta stabile per duemila anni, ci sembra davvero molto strano.
Quanto sopra ci fa dubitare fortemente della veridicità della cronologia tradizionale degli avvistamenti della cometa di Halley. Tutte le sue apparizioni si riflettono fedelmente nelle cronache cinesi? Potremmo trovarci di fronte a coincidenze casuali o, peggio ancora, a inserimenti successivi nel testo? A proposito, qual è la probabilità che una “curva sinusoidale periodica” arbitraria coincida casualmente con le date tradizionali accettate, che si trovano nei documenti cinesi? Forniremo la risposta a questa domanda di seguito; saltando in avanti, possiamo dire ai lettori che tale probabilità è in realtà piuttosto alta.
5.2.3. Cosa è successo alla cometa di Halley dopo il 1759? Il motivo per cui i suoi cicli di ricorrenza sono diventati irregolari.
La sequenza di date suggerite per indicare le apparizioni della cometa di Halley negli elenchi cinesi ha una caratteristica molto strana. Rivela una regolarità centenaria eccezionalmente precisa nei cambiamenti dei cicli di ricorrenza della cometa di Halley, che si ritiene sia caratterizzata da un’eccezionale stabilità. Ci riferiamo alla legge scoperta dagli astronomi Cowell e Crommelin, che studiarono i registri delle comete cinesi ([544], Volume 6).
Riproduciamo il grafico che hanno costruito nella fig. 5.7.
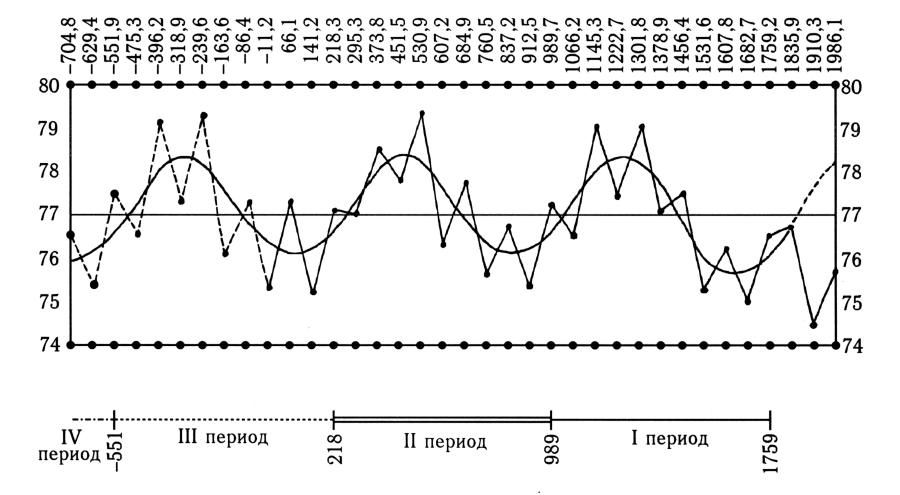
Figura 5.7. Il grafico mostra le fluttuazioni degli intervalli di tempo tra le osservazioni della cometa di Halley secondo la cronologia di Scaligero. La linea orizzontale corrisponde alle date di Scaligero delle osservazioni della cometa di Halley, e quella verticale alle distanze tra le osservazioni delle comete espresse in anni. Il grafico è ovviamente di natura periodica; i confini dei periodi risultanti sono indicati in basso.
Sull'asse orizzontale abbiamo gli anni in cui venne osservata la cometa di Halley secondo la cronologia cinese. Le date sono riportate con il margine di precisione di un decimo di anno.
Sull'asse verticale vediamo i periodi di ricorrenza della cometa di Halley, ovvero gli intervalli tra le sue riapparizioni consecutive. Ad esempio, l'intervallo tra la sua ultima apparizione del 1986.1 e la precedente del 1910.3 è pari a 75,8 anni ecc. Questi numeri sono indicati sotto il grafico.
Il grafico rivela una distinta regolarità periodica manifestata con accelerazioni e decelerazioni centenarie nel movimento della cometa di Halley, con un periodo di 77,0 anni. La curva sinusoidale livellata corrisponde ai valori modificati degli intervalli di ricorrenza.
La curva a dente di sega corrisponde ai periodi consecutivi di ricorrenza della cometa calcolati dalle cronache cinesi. A questo riguardo chiameremo questa curva “sperimentale”. Bisogna sottolineare che le date teoriche calcolate dagli astronomi per i cicli di ricorrenza della cometa di Halley sono in ottima corrispondenza con gli “esperimenti cinesi”. Questo fatto confuse moltissimo Morozov e lo convinse in parte che le date cinesi degli avvistamenti della cometa di Halley negli ultimi millecinquecento anni della nuova era, fossero veritiere.
Analizziamo ora la curva “sperimentale cinese” a dente di sega. Si scopre anche che l’intervallo di dispersione dei punti “sperimentali” attorno alla curva sinusoidale, è tutt’altro che casuale. Questo grafico a dente di sega, presumibilmente sperimentale, è anche di fatto strettamente periodico. Tre dei suoi periodi sono indicati nella fig. 5.7:
1) Tra i presunti anni 551 a.C. e 218 d.C. (estrapolazione apparente, poiché si presume che i cinesi non avessero informazioni sulla cometa di Halley per una parte di quest'epoca),
2) Tra i presunti anni 218 d.C. e 989 d.C.,
3) Tra i presunti anni 989 d.C. e 1759 d.C.
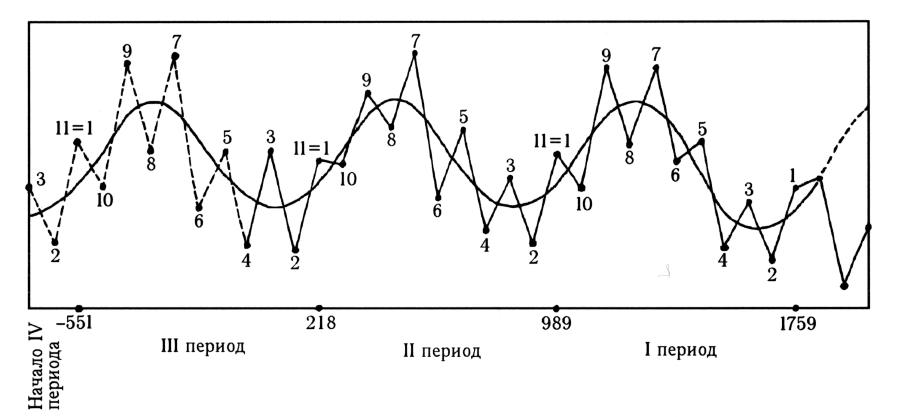
Figura 5.8. Grafico precedente degli intervalli di tempo fluttuanti tra le osservazioni della cometa di Halley. Qui abbiamo assegnato lo stesso numero ad ogni punto corrispondente entro un dato periodo.
Nella fig. 5.8 abbiamo assegnato un numero da 1 a 10 ai punti “sperimentali” compresi in ciascun periodo. È perfettamente ovvio che il segmento della curva a dente di sega numerato 1, 2, . . ., 10 si ripete tre volte, quasi senza variazioni.
Questo effetto è particolarmente dimostrabile nella fig. 5.9, dove i detti tre segmenti della curva a dente di sega sono sovrapposti tra loro. Nonostante le piccole discrepanze tra le tre curve, possiamo vedere chiaramente che sono praticamente identiche.
Pertanto, la curva “sperimentale” dei periodi di ricorrenza della cometa di Halley è strettamente periodica, essendo il periodo pari all’incirca a 770 anni. Sarebbe quindi normale aspettarsi che questa legge, che teoricamente è valida per due millenni, conservi la sua validità fino ai giorni nostri.
Per i matematici bisogna aggiungere che questa curva è ben approssimata dalla relazione funzionale reale-analitica, come soluzione di un problema analitico di matematica celeste. Pertanto, il fatto che dimostri un comportamento strettamente periodico entro un certo intervallo, implica che dovrebbe comportarsi con una periodicità simile su tutta la linea dei numeri reali. In altre parole, dovrebbe rimanere periodica anche nel prossimo futuro.
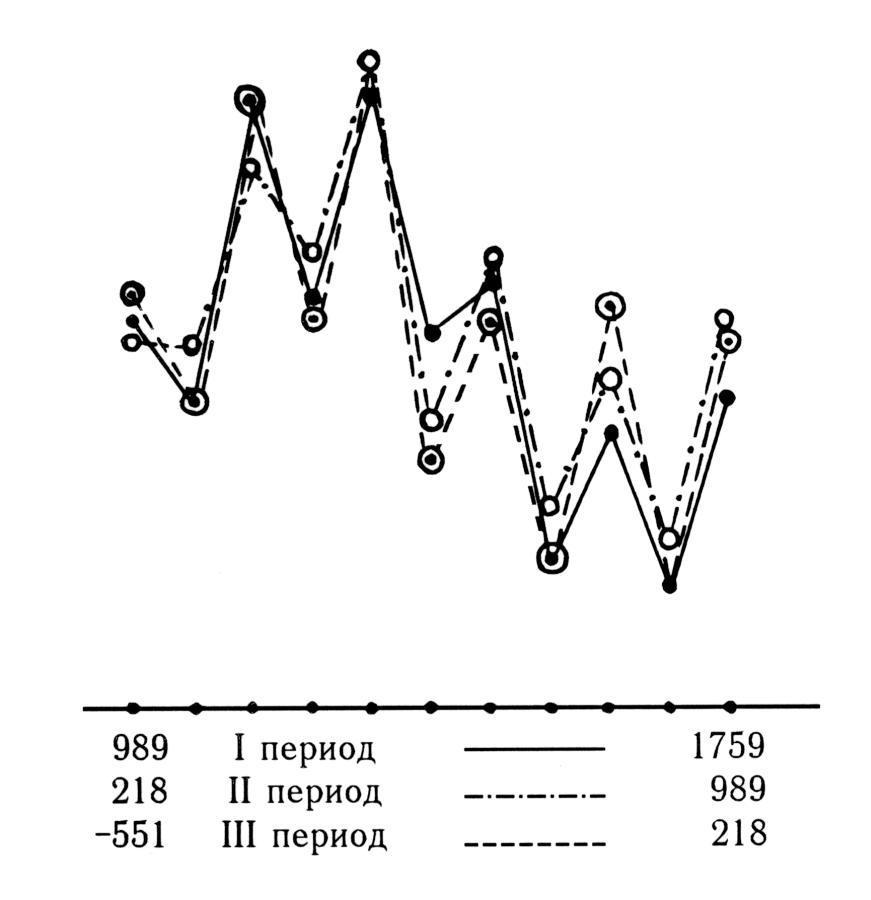
Figura 5.9. Sovrapposizione dei tre periodi immaginari nel comportamento della cometa di Halley. Ciò vuol dire che la cometa di Halley si è comportata esattamente nello stesso modo per ben tre volte.
Cosa vediamo nella realtà? Ritorniamo alla fig. 5.7. Se la cometa di Halley avesse continuato a muoversi secondo la sua legge di fluttuazione dell’intervallo di ricorrenza centenaria, presumibilmente periodica, la curva reale di questi intervalli si sarebbe spostata nella direzione della linea tratteggiata di Cowell e Crommelin dopo il 1759, o avrebbe manifestato intervalli di ricorrenza crescenti. Tuttavia, scopriamo che nella realtà è vero il contrario.
Ciò è particolarmente evidente nella fig. 5.10. La spessa curva nera corrisponde al comportamento degli intervalli di ricorrenza della cometa di Halley negli anni 1759, 1835, 1910 e 1986. Questa curva smentisce completamente la “legge sperimentale cinese”, che si dice sia rimasta valida per due millenni.
A quanto pare, Morozov fu il primo a dubitare della validità di questa “legge periodica”. Il suo commento è il seguente:
“La cometa è apparsa nel 1910, anticipando la data prevista di 3,5 anni. Questo fatto ci dà motivo di sospettare una certa arbitrarietà anche nella selezione delle date medievali, possibilmente volta a convalidare la curva sinusoidale delle accelerazioni e delle decelerazioni" ([544], Volume 6, pagina 138).
Diversi decenni dopo, quando la cometa di Halley riapparve prima di quanto previsto dalla “legge cinese”, possiamo affermare con ancora maggiore sicurezza che la cronologia consensuale della ricorrenza della cometa di Halley contiene gravi errori.
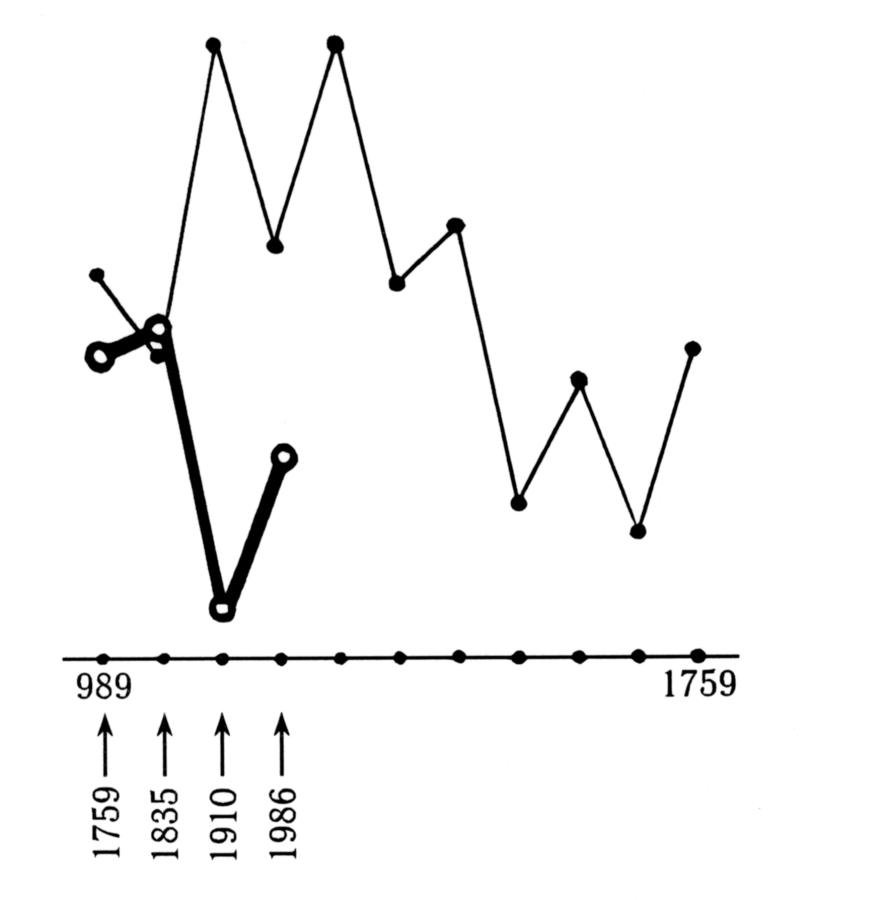
Figura 5.10. Le interruzioni nella falsa periodicità del comportamento della cometa di Halley scoperta nel XX secolo. Questo fatto infligge un colpo mortale alla cronologia scaligeriana delle osservazioni della cometa di Halley che segue le “antiche” cronache cinesi.
La Fig. 5.11 mostra il comportamento degli intervalli di ricorrenza della cometa di Halley nel corso degli ultimi seicento anni, cioè tra il 1301 e il 1986 d.C. Poiché possiamo più o meno fidarci della cronologia di Scaligero di questo intervallo di tempo, ha senso supporre che la Fig. 5.11 corrisponde al comportamento reale della cometa di Halley, a condizione che le sue apparizioni nel XIV-XV secolo d.C. siano state identificate correttamente nei registri cinesi ed europei. Tuttavia, abbiamo già detto che abbiamo tutte le ragioni per dubitare della correttezza di tali identificazioni, altrimenti, perché la traiettoria della cometa osservata nel 1378, identificata condizionatamente come cometa di Halley, confonderebbe così tanto l’astronomo Pingré (vedi sopra)?
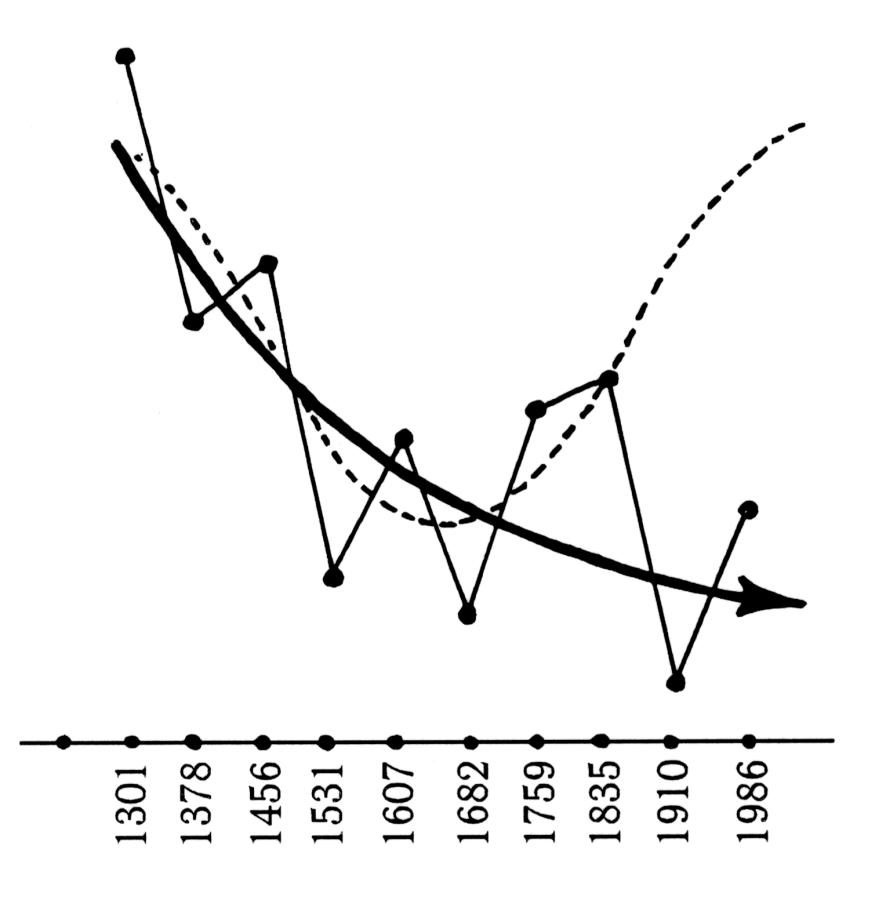
Figura 5.11. Il comportamento reale della cometa di Halley negli ultimi seicento anni è disegnato con la curva spessa. La linea tratteggiata dimostra come la cometa di Halley avrebbe dovuto comportarsi secondo la falsa legge periodica degli “antichi” documenti cinesi. Analogamente ai grafici precedenti, le date delle osservazioni della cometa di Halley sono sulla linea orizzontale, e gli intervalli tra le osservazioni sono sulla linea verticale.
Tuttavia, per il momento concordiamo con la cronologia di Scaligero e assumiamo che ogni apparizione della cometa di Halley nel corso degli ultimi sei secoli sia stata identificata correttamente nelle rispettive osservazioni cinesi ed europee.
Cosa vediamo? La curva approssimata degli intervalli di tempo, rappresentata come una spessa linea nera nella fig. 5.11, ovviamente recede, il che implica la riduzione media degli intervalli di ricorrenza della cometa di Halley. È del tutto evidente che la linea tratteggiata che rappresenta l'ipotetica “legge cinese” di Cowell e Crommelin non corrisponde alle reali apparizioni della cometa di Halley nel corso degli ultimi seicento anni.
In altre parole, la cometa viene avvistata sempre più spesso nelle vicinanze del Sole. Le ragioni di questa tendenza rimangono poco chiare: l’orbita della cometa di Halley potrebbe essere influenzata da fluttuazioni sostanziali e potrebbe accelerare. È possibile che cominci a disintegrarsi nel suo complesso. Solo i suoi futuri avvistamenti potranno far luce sulla questione: al momento non disponiamo di dati sufficienti per prevederne l’evoluzione.
Tuttavia si può affermare in modo più o meno definitivo che ogni ricomparsa della cometa rivela cambiamenti sostanziali nel suo comportamento, il che significa che non vi è alcuna ragione per supporre che le sue passate apparizioni fossero caratterizzate da una qualsiasi periodicità.
Questo ci porta ad una conclusione molto importante. Tenendo conto di tutte le considerazioni sopra esposte, dobbiamo ammettere che la “curva cinese a dente di sega”, come presunta funzione del ciclo di ricorrenza della cometa di Halley, è manifestamente falsa. Non è possibile che rifletta i reali avvistamenti o la reale traiettoria della cometa. Si tratta quindi o di natura casuale, oppure di una falsificazione, tutto sommato, premeditata o involontaria e frutto delle “migliori intenzioni”. Discuteremo questo problema più avanti.
5.2.4. La provenienza della “legge cinese della periodicità” per la cometa di Halley.
Ci si può porre la seguente domanda, del tutto giustificata: se il comportamento della cometa di Halley è effettivamente privo di periodicità, da dove ha avuto origine la curva sperimentale a dente di sega che ha fornito a Cowell e Crommelin un fondamento per la loro ipotesi? Dopotutto, sono riusciti a individuare ogni singolo punto del grafico nei vecchi elenchi di comete e a sistemarli perfettamente secondo la “legge cinese della periodicità”. È possibile che tutte le osservazioni cinesi siano state contraffatte per dimostrare la periodicità dei cicli di ricorrenza della cometa di Halley nel corso degli ultimi duemila anni? Non si può negare il fatto che il grafico della fig. 5.7 contiene almeno 17 punti che rappresentano l'epoca precedente al XIV secolo. È possibile che ognuno di essi sia frutto di un falso?
Questo non è il caso, ovviamente. Tuttavia, la nostra analisi dimostra che in realtà è avvenuta una falsificazione parziale; contemporaneamente, come dimostreremo tra breve, non era necessario fabbricare diverse decine di registrazioni. La struttura dell’elenco delle comete cinesi, per quanto densa, è tale che la fondatezza di quasi ogni “legge di periodicità” richiederebbe la fabbricazione (inserimento) di un massimo di tre osservazioni.
Soffermiamoci su questo per un po'.
Il fatto è che l’elenco delle comete cinesi è eccezionalmente denso; in altre parole, contiene una grande varietà di “avvistamenti di comete” registrati. Supponiamo che qualcuno si ponga l'obiettivo di integrare in esso una certa “legge della periodicità”, che si riduce al compito di scoprire una serie periodica di osservazioni separate da intervalli uguali di 76 anni, 80 anni, 120 anni ecc. E' fattibile?
A dir il vero, si. Inoltre, è possibile implementarla per quasi ogni dato valore di periodicità: possiamo trovare una “cometa” con un ciclo di ricorrenza di 55 anni, 101 anni e così via. Tuttavia, in alcuni casi la periodicità ideale richiederà l'inserimento di due o tre osservazioni nell'elenco delle comete. I valori di intervallo che complicherebbero la formulazione di tale “legge della periodicità”, a causa della necessità di aggiungere troppe “osservazioni” all’elenco, sono pochi e rari.
Cominciamo la nostra dimostrazione con l'osservazione della cometa di Halley che risale al 1607, che si trova all'estremità dell'elenco cinese. Riteniamo che questo documento sia veritiero: dopo tutto risale a un'epoca recente come il XVII secolo.
Abbiamo cercato di trovare un'osservazione adatta per ogni data precedente coperta da un passo con un valore fisso. Risulta che la maggior parte di tali valori di intervallo definiti a priori, corrisponderanno alle osservazioni effettive contenute negli elenchi delle comete cinesi con il margine di precisione massimo di tre anni, con non più di tre lacune per l'intero elenco, vedi nella tabella seguente.
Pertanto, l’inserimento di una o due osservazioni nell’elenco delle comete cinesi è sufficiente per utilizzare quest’ultimo per la convalida di qualsiasi legge di periodicità centenaria per la cometa di Halley. Inoltre, qualsiasi ciclo di ricorrenza può essere dimostrato in questo modo abbastanza facilmente. Le eccezioni sono estremamente rare: ci sono pochissimi valori effettivi di periodicità “sfortunati”, che non corrispondono completamente ai dati sperimentali cinesi.
La cometa di Halley non ha nulla a che fare con queste questioni, l'unica ragione è l'altissima densità cronologica dell'elenco delle comete cinesi, che rende possibile scoprire qualsiasi tipo di periodicità nel movimento di qualsiasi cometa.
Riportiamo la tabella di corrispondenza tra i diversi “valori di periodicità” delle apparizioni della cometa di Halley e i dati “sperimentali” cinesi per il periodo compreso tra il 100 a.C. e il 1607 d.C.
La prima colonna della tabella contiene il valore del “periodo”; abbiamo provato ogni valore compreso tra 50 e 200 anni, calcolando tutte le possibili discrepanze (in anni) tra le date “teoriche” dei ripetuti avvistamenti della cometa di Halley nel passato, come determinato per questo “periodo”, e le date “sperimentali” più adatte dall’elenco delle comete cinesi per ciascuno di detti valori. I valori di discrepanza risultanti sono stati quindi disposti in ordine decrescente e contrassegnati con d1, d2, d3 ecc. I primi quattro valori di questa sequenza decrescente (o meglio non crescente) si trovano nelle colonne 2-5 della nostra tabella.
Pertanto, la seconda colonna contiene il valore massimo della discrepanza (in anni) tra gli avvistamenti “teorici” della cometa di Halley nel passato, calcolati per un dato “periodo” e le migliori corrispondenze dell'elenco delle comete cinesi. La terza colonna contiene il secondo valore di discrepanza più grande. La quarta e la quinta sono attribuite ai due valori successivi in ordine decrescente. Pertanto, indichiamo i quattro maggiori valori di discrepanza per un dato “periodo”, che rappresentano la differenza tra i dati cinesi e la legge di periodicità dei cicli di ricorrenza della cometa di Halley formulata per il “periodo” in questione.
Tabella. Confronto tra i dati cinesi della cometa e le riapparizioni “teoriche” della cometa di Halley, calcolate per valori di periodicità di ricorrenza scelti casualmente. Il confronto copre l'intervallo tra il 100 a.C. e la fine dell'elenco delle comete cinesi. |
||||
| Valore del periodo |
d1 |
d2 |
d3 |
d4 |
| 50 | 15 | 7 | 3 | 1 |
| 51 | 23 | 10 | 4 | 1 |
| 52 | 31 | 8 | 1 | 1 |
| 53 | 32 | 4 | 4 | 1 |
| 54 | 24 | 6 | 1 | 1 |
| 55 | 16 | 5 | 2 | 2 |
| 56 | 14 | 10 | 3 | 0 |
| 57 | 16 | 14 | 7 | 4 |
| 58 | 21 | 5 | 4 | 0 |
| 59 | 28 | 11 | 3 | 0 |
| 60 | 35 | 7 | 3 | 3 |
| 61 | 29 | 6 | 5 | 1 |
| 62 | 22 | 9 | 7 | 0 |
| 63 | 22 | 15 | 15 | 11 |
| 64 | 13 | 8 | 8 | 8 |
| 65 | 10 | 7 | 5 | 5 |
| 66 | 16 | 11 | 3 | 3 |
| 67 | 17 | 17 | 5 | 1 |
| 68 | 23 | 4 | 1 | 0 |
| 69 | 29 | 7 | 1 | 1 |
| 70 | 35 | 10 | 6 | 1 |
| 71 | 30 | 12 | 8 | 3 |
| 72 | 24 | 7 | 4 | 1 |
| 73 | 18 | 2 | 0 | 0 |
| 74 | 20 | 12 | 2 | 1 |
| 75 | 19 | 9 | 6 | 3 |
| 76 | 16 | 11 | 5 | 5 |
| 77 | 3 | 3 | 2 | 2 |
| 78 | 14 | 10 | 6 | 6 |
| 79 | 10 | 2 | 2 | 1 |
| 80 | 15 | 6 | 2 | 2 |
| 81 | 22 | 20 | 6 | 3 |
| 82 | 25 | 2 | 2 | 0 |
| 83 | 30 | 2 | 2 | 2 |
| 84 | 35 | 6 | 1 | 0 |
| 85 | 31 | 3 | 2 | 1 |
| 86 | 26 | 2 | 2 | 0 |
| 87 | 25 | 21 | 5 | 5 |
| 88 | 16 | 9 | 3 | 1 |
| 89 | 11 | 11 | 2 | 0 |
| 90 | 18 | 7 | 3 | 3 |
| 91 | 15 | 5 | 5 | 5 |
| 92 | 10 | 7 | 7 | 5 |
| 93 | 10 | 9 | 9 | 6 |
| 94 | 22 | 11 | 7 | 0 |
| 95 | 16 | 10 | 6 | 0 |
| 96 | 9 | 8 | 5 | 0 |
| 97 | 7 | 6 | 4 | 0 |
| 98 | 8 | 7 | 7 | 7 |
| 99 | 14 | 11 | 3 | 2 |
| 100 | 15 | 3 | 1 | 0 |
| 101 | 19 | 2 | 0 | 0 |
| 102 | 23 | 4 | 1 | 0 |
| 103 | 27 | 6 | 2 | 0 |
| 104 | 31 | 8 | 1 | 0 |
| 105 | 35 | 6 | 0 | 0 |
| 106 | 32 | 4 | 4 | 1 |
| 107 | 28 | 7 | 2 | 0 |
| 108 | 24 | 6 | 0 | 0 |
| 109 | 20 | 3 | 1 | 1 |
| 110 | 16 | 2 | 0 | 0 |
| 111 | 12 | 3 | 1 | 0 |
| 112 | 14 | 8 | 6 | 2 |
| 113 | 24 | 6 | 4 | 4 |
| 114 | 16 | 11 | 6 | 5 |
| 115 | 13 | 5 | 3 | 2 |
| 116 | 20 | 8 | 5 | 1 |
| 117 | 15 | 8 | 0 | 0 |
| 118 | 11 | 2 | 1 | 0 |
| 119 | 10 | 2 | 0 | 0 |
| 120 | 8 | 7 | 3 | 0 |
| 121 | 14 | 4 | 4 | 4 |
| 122 | 8 | 7 | 7 | 5 |
| 123 | 7 | 6 | 0 | 0 |
| 124 | 10 | 7 | 0 | 0 |
| 125 | 19 | 8 | 0 | 0 |
| 126 | 22 | 9 | 0 | 0 |
| 127 | 13 | 8 | 0 | 0 |
| 128 | 8 | 7 | 0 | 0 |
| 129 | 12 | 6 | 6 | 0 |
| 130 | 10 | 7 | 5 | 5 |
| 131 | 10 | 8 | 5 | 4 |
| 132 | 11 | 3 | 3 | 0 |
| 133 | 14 | 2 | 0 | 0 |
| 134 | 17 | 1 | 1 | 0 |
| 135 | 20 | 0 | 0 | 0 |
| 136 | 23 | 2 | 1 | 0 |
| 137 | 26 | 4 | 2 | 0 |
| 138 | 29 | 6 | 1 | 0 |
| 139 | 32 | 8 | 0 | 0 |
| 140 | 35 | 10 | 1 | 0 |
| 141 | 33 | 10 | 1 | 0 |
| 142 | 30 | 8 | 0 | 0 |
| 143 | 27 | 6 | 1 | 0 |
| 144 | 24 | 4 | 1 | 0 |
| 145 | 21 | 2 | 0 | 0 |
| 146 | 18 | 0 | 0 | 0 |
| 147 | 15 | 1 | 0 | 0 |
| 148 | 12 | 2 | 1 | 0 |
| 149 | 9 | 4 | 0 | 0 |
| 150 | 6 | 3 | 0 | 0 |
| 151 | 10 | 6 | 3 | 1 |
| 152 | 11 | 4 | 1 | 1 |
| 153 | 5 | 3 | 1 | 1 |
| 154 | 3 | 2 | 0 | 0 |
| 155 | 10 | 10 | 3 | 2 |
| 156 | 14 | 6 | 6 | 2 |
| 157 | 7 | 4 | 3 | 0 |
| 158 | 5 | 4 | 2 | 0 |
| 159 | 10 | 4 | 4 | 1 |
| 160 | 14 | 8 | 8 | 6 |
| 161 | 21 | 13 | 8 | 2 |
| 162 | 22 | 18 | 6 | 1 |
| 163 | 19 | 8 | 4 | 0 |
| 164 | 14 | 5 | 5 | 2 |
| 165 | 9 | 9 | 4 | 2 |
| 166 | 5 | 4 | 4 | 2 |
| 167 | 4 | 4 | 1 | 0 |
| 168 | 8 | 6 | 0 | 0 |
| 169 | 5 | 1 | 0 | 0 |
| 170 | 7 | 3 | 3 | 2 |
| 171 | 8 | 5 | 3 | 0 |
| 172 | 8 | 7 | 4 | 2 |
| 173 | 7 | 3 | 1 | 0 |
| 174 | 5 | 5 | 0 | 0 |
| 175 | 7 | 7 | 0 | 0 |
| 176 | 9 | 9 | 0 | 0 |
| 177 | 11 | 0 | 0 | 0 |
| 178 | 11 | 1 | 0 | 0 |
| 179 | 9 | 2 | 0 | 0 |
| 180 | 7 | 3 | 0 | 0 |
| 181 | 11 | 5 | 5 | 4 |
| 182 | 14 | 10 | 5 | 5 |
| 183 | 8 | 8 | 6 | 0 |
| 184 | 10 | 7 | 0 | 0 |
| 185 | 8 | 0 | 0 | 0 |
| 186 | 10 | 9 | 0 | 0 |
| 187 | 16 | 10 | 0 | 0 |
| 188 | 22 | 11 | 0 | 0 |
| 189 | 22 | 11 | 0 | 0 |
| 190 | 16 | 10 | 0 | 0 |
| 191 | 11 | 9 | 0 | 0 |
| 192 | 8 | 0 | 0 | 0 |
| 193 | 7 | 7 | 0 | 0 |
| 194 | 7 | 6 | 0 | 0 |
| 195 | 8 | 5 | 5 | 5 |
| 196 | 8 | 7 | 4 | 0 |
| 197 | 9 | 3 | 0 | 0 |
| 198 | 11 | 2 | 0 | 0 |
| 199 | 13 | 1 | 0 | 0 |
| 200 | 15 | 0 | 0 | 0 |
Consideriamo l'ultima colonna della tabella. Più della metà dei valori in esso contenuti sono zero. Solo il 10% dei valori di discrepanza supera i tre anni.
Pertanto, nel 90% dei casi l’elenco delle comete cinesi “confermerà” un dato valore di periodo arbitrario come il presunto “valore del ciclo di ricorrenza” della cometa di Halley, e con elevata precisione; il valore massimo di discrepanza non dovrà superare i tre anni in nessuno dei casi. Nel cinquanta per cento dei casi la “corrispondenza” sarà ideale. Il maggior numero di lacune nell'elenco cinese, intendendo con questo la mancata corrispondenza con la data “calcolata teoricamente” in un dato istante, non supera il tre.
Cosa intendiamo, infatti, se affermassimo che il quarto valore di discrepanza tra i dati sperimentali cinesi e gli equivalenti “calcolati teoricamente” non supera i tre anni? Ciò significa che nessun altro valore di discrepanza “teoria vs. esperimento” (con la sola possibile eccezione dei primi tre valori trovati nelle colonne 2-4) supera i 3 anni.
Da qui la teorica “ottima corrispondenza tra la teoria ed i dati sperimentali cinesi”. La struttura dell’elenco delle comete cinesi prevede tali “eccellenti corrispondenze”, indipendentemente dal fatto che la teoria in questione sia corretta o meno.
Torniamo alla nostra tabella. Come è abbastanza facile vedere, uno dei “valori del periodo di ricorrenza della cometa di Halley” teoricamente possibili, risalta distintamente: vale a dire quello di 77 anni. È reso unico dal fatto che quasi ogni singolo presunto avvistamento della cometa di Halley corrispondente ad esso è effettivamente rappresentato nell'elenco cinese. Inizialmente, ci sembra una prova indubitabile della veridicità che convalida l'elenco stesso, le date in esso contenute e la “teoria della cometa di Halley” in generale.
Questa però è solo la prima impressione. In effetti, l’ultimo avvento della cometa di Halley nel 1986 non è stato osservato dall’emisfero settentrionale.
Potrebbe essere questo l’unico caso del genere in millesettecento anni? Questo fatto da solo rende altamente sospetta la “corrispondenza ideale” tra la teoria e "l’esperimento cinese”.
Facciamo notare che l'elenco delle comete europee, che ha una densità ancora maggiore rispetto alla sua controparte cinese, non contiene alcuna ricorrenza quintupla della cometa di Halley, vedi sopra. Pertanto, l'elenco europeo non conferma la periodicità della ricorrenza della cometa di Halley. In realtà, una formulazione più precisa suona come segue: la periodicità delle osservazioni ricorrenti della cometa di Halley non conferma la veridicità dell’elenco delle comete europee.
Come abbiamo dimostrato, anche le discrepanze tra "l’esperimento cinese” e la teoria (con un periodo pari a 77 anni) sono tutt’altro che casuali e possono essere espresse come una curva a dente di sega, vedi sopra. L'insieme di queste circostanze ci porta alla conclusione che quello che abbiamo davanti è chiaramente un caso di falsificazione.
5.2.5. La datazione dell'introduzione dei dati fabbricati nelle “registrazioni di osservazione” della cometa di Halley.
La datazione in questione è abbastanza facile da stimare. Basta dare un'occhiata alla curva di fig. 5.7 e segnare il punto in cui la rigorosa periodicità nel comportamento della curva a dente di sega, costruita per la cometa di Halley, cessa di manifestarsi. Ciò avviene nell'intervallo tra il 1759 e il 1835. In altre parole, a sinistra del segno del 1759, la curva a dente di sega genera due o anche tre copie di se stessa, che sono quasi completamente identiche tra loro. Ciò che vediamo è la presunta “legge della periodicità centenaria” ideale.
Nel 1835 questa “legge” viene infranta per la prima volta, vedi fig. 5.7. Anche se questa primissima discrepanza è lungi dall’essere catastrofica, è comunque chiaramente evidente per la prima volta in duemila anni. Tuttavia, poiché la prima discrepanza era piuttosto lieve, è abbastanza facile capire che Cowell e Crommelin non la consideravano una deviazione dalla loro “legge cinese sulla periodicità” della ricorrenza della cometa di Halley.
Tuttavia, i successivi due avventi della cometa di Halley (nel 1910 e nel 1986) furono del tutto scandalosi dal punto di vista di questa teoria. Bisogna pensare che se Cowell e Crommelin fossero nostri contemporanei, non solo si asterrebbero dal pubblicizzare la loro scoperta della “legge cinese”, ma metterebbero anche in discussione la cronologia dei registri delle comete cinesi, proprio come abbiamo fatto noi.
Inutile dire che le osservazioni mancanti (tre al massimo) non sono state introdotte nell'elenco cinese da Cowell e Crommelin, desiderosi di costruire una curva sinusoidale ideale. Si limitarono a elaborare gli elenchi cinesi disponibili al loro tempo e resi rigidi dalla tradizione.
Uno studio visivo della “curva cinese” ci porta a supporre che l’inserimento delle registrazioni di osservazione fabbricate (al massimo tre), debba essere avvenuto tra il 1759 e il 1835. Questa è l’unica condizione alla quale la legge in questione avrebbe potuto essere formulata con “precisione immacolata”, prima dell'imbarazzante constatazione del 1835, che non fu presa in considerazione dagli autori del falso. Pertanto il falso deve essere anteriore al 1835; tuttavia, è molto probabile che sia anche successivo al 1759.
Ma come può essere vero? Gli elenchi delle comete cinesi non furono pubblicati da Mailla e Gaubil nel XVII secolo (vedi sopra)?
La risposta è la seguente. La versione iniziale dei registri cinesi, infatti, deve essere stata pubblicata nel XVII secolo. Tuttavia, all'inizio del XIX secolo furono pubblicate versioni più dettagliate dei registri cinesi: una di queste fu pubblicata da Biot nel 1846, ad esempio ([544], Volume 6, pagina 42). Questo fatto curioso era già stato sottolineato da N. A. Morozov, il quale non riuscì mai a scoprire nulla sull'origine di questi misteriosi supplementi all'elenco cinese del XVII secolo.
Oggi però ci rendiamo conto che se i supplementi in questione furono introdotti all'inizio del XIX secolo, poco prima della pubblicazione del nuovo elenco cinese esteso, tale circostanza è in buona concomitanza con la nostra ricostruzione. L’elenco cinese iniziale è stato integrato con alcune “osservazioni” progettate per giustificare la “curva sinusoidale cinese” della cometa di Halley.
I responsabili di detta falsificazione non devono essere considerati falsificatori malevoli. Devono essere stati guidati dalle migliori intenzioni possibili. Il fatto è che il ciclo di ricorrenza approssimativo della cometa di Halley doveva essere già noto, possibilmente calcolato nell'epoca di Halley, ovvero nel XVIII secolo, sulla base di tre o quattro osservazioni reali della cometa effettuate nel XVI-XVIII secolo.
Il pensiero scientifico si stava evolvendo e a qualcuno deve essere venuta la brillante idea di cercare le osservazioni ricorrenti della cometa di Halley nell'antichità profonda, come si riflette negli stupendi elenchi cinesi risalenti a tempi immemorabili. Siamo dell’opinione che questa persona non fosse molto al corrente dell’astronomia.
Per qualche ragione, questo misterioso benefattore decise che la durata del periodo di ricorrenza della cometa aveva sempre oscillato attorno al valore medio di 77 anni. Il passo successivo prevedeva la costruzione di un grafico che coprisse gli ultimi sette o ottocento anni, che veniva poi copiato meccanicamente in modo da risalire più indietro nel tempo. Il grafico risultante ha prodotto una curva periodica a dente di sega. L'autore deve essere stato felicissimo di aver trovato quasi tutte le date richieste incluse nel grafico, non riuscendo a capire che qualsiasi altro valore del periodo di ricorrenza avrebbe prodotto gli stessi risultati (109 anni invece di 77, per esempio).
Ripetiamo che l'autore dovette trovarsi a disagio con l'astronomia. Dall'elenco dovevano mancare le due o tre osservazioni volte a “giustificare” la sua “teoria”. Questa dissonanza tra teoria e pratica, che sarebbe percepita come normale da un astronomo professionista, si è trasformata in una minaccia per il modello armonico del paradigma appena creato dall'autore, da qui la decisione di introdurre l'osservazione mancante (in alternativa, l'autore avrebbe potuto trovato qualche documento cinese, interpretando nella chiave desiderata i vaghi dati e le prove in esso contenute). La motivazione doveva essere pura e nobile, come il desiderio di ricostruire il quadro veritiero del lontano passato.
Circa 100-150 anni dopo, Cowell e Crommelin, due astronomi professionisti, fecero la sorprendente scoperta di questo grafico recentemente creato. L’hanno trasformata in una “legge di natura” astronomica, canonizzando di fatto questa costruzione artificiale. Poco dopo, nel 1910, questa legge fu spietatamente infranta dalla natura stessa, quando la cometa di Halley apparve nel cielo 3,5 anni prima di quanto previsto dal “grafico cinese”.
Tutta questa attività deve aver somigliato alla Cabbala medievale, o ai tentativi di molti scienziati di trovare rapporti numerici armoniosi e perfetti nella natura: il grande Keplero che decanta l’armonia universale ne è un buon esempio. Nel passato era particolarmente di moda calcolare le eclissi lunari, gli oroscopi e altre cose simili; a quanto pare, alle comete non è stato risparmiato questo destino.
Concludiamo con un'altra osservazione riguardante il periodo di ricorrenza di 77 anni della cometa di Halley. Se dovessimo considerare l'intero elenco delle comete cinesi e non solo la parte di esso successiva al 100 a.C., come abbiamo fatto sopra, il valore del periodo di 77 anni cesserebbe di essere unico rispetto a tutti gli altri valori possibili. Mancherebbero due punti per la ripetizione ideale, così come molti altri valori del periodo.
5.2.6. Riguardo il carattere caotico del moto della cometa di Halley.
Nel 1989, B. V. Chirikov e V. V. Vyacheslavov pubblicarono un articolo su Astronomia e Astrofisica ([1066]). Dimostrarono che il movimento della cometa di Halley è in gran parte influenzato da un composto casuale. Questo lavoro è stato portato alla nostra attenzione dal professor V. V. Kozlov, membro dell'Accademia russa delle scienze, professore della MSU e dottore in fisica e matematica, nonché da A. I. Neyshtadt, professore della MSU e dottore in fisica e matematica.
Il principale corollario della ricerca degli autori può essere formulato come segue: "È stato dimostrato che il movimento della cometa di Halley è caotico a causa delle perturbazioni causate da Giove" ([1066], pagina 146).
Pertanto, il modello del movimento del pianeta Halley non è affatto determinato, ma piuttosto costruito all’interno del paradigma del caos dinamico; in altre parole, se una certa cometa, come ad esempio la cometa di Halley, ruota attorno ad un’orbita molto allungata che va oltre nell'orbita circolare di Giove, incontra quest'ultimo in una fase casuale ogni volta che ritorna nel Sistema Solare, a causa dell'incompatibilità dei loro periodi di rivoluzione. Giove, essendo un pianeta massiccio, influenza maggiormente la perturbazione della traiettoria della cometa. Pertanto, incontrando il pianeta in una fase casuale, la cometa viene sottoposta a una perturbazione casuale.
A quanto pare, le comete di questo tipo (come descritto dal modello matematico sviluppato in [1066]) sono caratterizzate da dinamiche caotiche. Uno dei parametri più sensibili dell’orbita di una cometa è il tempo del suo passaggio attraverso il perielio, ovvero il tempo impiegato da una determinata cometa per ritornare (il suo periodo). In particolare, il periodo della cometa di Halley è un valore casuale con una dispersione esponenzialmente progressiva.
Tuttavia, la “curva sinusoidale cinese ideale” non avrebbe potuto manifestarsi nel comportamento della cometa di Halley, come risultato di un esperimento casuale.
I nostri oppositori potrebbero fare appello alla possibilità teorica dei miracoli, nonostante la loro scarsità. Non lo neghiamo: ad esempio, una scimmia che preme i tasti di una macchina da scrivere potrebbe produrre un testo coerente e senza errori grammaticali (un romanzo, per esempio). Tuttavia, la probabilità che ciò accada è trascurabilmente piccola, sebbene non sia uguale a zero. Lo stesso vale per la possibilità che la “curva cinese” sia il prodotto di una serie di esperimenti casuali. La probabilità che ciò accada è altrettanto piccola e trascurabile quanto la possibilità che qualche scimmia possa battere a macchina l’intero testo di “Guerra e pace” con gusto e slancio, tutti e quattro i volumi, senza errori o omissioni.
5.2.7. La frequenza sospettosamente alta degli eventi improbabili nella storia di Scaligero.
Sarebbe opportuno fare un'osservazione generale riguardo agli eventi storici di bassa probabilità. Morozov, così come gli autori del presente libro, si imbatterono spesso nel seguente tipo di controargomentazione. Citiamo come esempio uno degli oppositori più qualificati di Morozov: B. A. Rosenfeld, un matematico e autore dell'articolo intitolato "La matematica nelle opere di N. A. Morozov" ([583], pagine 129-138). B. A. Rosenfeld scrisse quanto segue in merito ai numerosi bizzarri paralleli inerenti alla versione tradizionale della storia, come la coincidenza delle durate dei regni caratteristici delle correnti dinastiche di epoche diverse, eventi astronomici ricorrenti e così via:
“Morozov calcolerebbe i tassi di probabilità dei vari eventi; trovandoli infinitesimali, dichiarerebbe tali coincidenze impossibili. Considerazioni di questo genere sono del tutto infondate [? – Aut.], visto che la teoria della probabilità si occupa di eventi di massa e non di eventi individuali. Eventi i cui tassi di probabilità si avvicinano allo zero in qualunque misura, possono ancora realmente verificarsi” ([583], pagina 137).
L’ultima affermazione di B. A. Rosenfeld è in realtà vera. Gli eventi con tassi di probabilità infinitesimi accadono; tuttavia, se si vuole far accadere un certo evento improbabile, è necessario eseguire un gran numero di prove; più precisamente, la sua grandezza deve essere inversamente proporzionale al valore del tasso di probabilità. Pertanto, oltre al tasso di probabilità effettivo di un dato evento, è necessario considerare anche il numero di prove necessarie affinché questo evento si verifichi.
Esiste una disciplina speciale che si occupa proprio di questi argomenti: si chiama matematica statistica. Bisogna dire che le considerazioni di Morozov sono perfettamente valide per quanto riguarda la matematica statistica.
Se volessimo spiegare quanto sopra, a un livello qualitativo, a un lettore profano, dovremmo sottolineare che le obiezioni del tipo “l’evento è improbabile, ma potrebbe comunque essere accaduto per caso”, che sentiamo così frequentemente, non possono essere espresse. spesso: una o due, tre volte al massimo. Sono applicabili anche a singoli eventi e nient'altro; non appena vengono espresse troppo spesso e applicate a intere serie e classi di improbabili coincidenze inerenti alla versione tradizionale della storia, diventano completamente prive di significato.
Alcuni dei nostri lettori potrebbero esprimere lo stesso sentimento riguardo alla cometa di Halley e alla presunta natura casuale della curva cinese, il cui tasso di probabilità è minimo, ma tuttavia maggiore di zero, il che lo rende possibile.
Tuttavia, questo sentimento non sarà altro che l’ennesimo anello di una lunga catena di obiezioni simili. La storia di Scaligero è virtualmente piena di eventi con tassi di probabilità prossimi allo zero. Ogni obiezione di questo tipo ha senso solo come fenomeno individuale: non appena viene sommersa da una moltitudine di obiezioni simili, l'intera moltitudine perde ogni validità e significato.
Sottolineiamo ancora una volta la seguente importante circostanza. Perché tutte queste “coincidenze prodotte in serie” precedono cronologicamente il XVI secolo d.C.? Perché sono inesistenti da quattrocento anni? Qual è il problema con la storia? Come mai si è conformata solo alle regole della teoria della probabilità negli ultimi quattrocento anni, dopo aver ostinatamente ignorato per secoli le leggi della statistica matematica?
5.3. Riguardo la cometa di Carlo V.
La famosa cometa di Carlo V è un esempio spettacolare di come l'elenco delle comete cinesi possa essere utilizzato per dimostrare praticamente qualsiasi cosa. La cometa in questione apparve nel 1556, “era grande, e i cinesi la descrivono in modo simile. 292 anni prima, nel 1264, una cometa simile fu osservata proprio prima della morte di papa Urbano; è registrata anche negli “Annali” (She-Ke). Pingré utilizzò questa fonte per stimare l’orbita della cometa come estremamente simile all’orbita della cometa di Carlo V... Ha identificato entrambe le comete come la stessa cometa, il cui ciclo di ricorrenza è pari a 292 anni. Questa teoria prevedeva la ricerca della stessa cometa nel 972, 680, 388 e 96 d.C. ([544], Volume 6, pagine 157-158).
Inutile dire che gli scienziati sono riusciti a trovare tutte le date necessarie nell'elenco cinese; anche l'elenco europeo le conteneva tutte tranne la prima. Ancora una volta, non c'è nulla di sorprendente in questo fatto: gli elenchi delle comete sono molto densi e le descrizioni che contengono sono abbastanza vaghe da soddisfare qualsiasi gusto in termini di identificazione.
Morozov ha perfettamente scritto di notare che: “Qui tutto sembra essere perfettamente armonioso, proprio come nel caso della cometa di Halley: fonti cinesi ed europee 'confermano' la periodicità della cometa di Carlo V; l'effettiva cometa di Carlo V., a sua volta, conferma la veridicità di questi documenti risalenti all'inizio della nuova era. . . Tuttavia, gli attesi furono presto delusi nella maniera più deplorevole: quando cercarono di prevederne il ritorno intorno al 1858, essa si fece beffe delle loro aspettative non comparendo mai. . . non è stata osservata fino ad oggi, il che è stato davvero un duro colpo per tutte le "convalide" contenute negli annali cinesi" ([544], Volume 6, pagina 159).
Ciò che vediamo è ancora un altro esempio dei tentativi insufficientemente giustificati di utilizzare i fitti elenchi cinesi ed europei per convalidare la periodicità delle comete. Tali tentativi vengono fatti per una sola ragione: gli astronomi si fidano troppo di questi elenchi, non essendo consapevoli del fatto che gli elenchi in questione potrebbero in realtà essere di origine molto recente. Inoltre, la stessa densità di registrazioni contenute nei registri delle comete, che confondono le osservazioni reali delle comete con i loro duplicati moltiplicati in varie cronache, consente di usarli per “convalidare” praticamente qualsiasi cosa.
5.4. Gli strani duplicati con la periodicità di 540 anni, inerenti ai registri cinesi ed europei delle comete.
Morozov scoprì la seguente strana tendenza che caratterizza tutti gli elenchi di comete conosciuti, europei e cinesi, nel corso della sua analisi riferita in [544], volume 6. Tutte le antiche comete che precedono il 59 d.C. ricorrono in un periodo di 540 anni. Inoltre, le grandi lacune, o divari, nelle registrazioni delle osservazioni delle comete, si ripresentano dopo lo stesso periodo di tempo.
Ha scritto quanto segue: “Questo non è affatto un evento casuale; pertanto, sono possibili solo due spiegazioni” ([544], pagina 167).
La prima: le comete “antiche” copiano quelle più recenti.
La seconda: la vita astronomica reale delle comete ha uno strano periodo di 540 anni, che fa sì che tutte le comete “ricorrono” dopo il passaggio di 540 anni.
Morozov aggiunge che è possibile anche una terza spiegazione; crediamo che sia la più vicina alla verità. Uno spostamento di 540 anni "è possibile anche se gli eventi storici associati agli avvistamenti di tutte le comete europee fossero spostati indietro nel tempo di un fattore di 540 o 1080 anni" ([544], Volume 6, pagina 170). Tuttavia, gli spostamenti di 540 e 1080 anni ci sono noti abbastanza bene; sono infatti manifesti nella versione scaligeriana della storia “antica” e possono essere scoperti con una varietà di metodi indipendenti, statistici, astronomici, ecc. In precedenza ne abbiamo discusso molto dettagliatamente.