Глава 1.
НЕКОТОРЫЕ НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ АСТРОНОМИИ И ИСТОРИИ АСТРОНОМИИ
4. СОВРЕМЕННОЕ ЗВЕЗДНОЕ НЕБО.
Для того, чтобы датировать старый звездный каталог на основании содержащихся в нем числовых значений координат звезд, мы должны уметь рассчитывать положения звезд на небесной сфере в различные моменты времени в прошлом. Отправной информацией служит описание современного нам звездного неба. Из этого описания для нас будут иметь значение лишь координаты звезд, скорости их собственных движений, а также звездные величины.
Забегая вперед, отметим, что предлагаемый нами способ датировки работает лишь при условии, что взаимное расположение звезд меняется со временем. Вращение всей небесной сферы вследствие изменения системы координат на ней не может служить для независимой датировки каталога. Подробнее мы будем говорить ниже.
Итак, обсудим те характеристики звезд, которыми мы будем пользоваться.
Величина звезды в современном каталоге -- это число, характеризующее яркость звезды. Чем меньше значение величины, тем звезда ярче. Величины звезд указывались в каталогах еще в древности. Так, Альмагест содержит величины всех перечисленных в нем звезд. Наиболее яркие звезды указаны в нем как звезды первой величины, менее яркие -- второй и т.д. В современных каталогах принята такая же шкала для обозначения яркости. Но величины звезд, вообще говоря, являются в них дробными числами. Например, звезда Арктур, имеющая в Альмагесте величину 1, в современном каталоге "The Bright Star Catalogue" [1197] имеет величину 0,24, а Сириус -- также звезда первой величины в Альмагесте, -- в современном каталоге ярких звезд [1197] имеет величину -1,6. Таким образом, Сириус ярче Арктура, хотя Птолемей считал, что эти звезды одинаково яркие.
Дело, вероятно, в том, что в древности яркость, то есть величина, звезд определялась наблюдателем "на глаз". При этом имели значение цвет звезды, яркость ее окружения и т.д. Поэтому величину звезды оценивали довольно грубо. В настоящее время величина звезд определяется фотометрическим способом. Сравнение величин звезд в Альмагесте с их современными точными значениями, проведенное в труде Петерса и Кнобеля [1339], показывает, что расхождение не превышает, как правило, одной-двух единиц.
При расчете истинных положений звезд в прошлом, мы, в основном, пользовались каталогом ярких звезд [1197], где приведены характеристики приблизительно 9000 звезд до восьмой звездной величины. Напомним, что невооруженным взглядом заметны звезды вплоть до 6-й или 7-й звездной величины. В звездном каталоге Альмагеста, по утверждению Птолемея, содержатся все звезды до 6-й величины в видимой части неба.
Правда, говоря "все", Птолемей явно преувеличил, поскольку в видимой части неба имеется намного больше звезд до 6-й величины, чем в каталоге Альмагеста. Это одна из причин того, что при попытке отождествления звезд Альмагеста со звездами "рассчитанного назад" современного неба иногда возникают неоднозначности. См. главу 2. С другой стороны, естественно считать, что почти все звезды, которые действительно наблюдал Птолемей, или его предшественники, "дожили" до наших дней и описаны в современном каталоге [1197].
Известный астроном XVII века И.Байер предложил новую систему обозначения звезд в созвездии. Вместо словесного описания положения звезды в фигуре данного созвездия он предложил обозначать каждую звезду греческой буквой. Самую яркую звезду созвездия -- буквой α, вторую по яркости -- буквой β и т.д. Например, α Leo -- самая яркая звезда в созвездии Льва. Впоследствии Флемстид (1646--1720 годы) присвоил номера звездам в созвездии, а именно, самая западная звезда получила номер 1, следующая к востоку -- номер 2 и т.д. Номер Флемстида и букву Байера часто ставят рядом при обозначении звезды. Пишут например так: 32 α Leo. Кроме того, звезда может иметь собственное имя. Таких "именных" звезд сравнительно немного. Собственные имена давались лишь звездам, имевшим в старой астрономии особое значение. Например, звезда 32 α Leo имеет собственное имя "Регул" (Regulus).
Из современного каталога [1197] мы использовали следующие характеристики звезд.
1. Прямое восхождение звезды на эпоху 1900 года, которое ниже обозначается через α1900 и выражается в часах, минутах и секундах.
2. Склонение звезды на ту же эпоху, которое обозначается через δ1900 и измеряется в градусах, дуговых минутах и секундах.
3. Величина звезды.
4. Скорость собственного движения звезды. Скорость собственного движения звезды имеет две составляющие. Первая составляющая -- это скорость изменения склонения звезды. Вторая составляющая -- скорость изменения ее прямого восхождения. Однако координатная сетка долгот и широт на сфере неравномерна. При приближении к полюсам меридианы все больше и больше сближаются. Поэтому составляющая скорости звезды в прямом восхождении дает искаженное представление об истинной, так сказать "видимой" скорости звезды на небе в направлении параллели. Из-за этого в некоторых современных звездных каталогах составляющая скорости звезды в прямом восхождении дается в приведенном к экватору виде. Это значит, что она умножается на косинус склонения, после чего ее можно понимать как локально евклидову длину проекции вектора скорости звезды на направление экватора (параллели). Это позволяет сравнивать первые компоненты скоростей звезд независимо от их близости к полюсу. Если скорости даны в неприведенном виде, то такое сравнение требует предварительного пересчета.
В каталогах BS4 [1197] и BS5 (Интернет), которыми мы пользовались, скорости даны в приведенном к экватору виде. В каталогах FK4 [1144] и FK5 (Интернет) скорости к экватору не приведены. Как ни странно, это обстоятельство в описаниях астрономических каталогов иногда вообще не отмечается. Проверку того, в каком виде даны скорости в прямом восхождении, приходится проводить исходя из самих численных значений скоростей.
Скорости собственного движения звезд довольно малы. Как правило, они не превосходят 1" в год, а самые быстрые из видимых невооруженным взглядом звезд, например звезда o2 Eri, μ Cas, движутся со скоростью около 4" в год.
Траектории движения звезд на интересующих нас временн'ых интервалах размером в 2--3 тысячи лет можно считать прямолинейными. То есть каждая из координат звезды на небесной сфере меняется по равномерному закону. Конечно, это приближение верно вне малых окрестностей полюсов.
В качестве стандартной системы координат на небесной сфере в современных звездных каталогах обычно берутся экваториальные координаты на эпоху начала 1900, 1950 или 2000 года. Мы выбрали систему экваториальных координат на эпоху начала 1900 года. Отталкиваясь от этой системы, мы проводили дальнейшие вычисления и пересчеты в системы координат для произвольной эпохи t.
В первую очередь для датировки каталога Альмагеста нам потребуются координаты звезд, имеющих заметное собственное движение. Естественно, мы будем рассматривать только те быстрые звезды, которые, как считается, вошли в Альмагест.
Вопрос о надежности отождествления современных звезд со звездами Альмагеста мы здесь пока не рассматриваем. Мы подробно изучим его ниже. Для решения задачи отождествления важно знать -- имела ли та или иная звезда собственное имя в старых каталогах. Информация о средневековых именах звезд взята нами из каталогов BS4 [1197] и BS5 (Интернет).
Для датировки каталога Альмагеста по собственным движениям нам понадобятся, в частности, следующие два списка звезд из современных каталогов. Эти списки мы здесь только опишем. Сами списки приведены в Приложении 1.
Первый из них мы назовем списком "быстрых" звезд. Составляя его, на первом этапе мы отобрали все звезды, приведенная скорость которых хотя бы по одной из координат не меньше чем 0,1" в год. Затем -- оставили из них лишь звезды, имеющие в своем обозначении греческую букву Байера или номер Флемстида. Это позволило отбросить заведомо бесполезные для датировки Альмагеста звезды. Дело в том, что практически все звезды, отождествленные астрономами со звездами Альмагеста, имеют обозначения Байера или Флемстида, или и те и другие одновременно. Причем, если ту или иную звезду Альмагеста сегодня отождествляют со звездой, не имеющей этих обозначений, это отождествление всякий раз сопровождают серьезные сомнения [1339]. Причина этого понятна. Каталоги Байера и Флемстида появились уже в эпоху ранних телескопических наблюдений, в XVII--XVIII веках. Если некая звезда не вошла в них, то она либо слишком тусклая, либо плохо различима внутри своего звездного окружения. Либо же с ней связаны еще какие-то трудности. Поэтому предполагать, что подобная звезда может быть надежно отождествлена со звездой из Альмагеста, и была хорошо измерена "в древности", - вряд ли имеет смысл.
В итоге указанного отбора у нас возник список из видимых невооруженным глазом, "быстрых" звезд современного каталога, имеющих отождествления со звездами из Альмагеста. Естественно, надежность этих отождествлений надо еще отдельно проверять. Этим мы займемся позже.
Составленный нами список видимых невооруженным глазом "быстрых" звезд приведен в табл.П1.1 Приложения 1.
Второй список звезд мы назовем списком именных звезд. Он содержится в табл.П1.2 и табл.П1.3. В табл.П1.2 звезды упорядочены по именам, а в табл.П1.3 - по номерам из каталога ярких звезд [1197]. В этот список вошли все звезды, о которых в каталоге ярких звезд BS4 [1197] сказано, что они имеют или имели ранее собственные имена. Таковы, например, Арктур, Альдебаран, Сириус и др.
Списки быстрых и именных звезд имеют некоторые пересечения. Дело в том, что одна и та же звезда может иметь заметное собственное движение и одновременно иметь собственное имя. Именно такие звезды окажутся наиболее полезными для датировки Альмагеста.
5. РАСЧЕТ ЗВЕЗДНОГО НЕБА "В ПРОШЛОЕ". РАСЧЕТНЫЕ КАТАЛОГИ K(t). ФОРМУЛЫ НЬЮКОМБА-КИНОШИТЫ.
5.1. НЕОБХОДИМЫЕ ФОРМУЛЫ.
Имея в своем распоряжении данные о координатах и собственных скоростях звезд современного нам неба, мы можем составить достаточно точный звездный каталог на произвольную эпоху в прошлом. Говоря "достаточно точный", мы имеем в виду, что эта точность соответствует современным астрономическим теориям. Для наших целей этого вполне достаточно. Такую точность можно считать абсолютной по сравнению с точностью старых каталогов.
Расчет положений звезд в прошлом нам пришлось проделать многократно для различных эпох. Для этого мы сначала рассчитывали положения звезд на небесной сфере в году t в координатах α1900, δ1900. Затем мы пересчитывали эти координаты в эклиптикальные координаты lt, bt на эпоху t.
Приведем необходимые формулы, позволяющие пересчитать координаты αs, δs в координаты ls0, bs0 для любых эпох s, s0. Эти формулы учитывают прецессию и собственные движения звезд. Указанные формулы, а также рис.1.5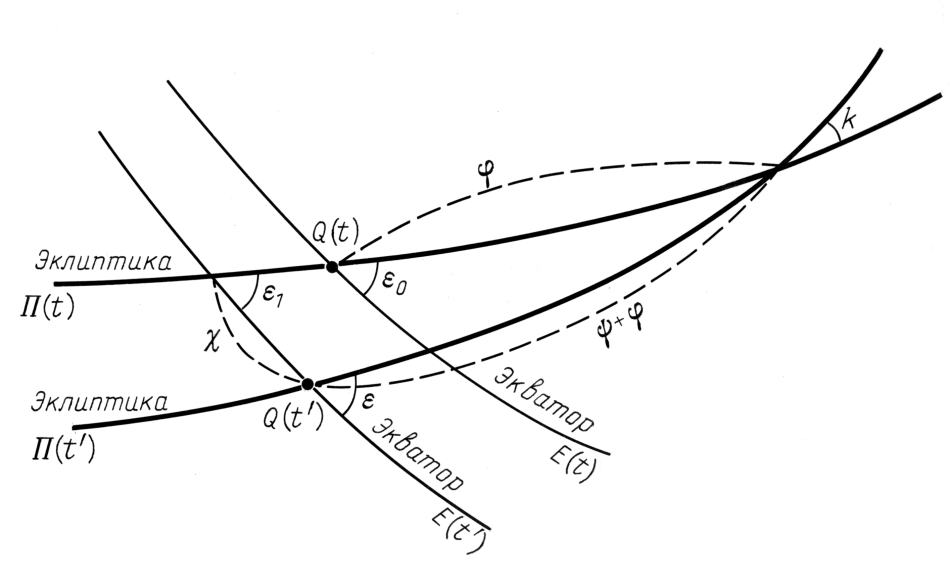
, иллюстрирующий их, заимствованы нами из [1222]. Они получены на основе теории Ньюкомба, модифицированной Киношитой. Сам же пересчет координат описан в следующем пункте 5.2. В этих формулах моменты времени s0 и s отсчитываются от эпохи 2000 года н.э. в юлианских веках, а θ = s0 -s. См. рис.1.5.
Отметим, впрочем, что расхождение между выводами из теории самого Ньюкомба и из ее модификации Киношитой [1222], использованной нами, для наших целей не имеет никакого значения. Для любого момента времени t из рассматриваемого нами исторического интервала, от 600 года до н.э. до 1900 года н.э. разница в эклиптикальных координатах звезды, рассчитанных по теории Ньюкомба и по ее модификации [1222], пренебрежимо мала по сравнению с ошибками Альмагеста. Мы воспользовались [1222], поскольку там формулы для учета прецессии приведены в виде, удобном для вычислений на компьютере.
5.2. АЛГОРИТМ РАСЧЕТА ПОЛОЖЕНИЙ ЗВЕЗД В ПРОШЛОЕ.
Опишем подробно алгоритм расчета звездного каталога K(t), достаточно точно отражающего, согласно теории Ньюкомба, состояние звездного неба в году t. Здесь t-- произвольная эпоха из рассматриваемого нами исторического промежутка, а именно, от 600 года до н.э. до 1900 года н.э. Эпоха t отсчитывается от эпохи 1900 года в юлианских веках в прошлое, то есть, t=1 соответствует эпохе 1800 года, t=10 отвечает эпохе 900 года н.э., t=18 отвечает эпохе 100 года н.э. и т.д. Разница в несколько дней, набегающая из-за различия между юлианским и григорианским календарями и приводящая к тому, что, скажем, эпоха 100 года н.э. в нашем понимании не совпадает с эпохой 1 января 100 года н.э., здесь для нас абсолютно несущественна.
Расчетные звездные каталоги K(t) будут служить нам для сравнения с исследуемым старым каталогом, -- например, с Альмагестом, -- при различных значениях t. Здесь t каждый раз будет иметь смысл произвольной предполагаемой датировки старого каталога. Поэтому расчетные каталоги K(t) должны быть даны в эклиптикальных координатах на эпоху t. Как отмечалось, именно в эклиптикальных координатах составлены все известные старые каталоги, например, Птолемея, ас-Суфи, Улугбека, Коперника, Тихо Браге.
Итак, пусть в современном каталоге, скажем в [1197], звезда имеет экваториальные координаты α0= α19000, δ0= δ19000. Эти координаты отражают положение данной звезды в 1900 году н.э. в сферической системе координат, экватором которой является земной экватор на 1900 год. Экватор задается плоскостью, ортогональной оси вращения Земли. Эта плоскость, напомним, меняется со временем. Нам требуется определить координаты lt, bt, то есть сферические координаты, экватором которых служит эклиптика -- плоскость вращения Земли вокруг Солнца -- эпохи t. Для этого достаточно выполнить следующие действия.
ШАГ 1. Нужно рассчитать координаты α0(t), δ0(t) звезды на момент времени t в экваториальной системе координат эпохи 1900 года. Напомним, что из-за собственных движений звезд, их положения на небе относительно любой фиксированной системы координат меняются со временем. Требуемый расчет положения звезды делается исходя из известных скоростей собственного движения vα, vδ звезды по каждой из координат α1900, δ1900. См. столбцы 5 и 6 табл.4.1 в главе 4. Для неприведенных скоростей собственного движения имеем
α0(t)= α19000(t) = α0 - vα · t, δ0(t)= δ19000(t) = δ0 - vδ · t.
Действительно, как было отмечено выше, в пределах рассматриваемого нами интервала времени, собственное движение звезд по каждой из координат α1900, δ1900 можно считать равномерным. Знак минус в приведенных формулах возникает из-за того, что мы отсчитываем время в прошлое, а знаки скоростей vα, vδ соответствуют естественному течению времени.
Прежде чем практически применять эту формулу, надо привести все входящие величины в одну систему измерений. Скажем, можно измерять α0(t), δ0(t) в радианах, а скорости vα, vδ - в рад/год · 10-2.
ШАГ 2. Нужно перейти от координат α1900, δ1900 к координатам l1900, b1900. После этого мы получаем координаты l0(t), b0(t) нашей звезды на момент времени t в сферических координатах, связанных с эклиптикой эпохи 1900 года. Имеем:
sin b0(t) = -sin α0(t) cos δ0(t) sin ε0 + sin δ0(t)cos ε0,
sin α0(t) cos δ0(t) cos ε0 + sin δ0(t)sin ε0
tan l0(t) = --------------------------------------------------------
cos α0(t) cos δ0(t),
ε0 = 23o 27' 8,26'' .
Эти формулы позволяют однозначно восстановить значения β0(t) и α0(t), поскольку -90o < b0(t) < 90o и l0(t) - α0(t) ≤ 90o. Величина ε0 -- это угол наклона эклиптики 1900 года к экватору 1900 года. См. формулу (1.5.3), в которой, чтобы перейти от 2000 года н.э. к 1900 году н.э., надо положить s0=-1.
ШАГ 3. Нужно перейти от координат l1900, b1900 к вспомогательным координатам l1, b1, которые также связаны с эклиптикой 1900 года. Но точка отсчета долгот для них другая, а именно, совпадает с точкой пересечения эклиптики 1900 года и эклиптики эпохи t, то есть π1900 и π(t).
Этот переход осуществляется по формуламl1(t) = l0(t) - φ,
b1(t) = b0(t),
φ = 173o 57' 38,436'' + 870,0798'' t+ 0,024578'' t2.
Дуга φ между точкой весеннего равноденствия 1900 года на эклиптике π1900 и точкой пересечения π1900 и π(t) получается по формуле (1.5.1), если положить s0=-1 и θ=-t. Тогда эклиптика π(s0) на рис.1.5 будет соответствовать эклиптике π1900. При этом эклиптика π(s) на рис.1.5 будет изображать эклиптику интересующей нас эпохи t. Действительно, время t отсчитывается в столетиях от 1900 года н.э. назад, а разность θ=s-s0 отсчитывается в столетиях от эпохи s0 вперед. Поскольку мы взяли s0=-1, что соответствует 1900 году н.э. (2000-100=1900), то необходимо выбрать θ=-t, чтобы в формуле (1.5.1) эпоха s=s0+ θ соответствовала бы интересующей нас эпохе t.
ШАГ 4. Затем следует перейти от координат l1, b1 к координатам l2, b2. Это -- сферические координаты, связанные с эклиптикой π(t) и отличающиеся от эклиптикальных координат lt, bt лишь выбором точки отсчета долгот. В координатах l2, b2 такой точкой является все та же точка пересечения эклиптик π1900 и π(t). Формулы перехода от l1, b1 к l2, b2 совпадают с формулами (1.5.5). Но только вместо ε0 надо взять угол ε1 между эклиптиками π(t) и π1900:
ε1=- 47,0706''t - 0,033769'' t2 - 0,000050''t3. Это выражение получается из формулы (1.5.2) при s=-1 и θ=-t.
ШАГ 5. Наконец, надо перейти от координат l2, b2 к эклиптикальным координатам lt, bt. Переход осуществляется по формулам
lt=l2 + φ + Ψ, bt=b2,
где φ определено в (1.5.6), а Ψ задается формулой (1.5.4) при s0=-1, θ=-t, то есть
Ψ = -5026,872'' t + 1,1314'' t2 + 0,0001'' t3.
Последовательность описанных выше шагов 1--5 иллюстрируется на рис.1.6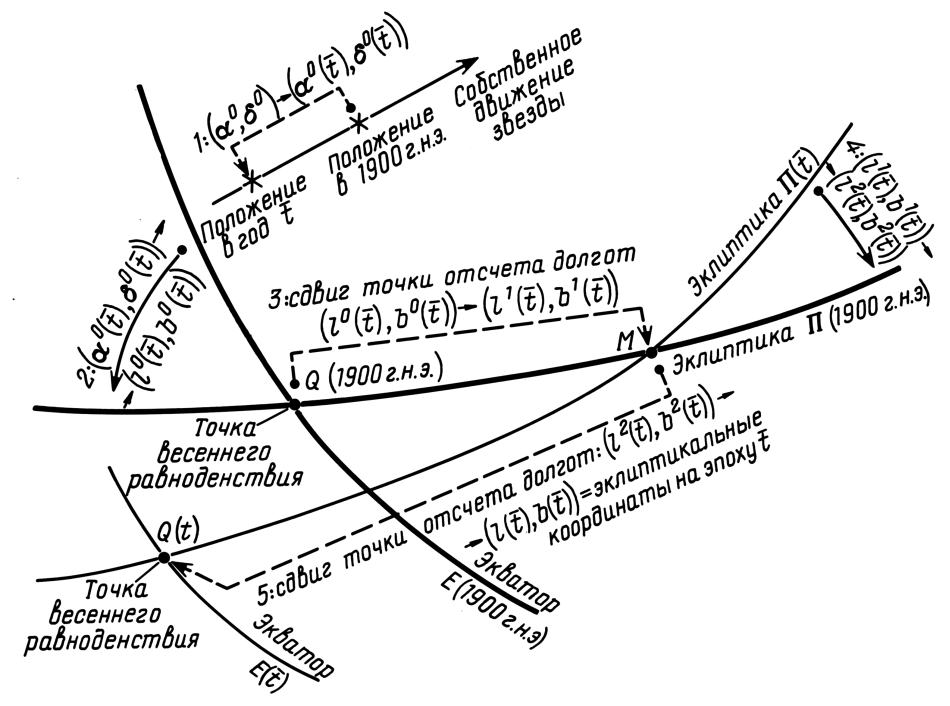
.
Заметим в заключение, что все расчеты, необходимые для датировки звездного каталога, можно провести и без учета теории Ньюкомба-Киношиты. Подробнее об этом мы скажем ниже. Теория Ньюкомба-Киношиты используется нами здесь лишь для получения вспомогательной информации относительно сделанной составителем каталога погрешности в определении плоскости эклиптики. Значение этой погрешности является дополнительным фактором, по которому можно судить о правильности наших выводов. См. главы 6 и 7.
