А.Т.ФОМЕНКО
МАТЕМАТИКА И МИФ СКВОЗЬ ПРИЗМУ ГЕОМЕТРИИ

3. ОБРАЗЫ В МАТЕМАТИЧЕСКОМ АНАЛИЗЕ

МАТЕМАТИКА:
КРИТИЧЕСКИЕ НЕВЫРОЖДЕННЫЕ МНОГООБРАЗИЯ ГЛАДКИХ ФУНКЦИЙ

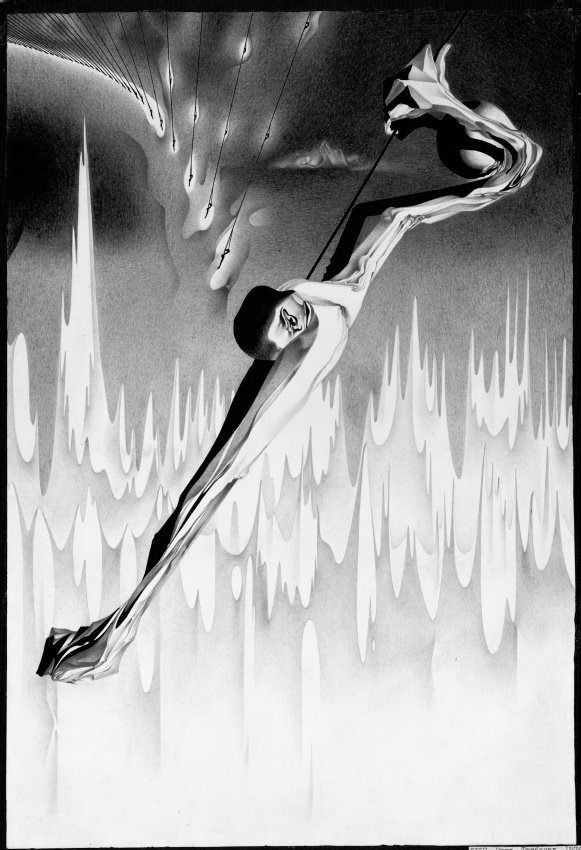
Если на трехмерном пространстве задана функция, критические точки которой заполняют окружность (критическую окружность), то может случиться, что по нормали к окружности второй дифференциал функции невырожден. Такие функции иногда называют боттовскими. Часто бывает полезно изучать так называемую сепаратрисную диаграмму, то есть множество интегральных траекторий градиентного поля функции, входящих в критическую окружность или исходящих из нее. На рисунке условно изображена одна из таких сепаратрисных диаграмм. А именно, для критической окружности индекса 1. При этом сама критическая окружность не нарисована (в действительности она зажата между двумя лентами-диаграммами). Входящая (или исходящая) диаграмма гомеоморфна либо кольцу, разрезанному вдоль его оси критической окружностью, либо листу Мебиуса (также разрезанному вдоль его оси).

МИФОЛОГИЯ
Скандинавские мифы. Наказание А'льбериха. Две бесконечные, сжимающиеся и наточенные как бритвы золотые ленты. Известное "проклятие Альбериха", посланное им вслед украденному у него золотому кольцу - кольцу Нибелунга. Это проклятие в конце концов возвращается к Нибелунгу как бумеранг. Происхождение имени Нибелунга неясно. Согласно одной из версий, в основе лежит nebulones = туманные (немецкое Nebel - туман). Считалось, что Нибелунги - жители гор, подземелий, мрака и туманов. Не очень ясна также принадлежность клада, охраняемого Нибелунгами. По некоторым версиям эти сокровища принадлежат светлым богам, а по другим - самим Нибелунгам.

МАТЕМАТИКА:
ПОВЕРХНОСТЬ УРОВНЯ СЛОЖНОЙ ГЛАДКОЙ ФУНКЦИИ

Поверхность уровня функции - это множество точек, где значение функции равно некоторой фиксированной постоянной. Изображенная поверхность имеет много особых точек. Они расположены, в основном, на концах острых "клювов", вырастающих из поверхности. Замечательно, что весь этот хаос особенностей может появиться даже в том случае, когда исходная функция является полиномом. Правда, в таком случае он должен иметь достаточно большую степень.

МИФОЛОГИЯ.
Скандинавские средневековые мифы. Храм богини земли Эрды, высеченный из монолитной скалы. Богослужение перед храмом, воспроизводящем корни мирового древа. У этих корней живут норны - богини судьбы, прорицательницы. В <<Прорицании ве"львы>> пророчица вспоминает девять миров. У корней мирового древа живет змей Нидхегг. Выше поднимается ствол, на вершине которого - орел, а на среднем уровне - четыре оленя, поедающие листья дерева жизни. Предсказательницы-норны определяют судьбы богов. Перед концом мира бог О'дин спускается в подземное царство и, пробудив ве"льву от сна, вынуждает ее дать пророчество о судьбе богов. Богиня сообщает ему о грядущей катастрофе, приводя О'дина в оцепенение и снова погружается в небытие.

МАТЕМАТИКА:
ФУНКЦИИ МОРСА И ТЕОРЕМА ОБ ЭЙЛЕРОВОЙ ХАРАКТЕРИСТИКЕ

Показан типичный график гладкой функции, все критические точки которой невырождены. Такие функции называются функциями Морса. Эти функции типичны в пространстве всех гладких функций. А именно, любая гладкая функция путем сколь угодно малой деформации может быть превращена в функцию Морса. Критические точки различаются по их типам: минимумы, максимумы и седла (седловые точки). Все эти типы точек можно увидеть, изучая фотографию горного пейзажа. Пики гор - это максимумы функции, впадины - это минимумы, а горные перевалы - это се'дла.  Количество и тип критических точек функции в значительной мере определяет топологию того пространства, на котором функция задана. Изучение этой связи составляет предмет теории Морса. Зритель видит горный рельеф острова в океане. Рельеф может быть сколь угодно сложен. Предположим, для простоты, что на берегу океана нет критических точек функции, т.е. что прибой превратил прибрежную полосу суши в наклонную поверхность, сгладив на ней все выпуклости и заполнив песком все впадины.  Вычислим число A горных пиков на острове (т.е. максимумов функции высоты), число B впадин (т.е. минимумов) и число C перевалов (т.е. седел).  Построим число A-С+В. Оно называется эйлеровой характеристикой поверхности. Оказывается, для любого острова, гомеоморфного кругу (т.е. такого, внутри которого нет лагун, озер), это число всегда равно 1.

МИФОЛОГИЯ.
Извержение вулкана - настолько впечатляющее зрелище, что древний человек естественно обожествил это грозное явление природы. Мифы северных народов вспоминают о сотворении мира в результате извержения подводного вулкана, зародившегося в недрах мирового океана, скованного толстым неподвижным льдом.  Пламя взломало лед, осветило вселенную и из-под воды поднялась земля.

МАТЕМАТИКА:
ГРАФИК НЕПРЕРЫВНОЙ, НО НЕ ГЛАДКОЙ ФУНКЦИИ

Изображен график непрерывной функции от двух переменных, имеющей много точек, где производная стремится к бесконечности. Они отвечают вершинам острых пиков. Такая функция почти всюду дифференцируема, хотя имеет "очень много" точек, где дифференцируемости нет. Оказывается, число "плохих" точек можно увеличивать так, что "в пределе" получится непрерывная функция, которая ни в одной точке не дифференцируема. Открытие таких непрерывных, но нигде не дифференцируемых функций произвело в XIX веке большое впечатление на математиков.

МИФОЛОГИЯ.
Средневековые европейские легенды о чистилище.
Одна из версий гласила, что души умерших, попав в чистилище, подвешиваются на веревках-качелях и долгое время раскачиваются над бесконечным океаном огня. Пламя выжигает из душ все нечистое. Чем больше грешил человек в своей земной жизни, тем дольше его душа раскачивается над огнем. Дж.Фрэзер отмечал, что в народных обычаях, связанных с праздниками огня, есть черты, указывающие на существование в Европе в прежние времена практики человеческих жертвоприношений. Живые люди часто играли роль олицетворений духа дерева и духа хлеба. В этом качестве они предавались смерти. В праздниках огня инсценировка сожжения людей заходит иногда так далеко, что есть основания рассматривать ее как пережиток более древнего обычая, требовавшего их действительного сожжения.(Дж.Дж.Фрэзер. Золотая ветвь).

МАТЕМАТИКА:
ПРАВИЛЬНЫЕ ФУНКЦИИ МОРСА НА ТРЕХМЕРНЫХ МНОГООБРАЗИЯХ

Сепаратрисную диаграмму седловой критической точки функции Морса на трехмерном многообразии можно изобразить в виде "колокола". Критические точки функции могут распределяться по многообразию довольно хаотично. Однако, каждую функцию Морса можно гладко продеформировать (в классе функций Морса) в так называемую правильную функцию. Функция Морса называется правильной, если все ее критические точки одного индекса лежат на одной поверхности уровня функции. Для трехмерных многообразий это означает, что имеется не более четырех различных критических уровней функции. Сначала идут минимумы, потом - седла индекса 1, затем - седла индекса 2, и наконец - максимумы функции. Зритель видит один из таких уровней функции, на котором сосредоточены все ее критические точки индекса 2. Рисунок условен в том смысле, что внутри трехмерного евклидова пространства невозможно точно изобразить тот факт, что двумерный сепаратрисный диск должен "опускаться вниз", а одномерный сепаратрисный отрезок должен "подниматься вверх" и быть при этом ортогонален (трансверсален) 2-диску.

МИФОЛОГИЯ.
В некоторых средневековых европейских мифах обыгрывался образ колоколов, подвешенных в пространстве на бесконечных канатах. Каждый колокол отвечал за судьбу какого-то человека. Под тяжестью человеческих грехов колокол постепенно опускался вниз, а колокол праведника наоборот поднимался все выше и выше, к раю. В день страшного суда все они зазвонят. "Чистые" колокола - высоким тоном, а "грязные" - низким. Эти звуки сольются в единую божественную мелодию.  Представление о том, что жизнь человека (и его судьба) подвешена на тонкой нити, возникло в христианском средневековом богословии. Нить можно легко перерезать.  Средневековые специалисты изучали также вопрос - кому позволено резать нить. Например, может ли обрезать нить жизни не тот, кто подвесил душу на нити.

МАТЕМАТИКА:
ДЕФОРМАЦИЯ РИМАНОВОЙ ПОВЕРХНОСТИ АЛГЕБРАИЧЕСКОЙ ФУНКЦИИ.

Изображена "трехмерная модель" деформации римановой поверхности алгебраической функции w=[(z-a)(z-b)(z-c)(z-d)]^(1/2) в четырехмерном евклидовом пространстве. Риманова поверхность такой функции гомеоморфна двумерной сфере с одной ручкой, т.е.  двумерному тору (при условии, что все корни a, b, c, d полинома степени 4 различны). Для построения римановой поверхности нужно взять два экземпляра двумерной сферы, на каждом из которых сделано по два разреза, и склеить (отождествить) соответствующие берега разрезов. В результате получится тор, представленный как две сферы, соединенные двумя трубками-цилиндрами. Такова картина в случае, когда все 4 корня простые, т.е. не кратные. Если же полином начинает деформироваться таким образом, что его корни стремятся слиться (т.е. когда в пределе получаются кратные корни), то риманова поверхность также реагирует на эту деформацию. Она начинает деформироваться таким образом, что на ней появляются исчезающие циклы, возникают особые точки и в результате риманова поверхность перестает быть гладкой. Пример такой деформации и показан нами.

МИФОЛОГИЯ.
Многорукий Шива - один из центральных богов индийского пантеона. Ему отведена роль уничтожителя мира и богов в конце каждого временно'го периода (кальпы). Посредине лба Шивы - третий глаз, появившийся у него, когда жена Парвати, подойдя сзади, закрыла ладонями два других глаза Шивы. Этот глаз особенно губителен. Его пламенем он сжег бога любви Каму, когда тот попытался отвлечь его от аскетических подвигов. Шива обычно изображается с многими головами и многими руками. В качестве "великого аскета" он, голый, с телом, покрытым золой, со вставшими копной волосами, с серьгами из змей и ожерельем из черепов, восседает на тигровой шкуре и погружен в медитацию. Культ Шивы содержит устрашающие черты. Его свита - это злые духи и оборотни. В пуранах перечисляются 1008 имен или эпитетов Шивы. В японской буддийской мифологии - популярная тысячерукая Каннон. Поздние ее скульптуры имели по 20 рук справа и слева, не считая двух главных.